ГДЗ по Алгебре 10 Класс Номер 16.51 Профильный Уровень Мордкович — Подробные Ответы

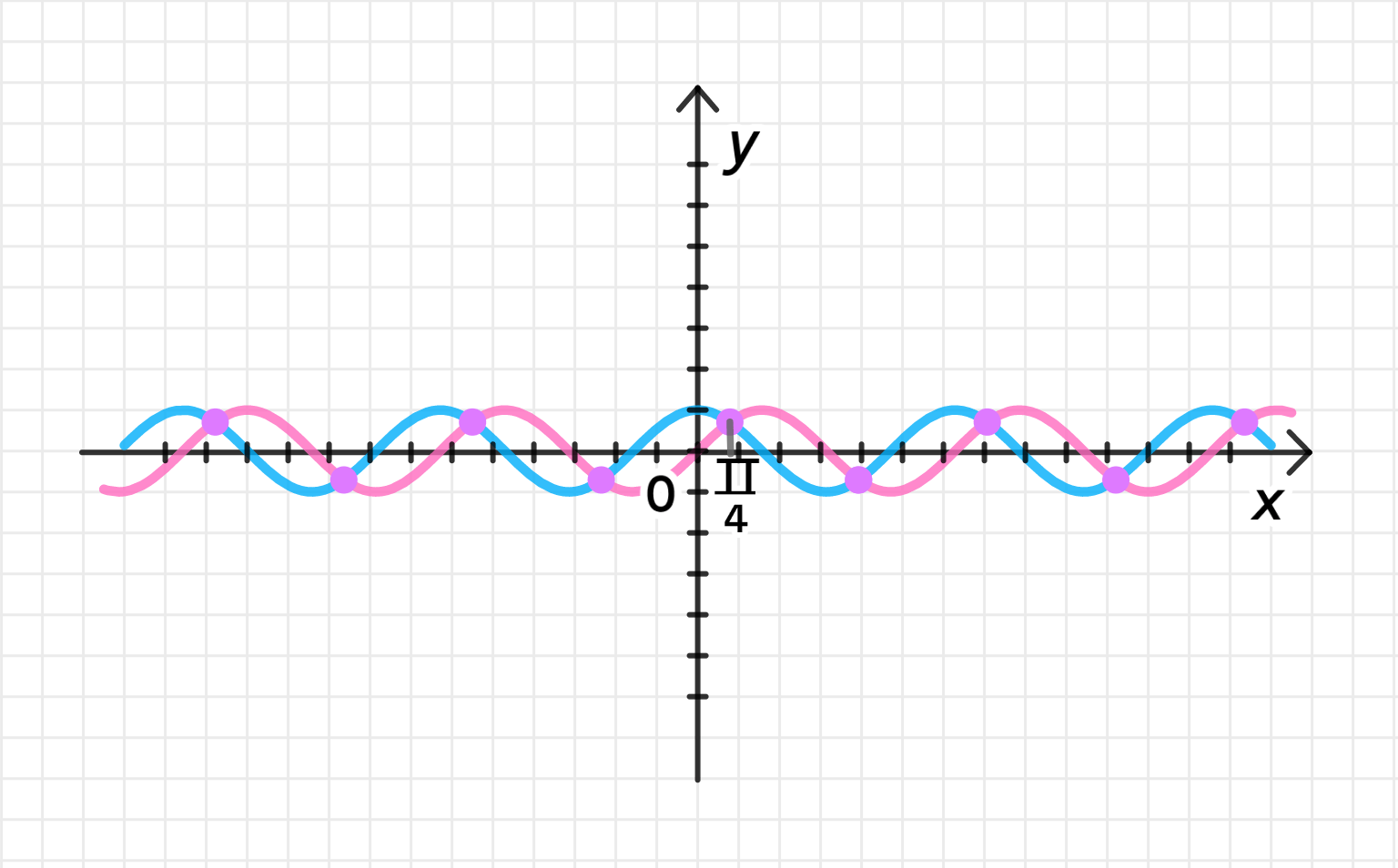
Решите графически уравнение:

а) sinx — cosx;

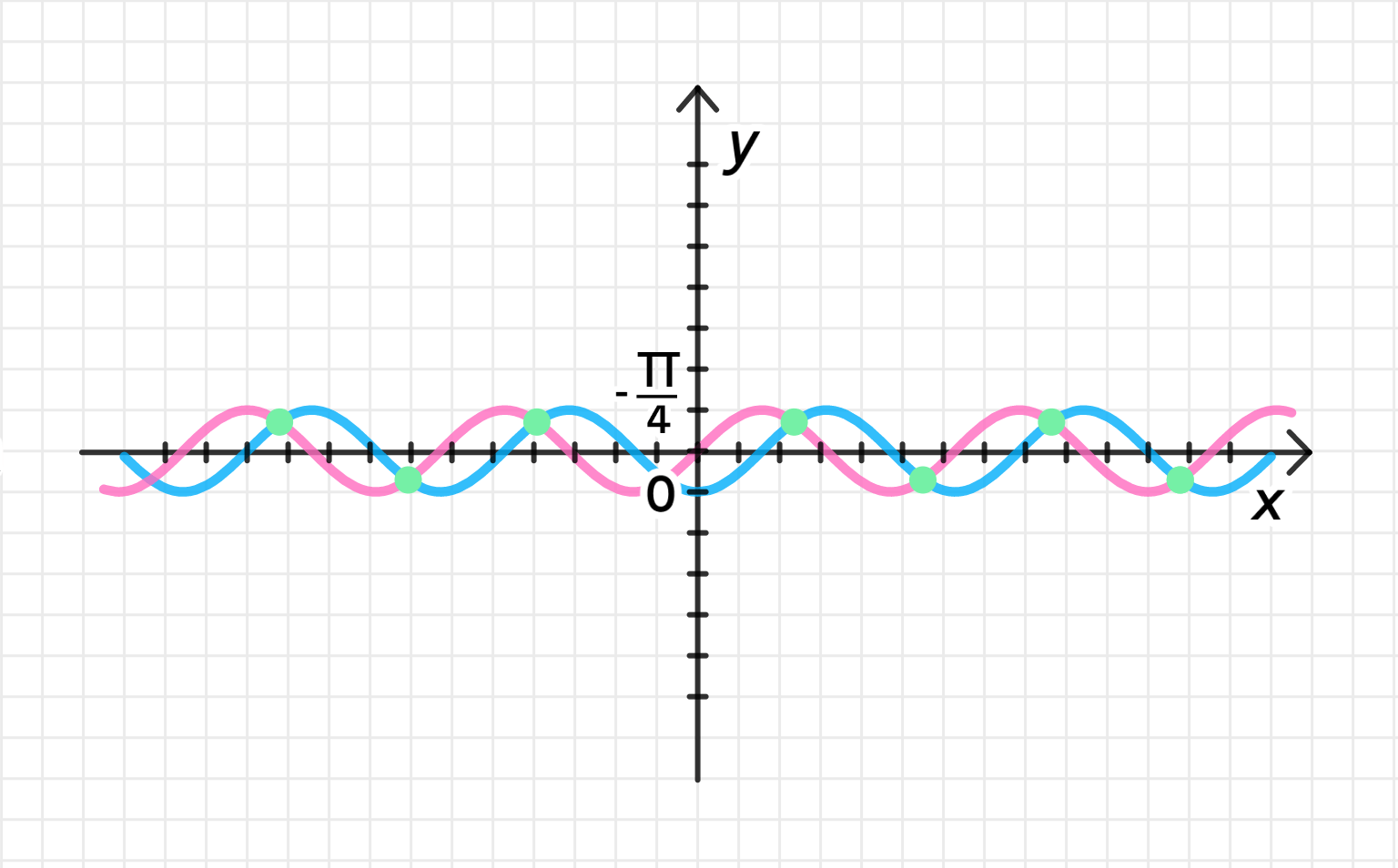
б) sinx + cosx = 0.

а) $\sin x = \cos x$;

Построим графики функций $y = \sin x$ и $y = \cos x$:

Графики пересекаются в точке:

$$x_1 = \frac{\pi}{6} + \frac{1}{2} \cdot \frac{\pi}{6} = \frac{2\pi}{12} + \frac{\pi}{12} = \frac{3\pi}{12} = \frac{\pi}{4};$$

Расстояние между соседними точками пересечения равно $\pi$;

Ответ: $x = \frac{\pi}{4} + \pi n$.

б) $\sin x + \cos x = 0$;

Преобразуем уравнение:

$$\sin x = -\cos x;$$

Построим графики функций $y = \sin x$ и $y = \cos x$;

Отразим график функции $y = \cos x$ относительно оси $Ox$:

Графики пересекаются в точке:

$$x_1 = \frac{\pi}{6} — \frac{1}{2} \cdot \frac{\pi}{6} = \frac{-2\pi}{12} — \frac{\pi}{12} = \frac{-3\pi}{12} = -\frac{\pi}{4};$$

Расстояние между соседними точками пересечения равно $\pi$;

Ответ: $x = -\frac{\pi}{4} + \pi n$.

а) $\sin x = \cos x$

Построение графиков функций $y = \sin x$ и $y = \cos x$:

• Графики синуса и косинуса — это периодические функции с периодом $2\pi$.
• График функции $y = \sin x$ начинается в начале координат (при $x = 0$ значение функции равно 0) и колеблется от -1 до 1.
• График функции $y = \cos x$ начинается с максимального значения 1 (при $x = 0$) и тоже колеблется от -1 до 1.

Эти функции имеют одинаковый период, но сдвиг фазы: синус «отстает» от косинуса на $\frac{\pi}{2}$.

Таким образом, оба графика будут пересекаться в точках, где их значения равны друг другу.

Поиск точек пересечения:

Мы ищем решения уравнения:

$$\sin x = \cos x.$$

Для этого можно воспользоваться известным тригонометрическим тождеством:

$$\sin x = \cos x \implies \tan x = 1.$$

Уравнение $\tan x = 1$ имеет решения:

$$x = \frac{\pi}{4} + n\pi, \quad n \in \mathbb{Z},$$

где $n$ — целое число. Это означает, что графики пересекаются в точках $x = \frac{\pi}{4} + n\pi$.

Расстояние между соседними точками пересечения:

Период функции $\sin x$ или $\cos x$ равен $2\pi$, однако, поскольку точки пересечения следуют с шагом $\pi$, расстояние между соседними точками пересечения равно $\pi$.

Ответ: $x = \frac{\pi}{4} + \pi n$, где $n$ — целое число.

б) $\sin x + \cos x = 0$

Преобразование уравнения:

Мы начинаем с уравнения:

$$\sin x + \cos x = 0.$$

Из этого уравнения можно выразить $\sin x$ через $\cos x$:

$$\sin x = -\cos x.$$

Построение графиков функций $y = \sin x$ и $y = \cos x$:

• График функции $y = \sin x$ — это стандартная синусоида, начинающаяся в начале координат.
• График функции $y = \cos x$ также является синусоидой, но сдвинутой на $\frac{\pi}{2}$ вправо.

Мы ищем точки пересечения этих функций, где $\sin x = -\cos x$.

Отражение графика функции $y = \cos x$ относительно оси $O_x$:

Чтобы упростить решение, можно отразить график функции $y = \cos x$ относительно оси $O_x$, получив график функции $y = -\cos x$. Тогда мы ищем пересечение графика функции $y = \sin x$ и графика функции $y = -\cos x$.

Визуально это будет точка, где синусоида пересекает отраженный график косинуса.

Поиск точек пересечения:

Для решения уравнения $\sin x = -\cos x$ можно снова использовать тождество для тангенса:

$$\sin x = -\cos x \implies \tan x = -1.$$

Уравнение $\tan x = -1$ имеет решения:

$$x = -\frac{\pi}{4} + n\pi, \quad n \in \mathbb{Z}.$$

Это означает, что графики пересекаются в точках $x = -\frac{\pi}{4} + n\pi$.

Расстояние между соседними точками пересечения:

Так как период функции $\sin x$ и $\cos x$ равен $2\pi$, а точки пересечения для этого уравнения следуют с шагом $\pi$, расстояние между соседними точками пересечения также равно $\pi$.

Ответ: $x = -\frac{\pi}{4} + \pi n$, где $n$ — целое число.