Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 16.53 Профильный Уровень Мордкович — Подробные Ответы
Решите неравенство:
а) ;
б)
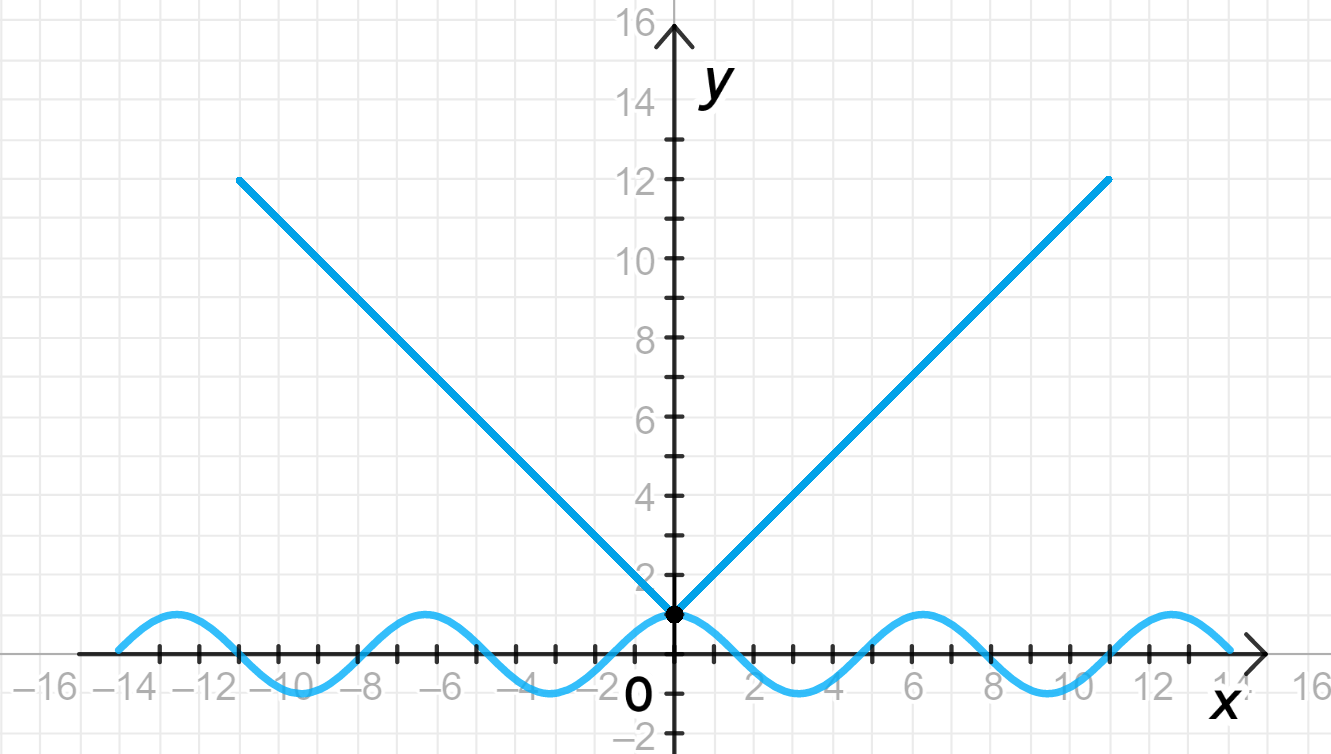
а) ;
— уравнение синусоиды;
— уравнение модуля:
Графики функций:
Ответ: .
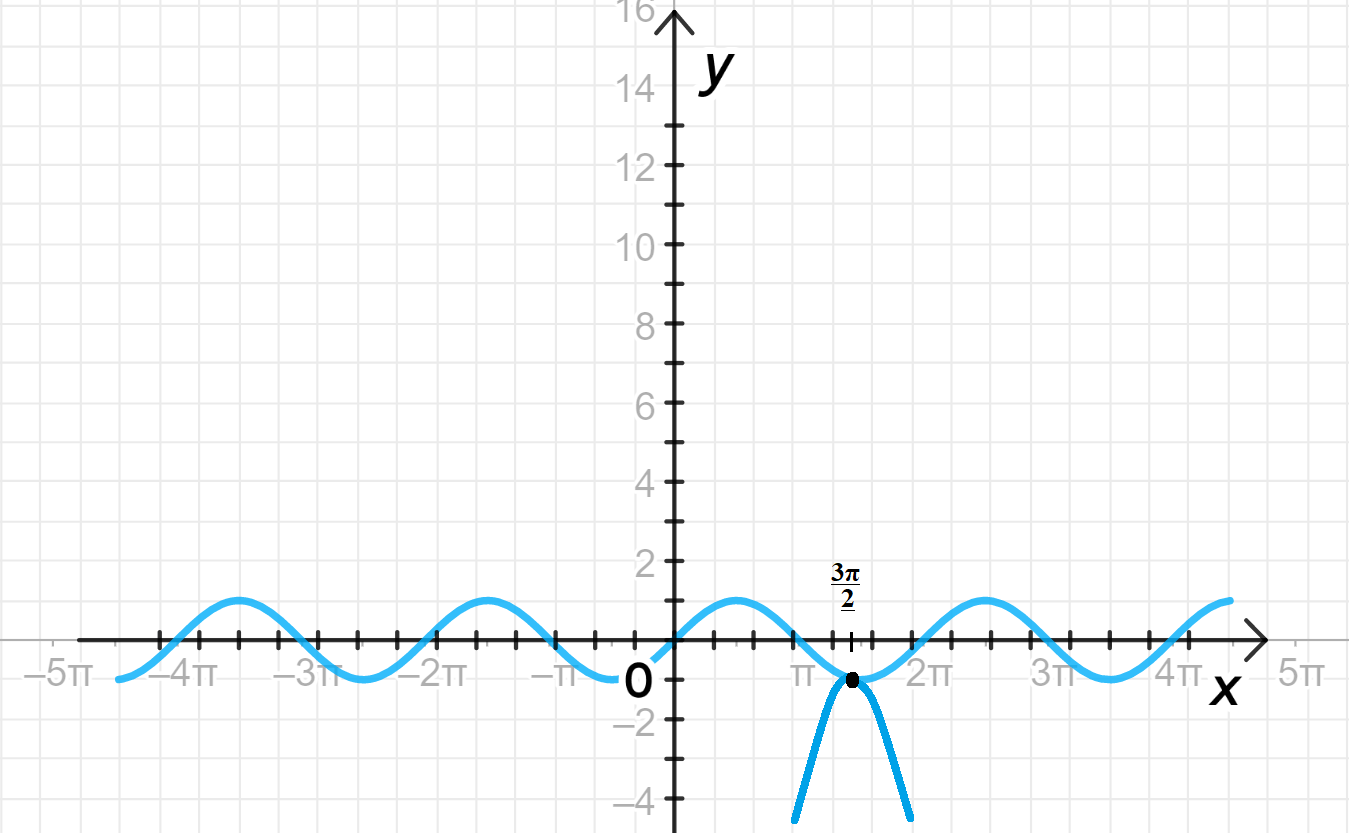
б) ;
— уравнение синусоиды;
— уравнение параболы:
Графики функций:
Ответ: .
а) Условие:
Здесь мы будем рассматривать два уравнения:
- — это уравнение синусоиды.
- — это уравнение модуля, которое представляет собой V-образную функцию.
Шаг 1: Построение графиков функций
- Функция представляет собой стандартную косинусоиду. Ее график колеблется между значениями 1 и -1 с периодом .
- Функция является модификацией линейной функции с углом наклона 1 и симметрична относительно оси . Она начинается с точки и растет как для и для .
Теперь строим таблицу значений для обеих функций для нескольких значений :
Таблица показывает значения функции (в первом столбце) и функции (во втором столбце). Мы видим, что для , , что совпадает с , то есть для обоих выражений.
Шаг 2: Поиск решения неравенства
Теперь нам нужно решить неравенство:
- Для обе функции равны 1, то есть и , следовательно, неравенство выполняется.
- Для других значений , например , мы видим, что , что меньше 2, а значит неравенство уже не выполняется.
Таким образом, единственное решение неравенства — это .
Ответ: .
б) Условие:
Здесь мы работаем с двумя функциями:
- — это уравнение синусоиды.
- — это парабола, переведенная по оси на и с отражением относительно оси .
Шаг 1: Построение графиков функций
- Функция — стандартная синусоида с периодом , амплитудой 1.
- Функция представляет собой параболу, которая смещена на по оси и имеет вершину в точке , с открывающимися вниз ветвями.
Таблица значений для нескольких :
Шаг 2: Поиск решения неравенства
Нам нужно решить неравенство:
- Для , , и также , то есть неравенство выполняется.
- Для других значений , например или , синусоида и парабола дают разные значения, и неравенство не выполняется.
Таким образом, единственное решение — это .
Ответ: .
Итак, после детального разбора обоих случаев, мы пришли к следующим ответам:
- Для неравенства ответ: .
- Для неравенства ответ: .