Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 16.54 Профильный Уровень Мордкович — Подробные Ответы
а) ;
б)
а) ;
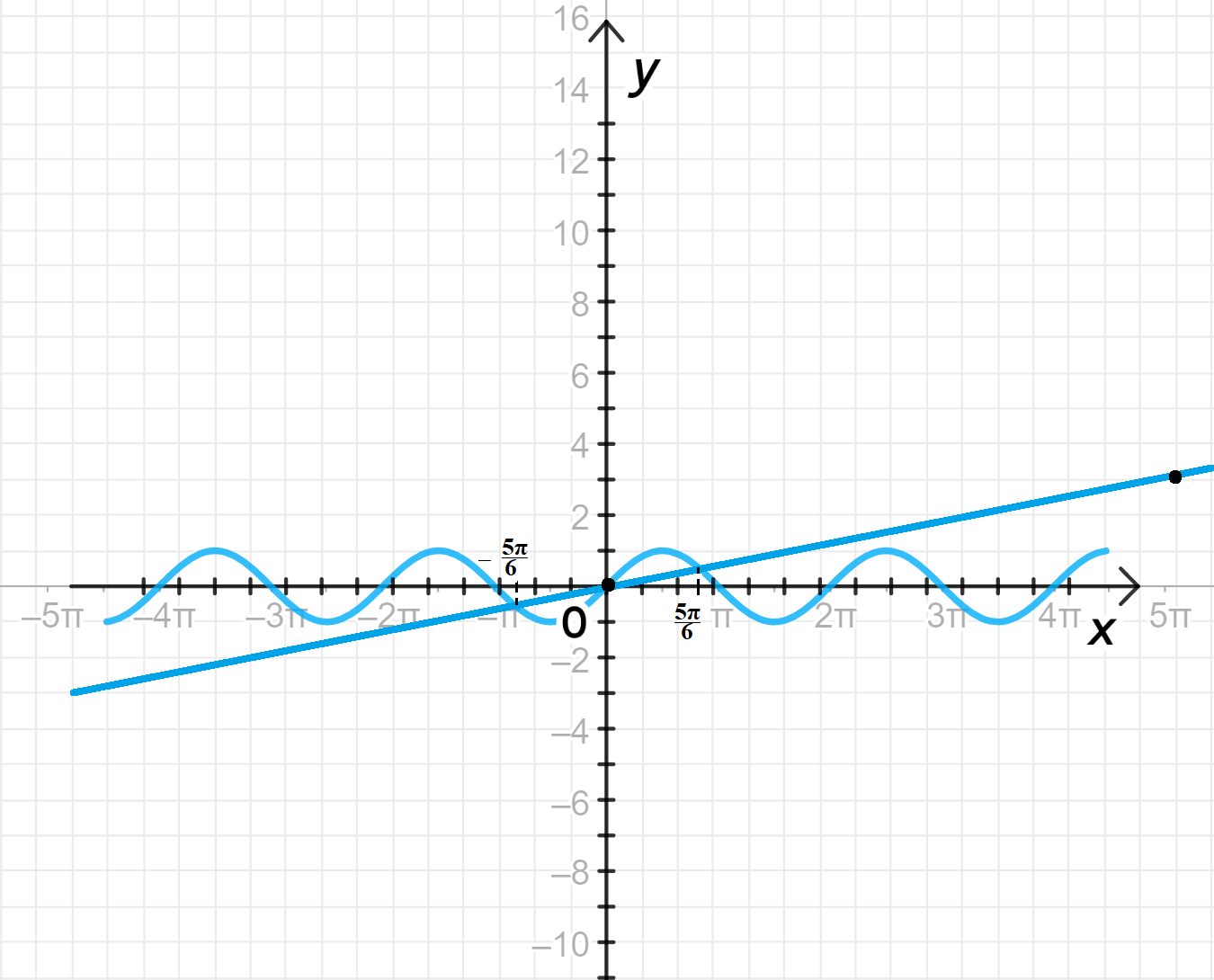
— уравнение синусоиды;
— уравнение прямой:
| 0 | ||
|---|---|---|
| 0 | 0,5 |
Графики функций:
Ответ: .
б) ;
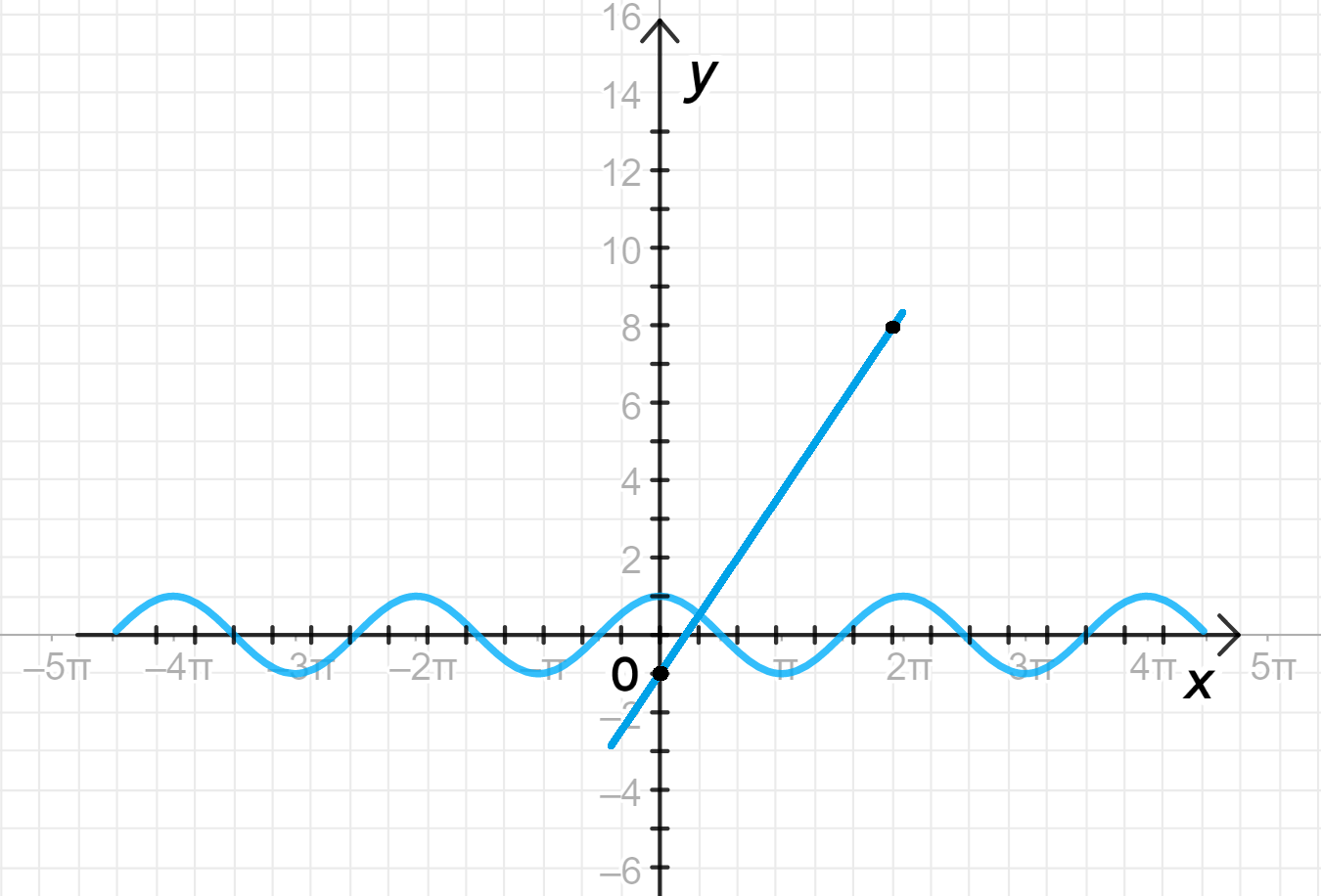
— уравнение синусоиды;
— уравнение прямой:
| 0 | ||
|---|---|---|
| -1 | 2 |
Графики функций:
Ответ: .
а) Условие:
Нам нужно решить неравенство:
Здесь мы будем рассматривать две функции:
- — это уравнение синусоиды.
- — это уравнение прямой, проходящей через начало координат с угловым коэффициентом .
Шаг 1: Построение графиков функций
- Функция представляет собой стандартную синусоиду с периодом и амплитудой 1.
- Функция — это линейная функция с угловым коэффициентом . Это прямая, проходящая через начало координат, с постепенным увеличением значения .
Для того чтобы понять, где происходит пересечение и выполнение неравенства, составим таблицу значений для обеих функций в нескольких точках:
Шаг 2: Описание графиков
- График функции колеблется между -1 и 1.
- График функции — это прямая линия с угловым коэффициентом , которая постепенно увеличивается.
При , обе функции равны нулю. Но для мы видим, что синусоиды и прямая пересекаются, и их значения равны между собой, то есть и .
Шаг 3: Решение неравенства
Чтобы решить неравенство , нам нужно определить, в каких областях синусоида находится выше прямой.
- Для , значения функций равны, поэтому на неравенство не выполняется.
- Для , синусоида будет перемещаться между -1 и 1, а прямая будет расти. Сначала синусоида будет выше прямой, но через некоторое время она опустится ниже прямой. Это также происходит для .
- Поэтому решения неравенства будут в интервалах и .
Ответ: .
б) Условие:
Нам нужно решить неравенство:
Здесь мы будем рассматривать две функции:
- — это уравнение синусоиды.
- — это уравнение прямой.
Шаг 1: Построение графиков функций
- Функция — это стандартная косинусоида с амплитудой 1 и периодом .
- Функция — это прямая, которая начинается с точки на оси и увеличивается с угловым коэффициентом .
Для того чтобы понять, где происходит пересечение и выполнение неравенства, составим таблицу значений для обеих функций в нескольких точках:
Шаг 2: Описание графиков
- График функции будет колебаться между -1 и 1.
- График функции — это прямая линия, которая будет выше оси при больших значениях .
При , , а прямая принимает значение -1, следовательно, неравенство выполняется для .
Шаг 3: Решение неравенства
Чтобы решить неравенство , необходимо понять, в каких областях график синусоиды находится ниже прямой.
- Для , , а прямая равна -1, следовательно, неравенство выполняется.
- Для , , а значение прямой равно 2, и неравенство также выполняется.
- Для более высоких значений синусоида постепенно снижается, а прямая продолжает расти. При прямой будет больше, чем синусоида.
Таким образом, решение неравенства начинается с и продолжается для всех более высоких значений .
Ответ: .
Итак, после детального анализа и построения графиков, мы пришли к следующим результатам:
- Для неравенства ответ: .
- Для неравенства ответ: .