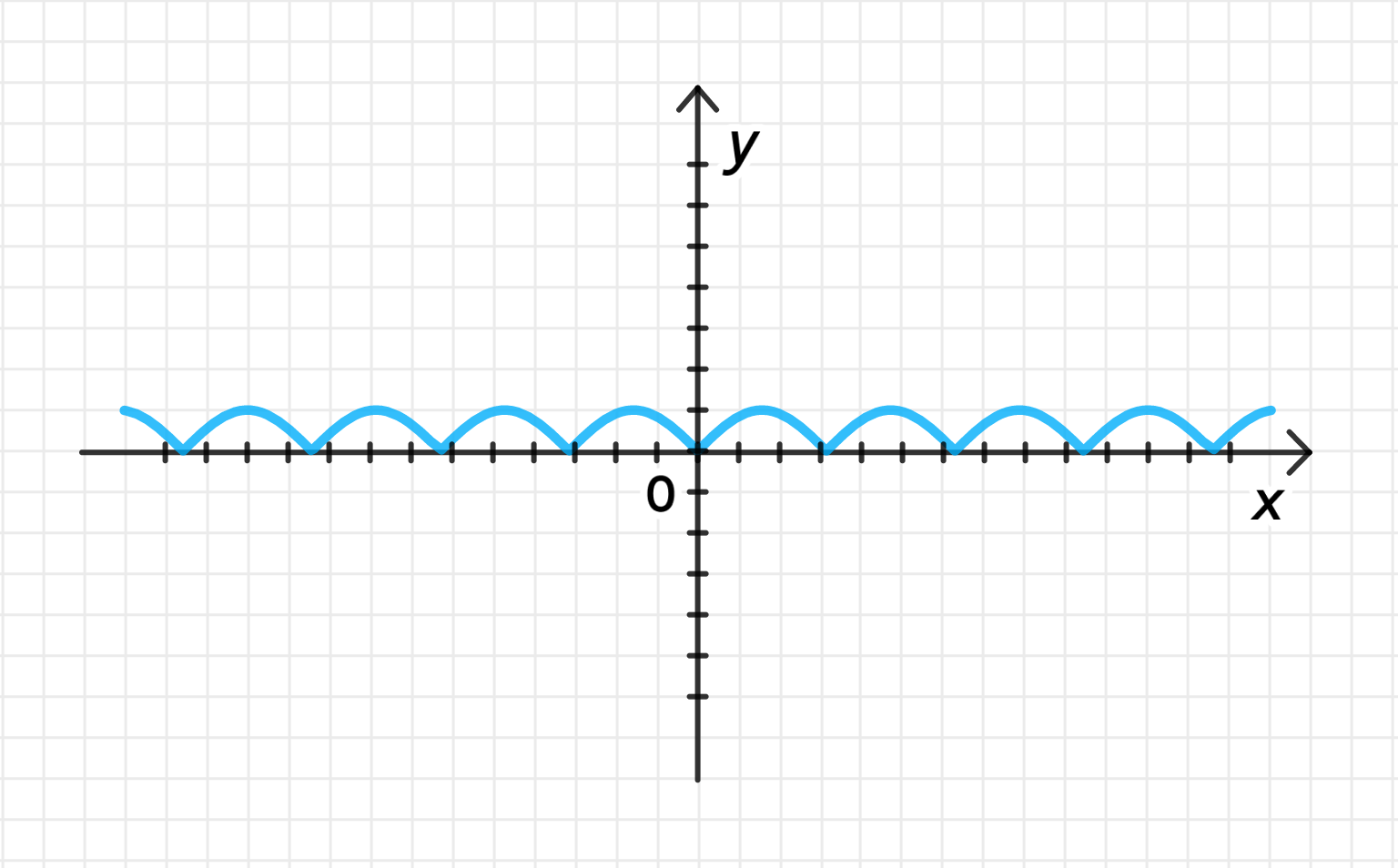ГДЗ по Алгебре 10 Класс Номер 16.55 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\mathrm{\mid }\sin x\mathrm{\mid }$;

б) $y=\mid \cos x-\frac{1}{2}\mid$;

в) $y=\mathrm{\mid }\cos x\mathrm{\mid }$;

г) $y=\mid \sin x+\frac{1}{2}\mid$

а) $y=\mathrm{\mid }\sin x\mathrm{\mid }$;

Построим график функции $y=\sin x$;

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

б) $y=\mid \cos x-\frac{1}{2}\mid$;

Построим график функции $y=\cos x$;

Переместим его на $\frac{1}{2}$ единицы вниз вдоль оси ординат;

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

в) $y=\mathrm{\mid }\cos x\mathrm{\mid }$;

Построим график функции $y=\cos x$;

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

г) $y=\mid \sin x+\frac{1}{2}\mid$;

Построим график функции $y=\sin x$;

Переместим его на $\frac{1}{2}$ единицы вверх вдоль оси ординат;

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

а) $y=\mathrm{\mid }\sin x\mathrm{\mid }$;

Построим график функции $y=\sin x$:

График функции $y=\sin x$ представляет собой волну, которая периодически колеблется вверх и вниз относительно оси $Ox$ с амплитудой 1. Функция $\sin x$ имеет период $2\pi$, то есть, за один период график повторяется.

График функции будет выглядеть следующим образом:

• Когда $x=0$, $\sin 0=0$.
• Когда $x=\frac{\pi }{2}$, $\sin \frac{\pi }{2}=1$ (максимум).
• Когда $x=\pi$, $\sin \pi =0$.
• Когда $x=\frac{3\pi }{2}$, $\sin \frac{3\pi }{2}=-1$ (минимум).
• Когда $x=2\pi$, $\sin 2\pi =0$.

Этот цикл повторяется для всех значений $x$, увеличиваясь или уменьшаясь на $2\pi$ для каждого нового периода.

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

Теперь рассмотрим, что происходит с графиком, если мы применим операцию взятия абсолютного значения $\mathrm{\mid }\sin x\mathrm{\mid }$.

• Все отрицательные значения функции $\sin x$, то есть те части графика, которые находятся ниже оси $Ox$, отразятся относительно оси $Ox$ и будут перенесены вверх.
• Это означает, что все отрицательные значения $\sin x$ (например, на интервале $(\pi ,2\pi )$) будут заменены на положительные, то есть, они будут отражены в верхнюю половину координатной плоскости.

Таким образом, график функции $y=\mathrm{\mid }\sin x\mathrm{\mid }$ будет выглядеть как волна, которая поднимет все негативные колебания и оставит положительные части без изменений.

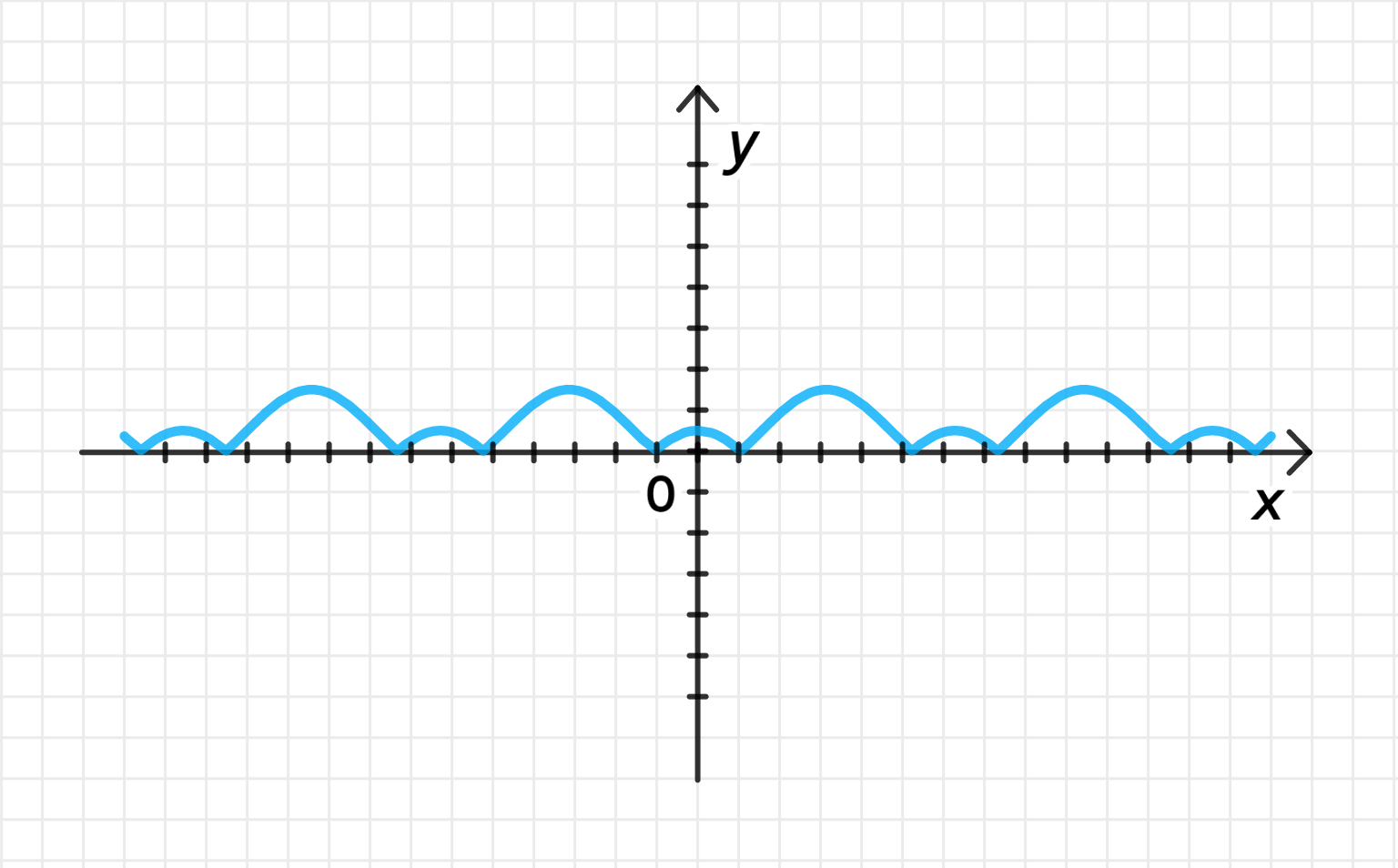
б) $y=\mid \cos x-\frac{1}{2}\mid$;

Построим график функции $y=\cos x$:

График функции $y=\cos x$ также представляет собой волну, но в отличие от синуса, косинус начинается с максимума в точке $x=0$:

• Когда $x=0$, $\cos 0=1$ (максимум).
• Когда $x=\frac{\pi }{2}$, $\cos \frac{\pi }{2}=0$.
• Когда $x=\pi$, $\cos \pi =-1$ (минимум).
• Когда $x=\frac{3\pi }{2}$, $\cos \frac{3\pi }{2}=0$.
• Когда $x=2\pi$, $\cos 2\pi =1$ (максимум).

График повторяется каждые $2\pi$, так как период функции косинуса также составляет $2\pi$.

Переместим его на $\frac{1}{2}$ единицы вниз вдоль оси ординат:

После того как мы построили график $y=\cos x$, мы должны переместить его на $\frac{1}{2}$ единицы вниз. Это означает, что каждый коэффициент функции $y=\cos x$ будет уменьшен на $\frac{1}{2}$, и график будет опущен на эту величину.

Это действие приведет к тому, что значение функции $\cos x$ в каждой точке будет уменьшено на $\frac{1}{2}$. Например:

• Когда $x=0$, $\cos 0-\frac{1}{2}=1-\frac{1}{2}=\frac{1}{2}$.
• Когда $x=\frac{\pi }{2}$, $\cos \frac{\pi }{2}-\frac{1}{2}=0-\frac{1}{2}=-\frac{1}{2}$.
• Когда $x=\pi$, $\cos \pi -\frac{1}{2}=-1-\frac{1}{2}=-\frac{3}{2}$.
• Когда $x=\frac{3\pi }{2}$, $\cos \frac{3\pi }{2}-\frac{1}{2}=0-\frac{1}{2}=-\frac{1}{2}$.
• Когда $x=2\pi$, $\cos 2\pi -\frac{1}{2}=1-\frac{1}{2}=\frac{1}{2}$.

Этот сдвиг вниз сместит все значения функции вниз на половину единицы.

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

После того, как мы сдвинули график вниз, необходимо применить операцию взятия абсолютного значения. То есть все значения, которые находятся ниже оси $Ox$ (отрицательные значения), нужно отразить выше оси $Ox$. Все положительные значения останутся без изменений.

Например:

• Если на участке графика значение функции было отрицательным (например, $y=-\frac{3}{2}$), после отражения оно станет положительным (например, $y=\frac{3}{2}$).

Этот процесс обеспечит, что вся функция $y=\mid \cos x-\frac{1}{2}\mid$ будет положительной, а волны, которые ранее были ниже оси $Ox$, теперь будут отображаться в верхней части графика.

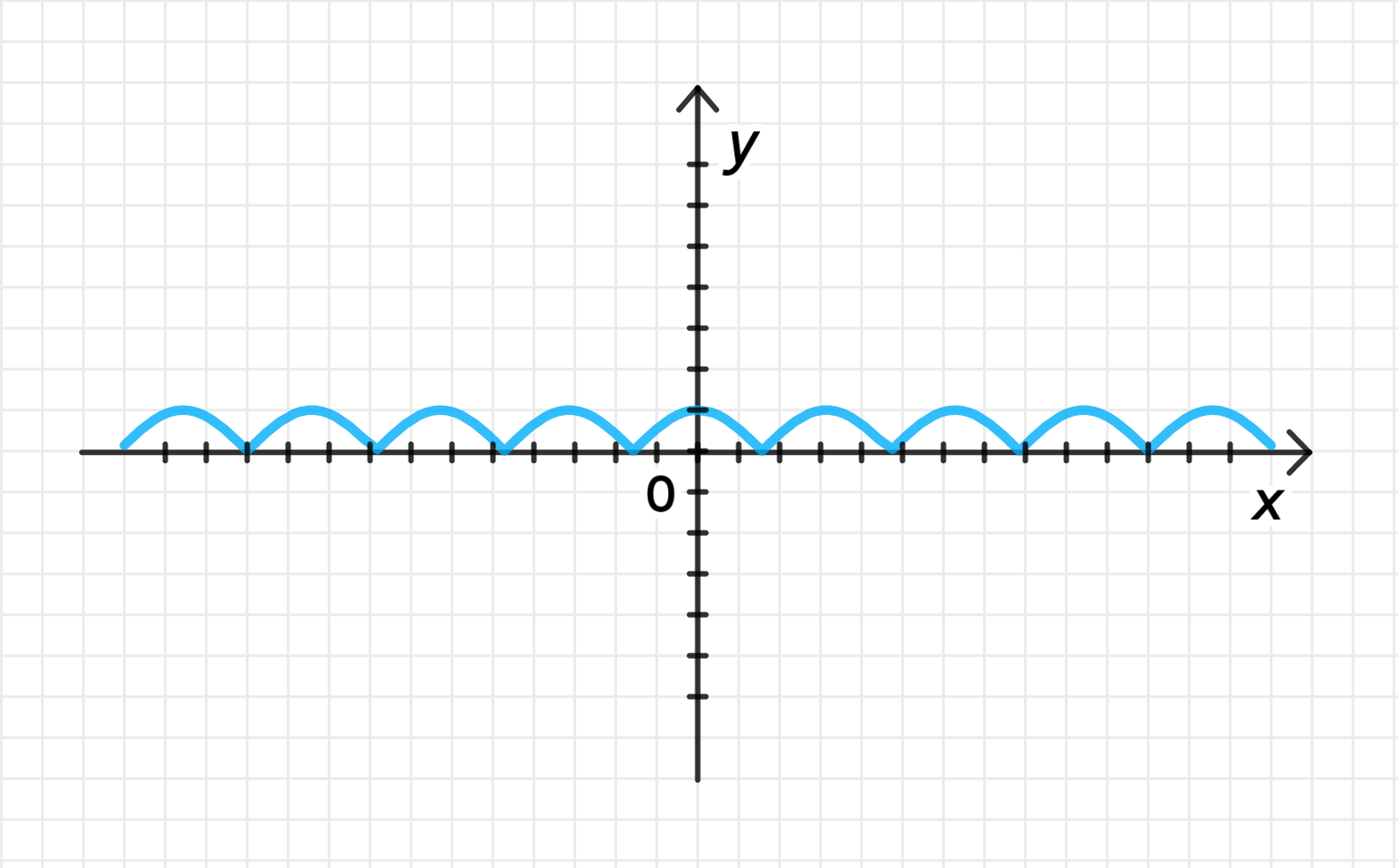
в) $y=\mathrm{\mid }\cos x\mathrm{\mid }$;

Построим график функции $y=\cos x$:

Как уже было рассмотрено, график функции $y=\cos x$ представляет собой волну, которая начинается с максимума в точке $x=0$ и осциллирует между 1 и -1 с периодом $2\pi$.

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

Для функции $y=\mathrm{\mid }\cos x\mathrm{\mid }$ все отрицательные значения функции $y=\cos x$ будут отразиться относительно оси $Ox$ и подняты вверх.

Это означает, что все участки графика, где $\cos x$ принимает отрицательные значения (например, на интервале $(\pi ,2\pi )$), будут отображаться выше оси $Ox$, и график будет полностью положительным.

Например:

• Если на интервале $(\pi ,2\pi )$ значение функции $y=\cos x$ отрицательно, то после применения абсолютного значения оно станет положительным.

Таким образом, график $y=\mathrm{\mid }\cos x\mathrm{\mid }$ будет выглядеть как волна, где все отрицательные части будут заменены на положительные.

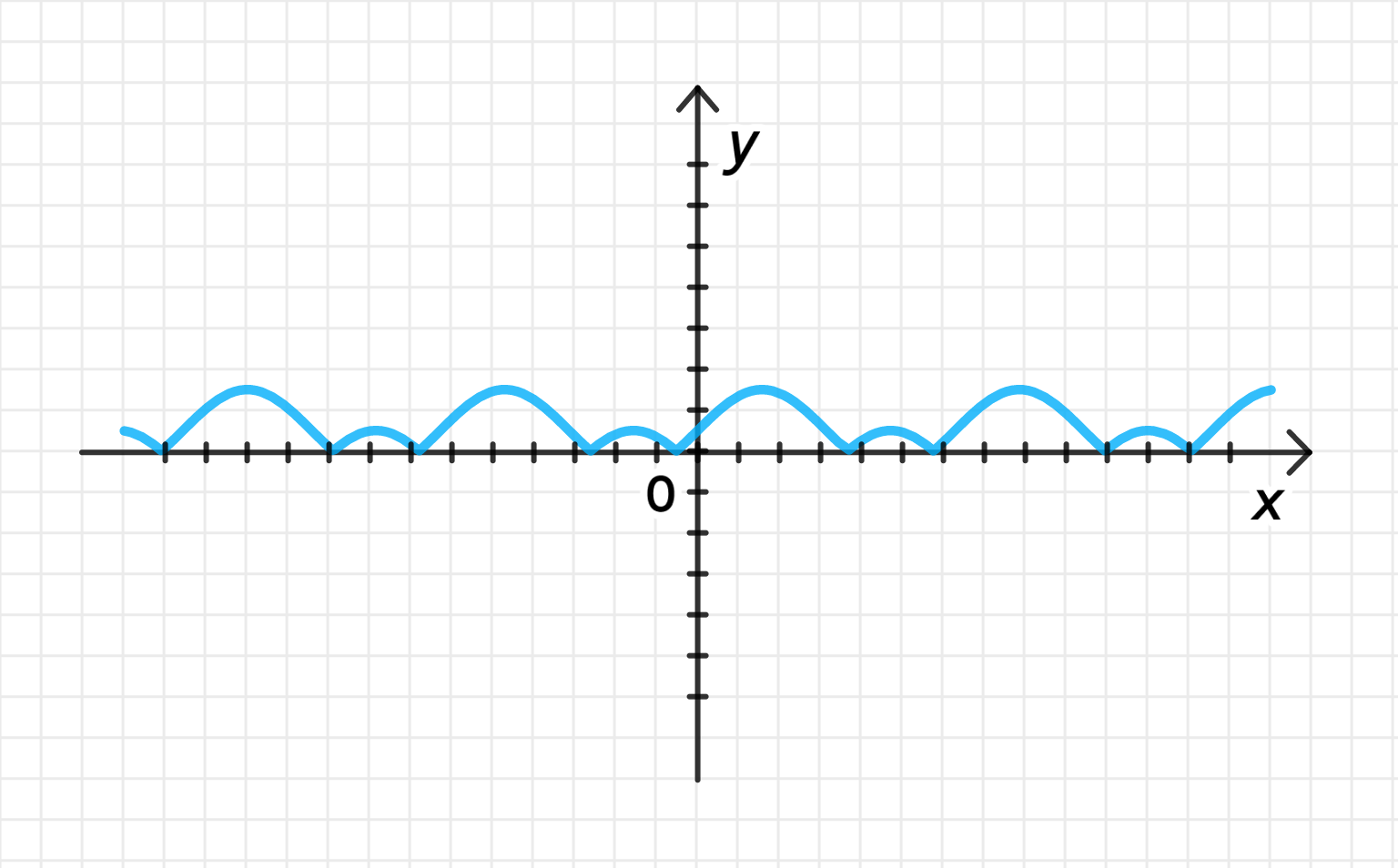
г) $y=\mid \sin x+\frac{1}{2}\mid$;

Построим график функции $y=\sin x$:

График функции $y=\sin x$ был описан ранее. Это волнообразная функция с периодом $2\pi$, колеблющаяся между -1 и 1, которая начинается с нуля в точке $x=0$.

Переместим его на $\frac{1}{2}$ единицы вверх вдоль оси ординат:

Для того чтобы переместить график на $\frac{1}{2}$ единицы вверх, нужно прибавить $\frac{1}{2}$ к каждому значению функции:

• Когда $x=0$, $\sin 0+\frac{1}{2}=0+\frac{1}{2}=\frac{1}{2}$.
• Когда $x=\frac{\pi }{2}$, $\sin \frac{\pi }{2}+\frac{1}{2}=1+\frac{1}{2}=\frac{3}{2}$.
• Когда $x=\pi$, $\sin \pi +\frac{1}{2}=0+\frac{1}{2}=\frac{1}{2}$.
• Когда $x=\frac{3\pi }{2}$, $\sin \frac{3\pi }{2}+\frac{1}{2}=-1+\frac{1}{2}=-\frac{1}{2}$.
• Когда $x=2\pi$, $\sin 2\pi +\frac{1}{2}=0+\frac{1}{2}=\frac{1}{2}$.

Этот сдвиг вверх позволяет сместить график в положительную часть координатной оси $y$.

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

После того как график был сдвинут вверх, теперь нужно взять абсолютное значение. Все значения, которые оказались ниже оси $Ox$, будут отражены в верхнюю часть графика.

Например:

• Если на интервале $(\frac{3\pi }{2},2\pi )$ значение функции $\sin x+\frac{1}{2}$ оказалось отрицательным (например, $-\frac{1}{2}$), то оно будет отражено в положительную часть графика.

Таким образом, график функции $y=\mid \sin x+\frac{1}{2}\mid$ будет полностью положительным, и все колебания будут выше оси $Ox$.