ГДЗ по Алгебре 10 Класс Номер 16.56 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \sin |x|$;

б) $y = \sin \left| x — \frac{\pi}{3} \right|$;

в) $y = \cos |x|$;

г) $y = \cos \left| x + \frac{2\pi}{3} \right|$

а) $y = \sin |x|$;

Построим график функции $y = \sin x$;

Уберем часть графика, лежащую слева от оси $Oy$;

Отразим относительно оси $Oy$ часть графика, лежащую справа:

б) $y = \sin \left| x — \frac{\pi}{3} \right|$;

Построим график функции $y = \sin x$;

Переместим его на $\frac{\pi}{3}$ единицы вправо вдоль оси абсцисс;

Уберем часть графика, лежащую слева от прямой $x = \frac{\pi}{3}$;

Отразим относительно нее часть графика, лежащую справа:

в) $y = \cos |x|$;

Построим график функции $y = \cos x$;

Уберем часть графика, лежащую слева от оси $Oy$;

Отразим относительно оси $Oy$ часть графика, лежащую справа:

г) $y = \cos \left| x + \frac{2\pi}{3} \right|$;

Построим график функции $y = \cos x$;

Переместим его на $\frac{2\pi}{3}$ единицы влево вдоль оси абсцисс;

Уберем часть графика, лежащую слева от прямой $x = -\frac{2\pi}{3}$;

Отразим относительно нее часть графика, лежащую справа:

а) $y = \sin |x|$

Этапы построения графика:

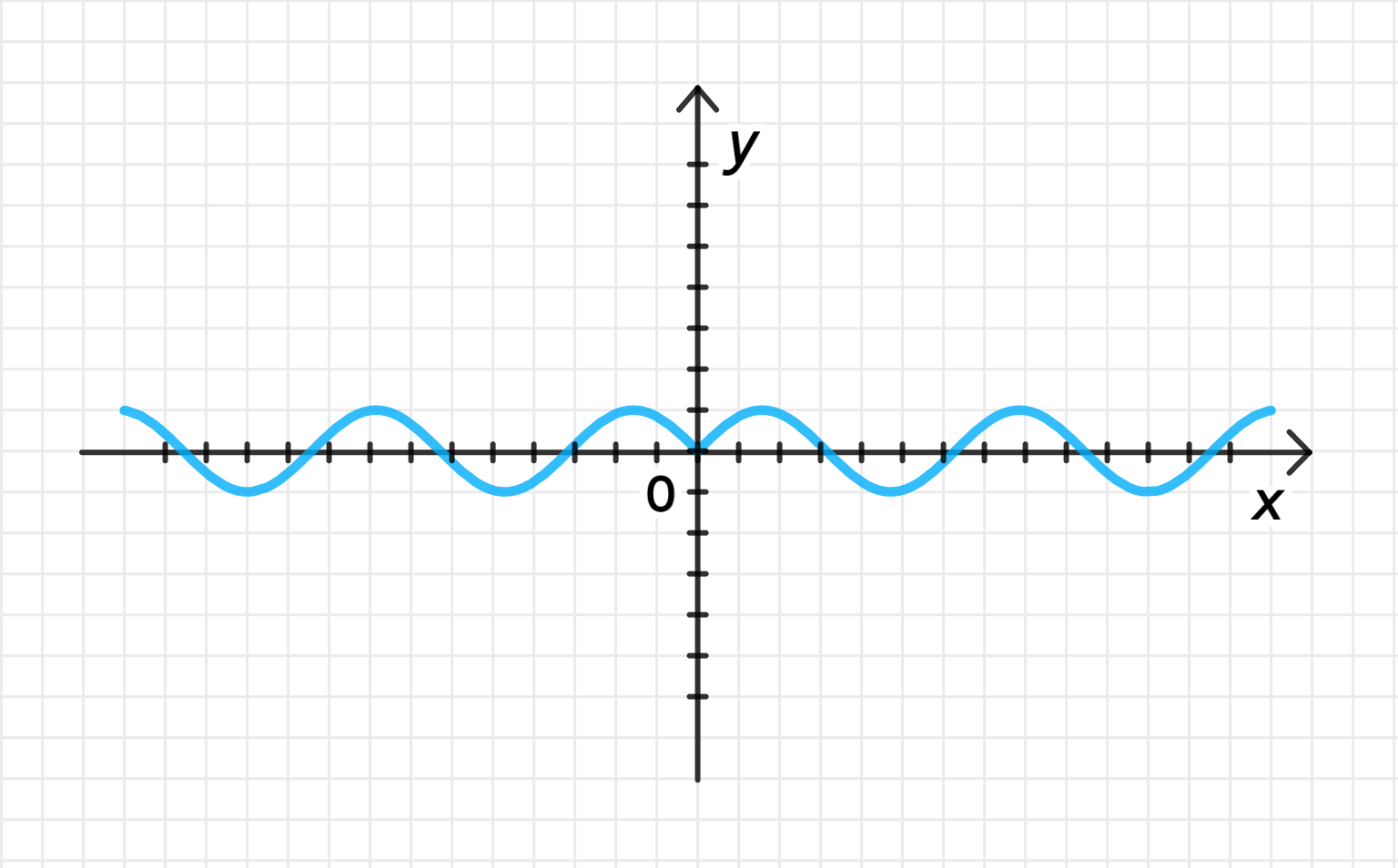
Построим график функции $y = \sin x$:

• График функции $y = \sin x$ является синусоидой, которая колеблется между значениями -1 и 1. Она периодична с периодом $2\pi$. График начинается в точке $(0, 0)$, затем достигает максимума $y = 1$ в точке $x = \frac{\pi}{2}$, минимума $y = -1$ в точке $x = \frac{3\pi}{2}$, и снова проходит через $y = 0$ в точке $x = 2\pi$.

Уберем часть графика, лежащую слева от оси $Oy$:

• Так как у нас абсолютная величина $|x|$, то график для $x < 0$ и $x > 0$ будет симметричным относительно оси $Oy$. Таким образом, часть графика, которая лежит слева от оси $Oy$, будет удалена.

Отразим график относительно оси $Oy$:

• График для $x > 0$ отразится относительно оси $Oy$, то есть его значение для положительных $x$ будет повторяться и для отрицательных $x$.

Таким образом, график $y = \sin |x|$ будет симметричен относительно оси $Oy$, и это будет синусоида, повторяющаяся как для $x > 0$, так и для $x < 0$.

б) $y = \sin \left| x — \frac{\pi}{3} \right|$

Этапы построения графика:

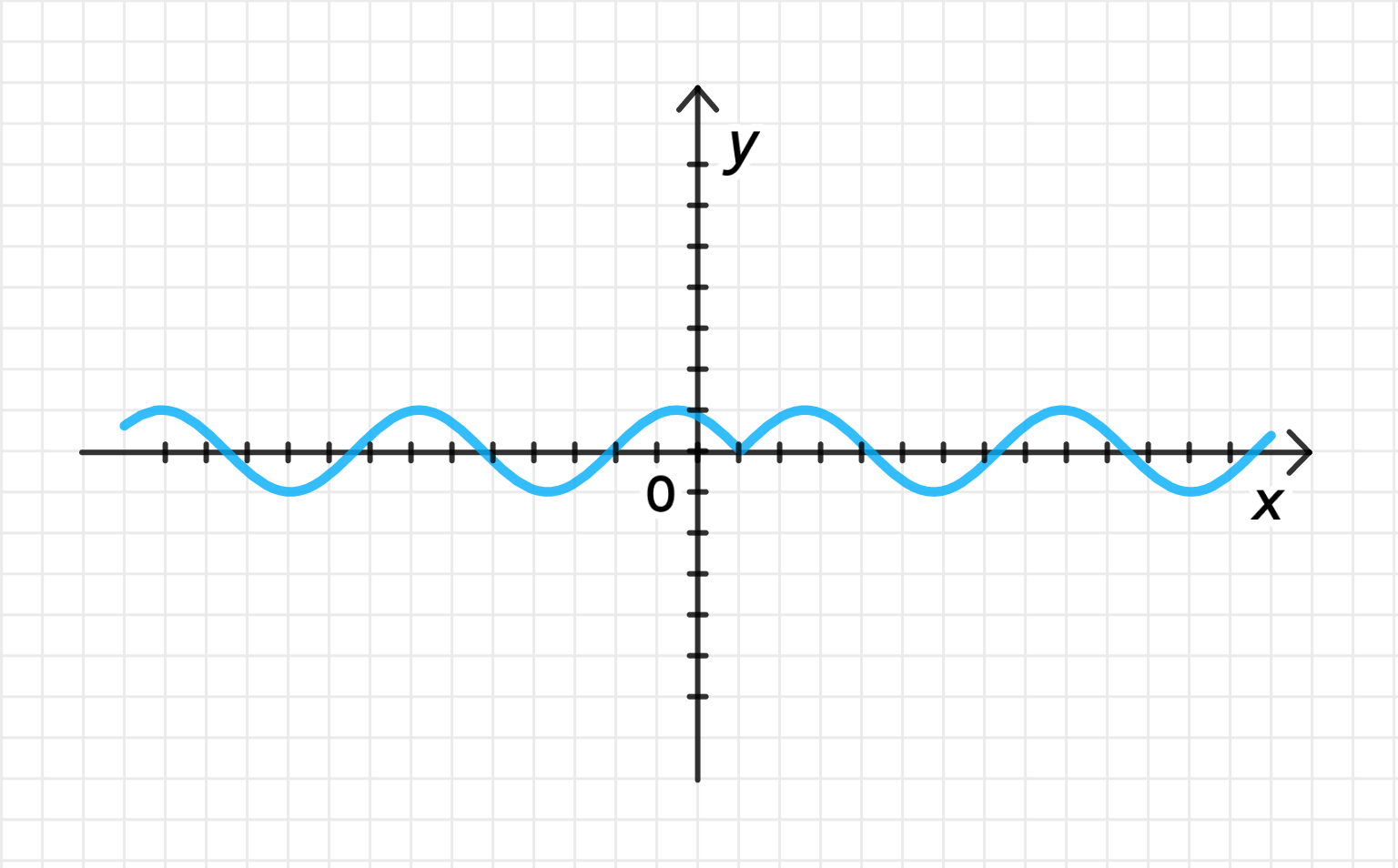
Построим график функции $y = \sin x$:

• Сначала строим обычную синусоиду $y = \sin x$, как и в предыдущем примере.

Переместим график на $\frac{\pi}{3}$ единицы вправо вдоль оси абсцисс:

• Операция $x — \frac{\pi}{3}$ означает сдвиг графика функции $\sin x$ на $\frac{\pi}{3}$ вправо. То есть, все точки графика сдвигаются вправо, и новый график будет начинаться в точке $\left( \frac{\pi}{3}, 0 \right)$.

Уберем часть графика, лежащую слева от прямой $x = \frac{\pi}{3}$:

• Поскольку у нас абсолютная величина $|x — \frac{\pi}{3}|$, мы убираем все, что находится слева от точки $x = \frac{\pi}{3}$.

Отразим график относительно прямой $x = \frac{\pi}{3}$:

• Теперь часть графика, расположенная справа от прямой $x = \frac{\pi}{3}$, будет отражена относительно этой прямой, и появится симметричный фрагмент графика слева от этой прямой.

в) $y = \cos |x|$

Этапы построения графика:

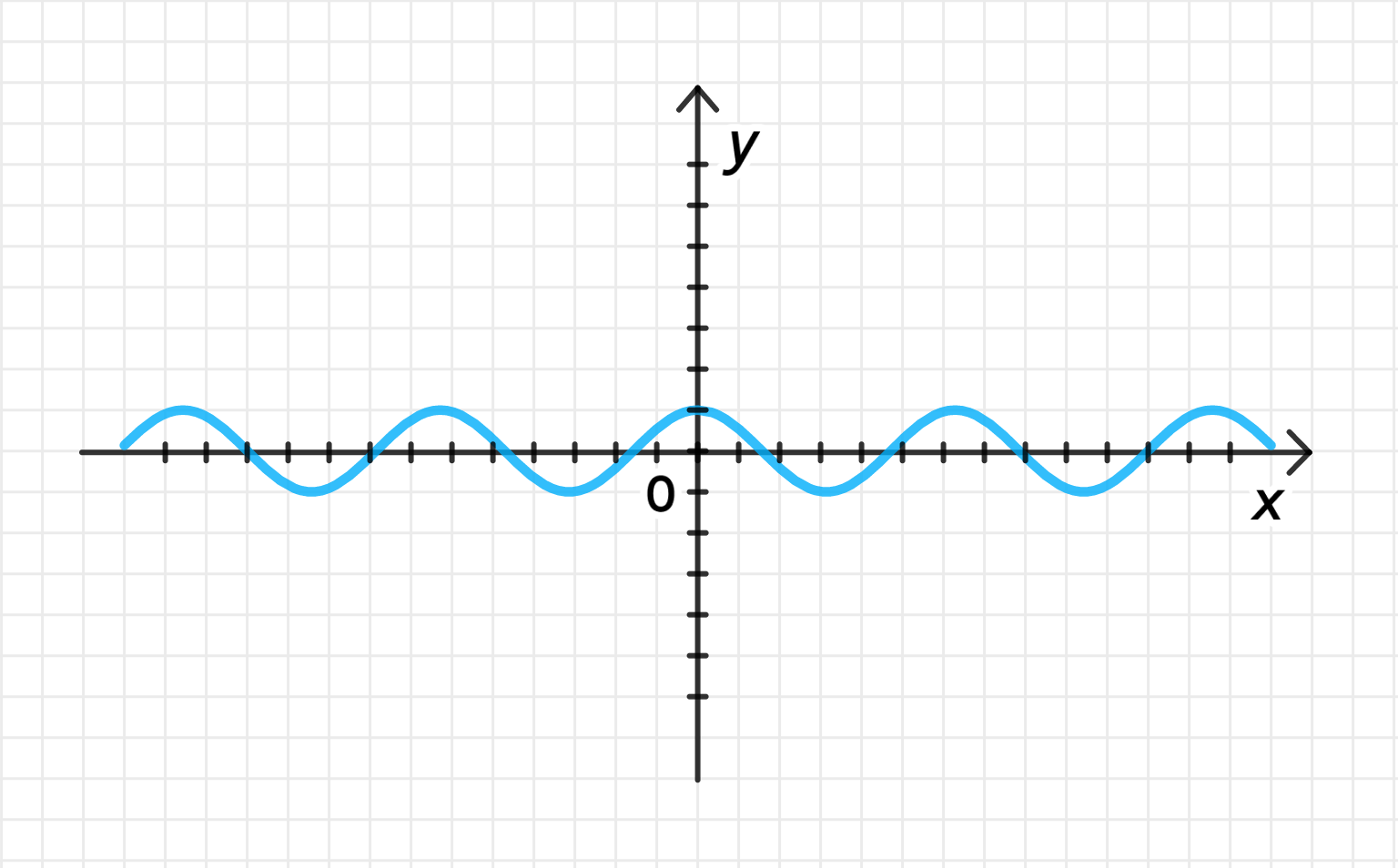
Построим график функции $y = \cos x$:

• График функции $y = \cos x$ является косинусоидой, которая также колеблется между значениями -1 и 1. Начинается она в точке $(0, 1)$, затем достигает минимального значения $y = -1$ в точке $x = \pi$, снова переходит через $y = 1$ в точке $x = 2\pi$.

Уберем часть графика, лежащую слева от оси $Oy$:

• Точно так же, как и в случае с синусом, для функции $y = \cos |x|$ мы убираем часть графика, расположенную слева от оси $Oy$.

Отразим график относительно оси $Oy$:

• График, расположенный справа от оси $Oy$, будет отзеркален относительно оси $Oy$.

Таким образом, график $y = \cos |x|$ будет симметричен относительно оси $Oy$, и повторяться как для $x > 0$, так и для $x < 0$.

г) $y = \cos \left| x + \frac{2\pi}{3} \right|$

Этапы построения графика:

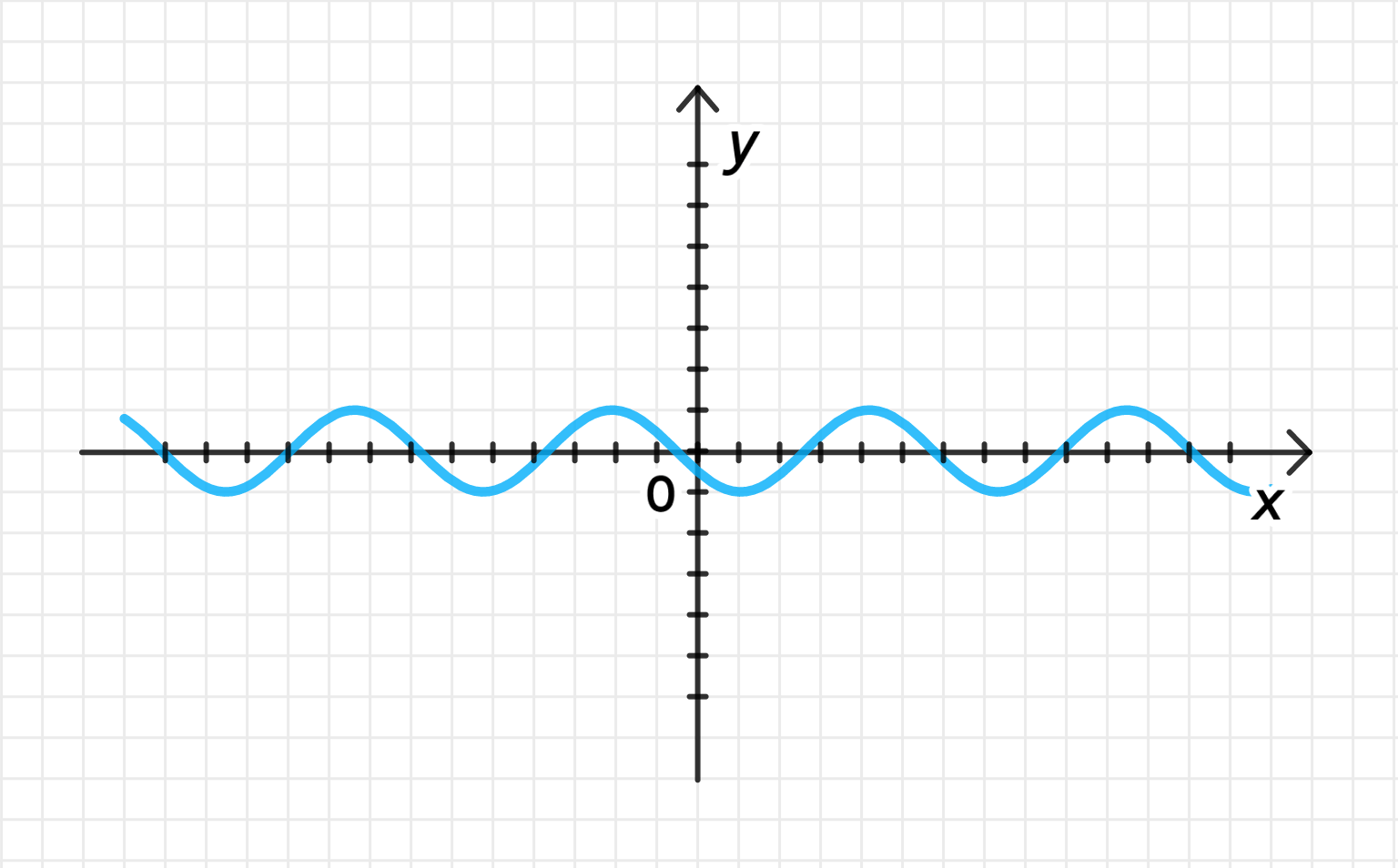
Построим график функции $y = \cos x$:

• Начинаем с построения стандартного графика косинуса, как и в предыдущем примере.

Переместим график на $\frac{2\pi}{3}$ единицы влево вдоль оси абсцисс:

• Операция $x + \frac{2\pi}{3}$ сдвигает график на $\frac{2\pi}{3}$ единицы влево. Это означает, что весь график будет сдвинут влево, и точка, где график пересекает ось $Oy$, будет смещена на $\frac{2\pi}{3}$.

Уберем часть графика, лежащую слева от прямой $x = -\frac{2\pi}{3}$:

• После сдвига графика, убираем все, что находится слева от прямой $x = -\frac{2\pi}{3}$.

Отразим график относительно прямой $x = -\frac{2\pi}{3}$:

• Отражаем часть графика, которая находится справа от прямой $x = -\frac{2\pi}{3}$, относительно этой прямой. Это создаст симметричный участок графика слева от этой прямой.