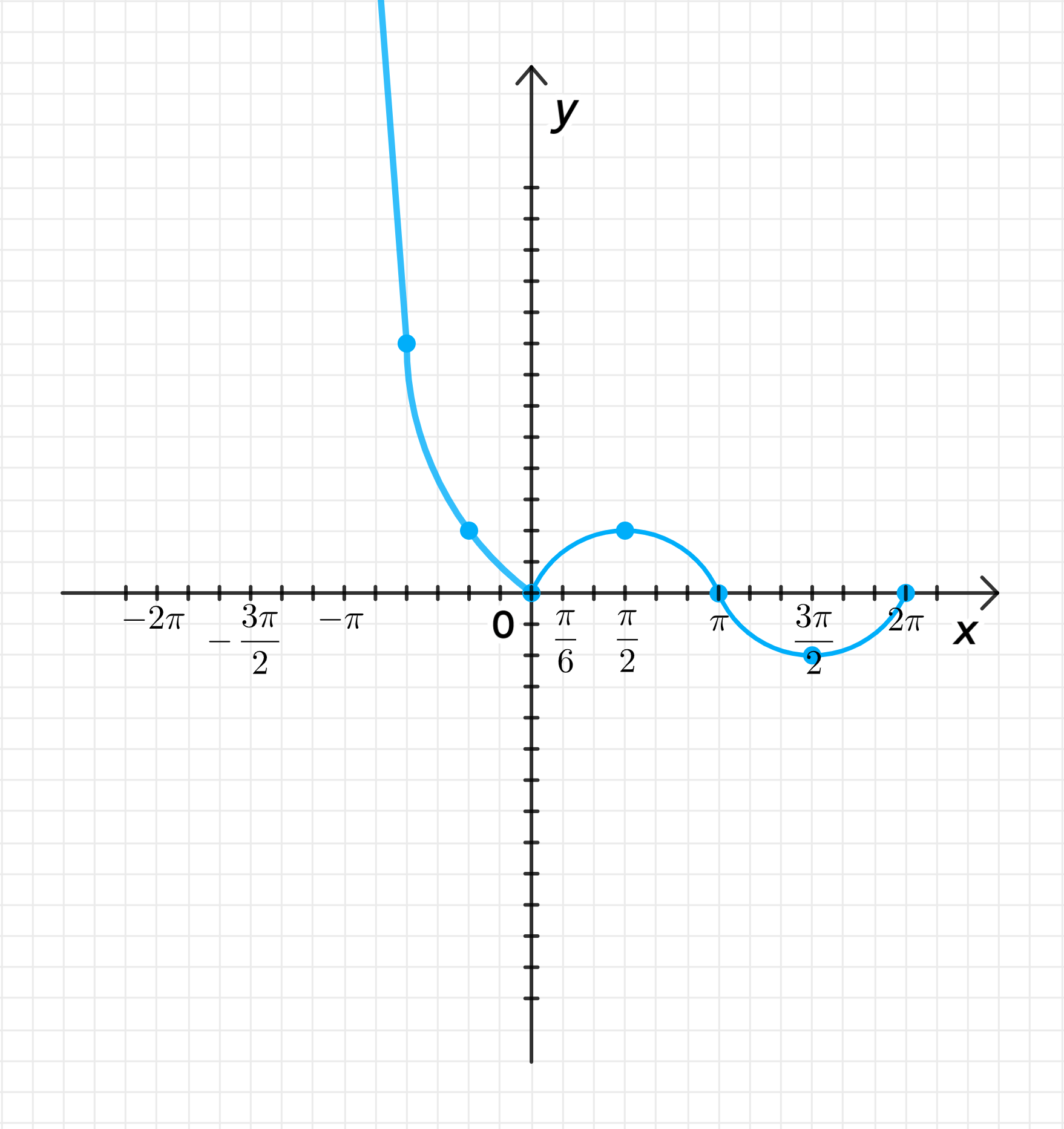ГДЗ по Алгебре 10 Класс Номер 16.57 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а) $y=\{\begin{array}{ll}{x}^2,& \text{если }x<0\\ \sin x,& \text{если }x\ge 0\end{array}$

б) $y=\{\begin{array}{ll}\sin x,& \text{если }x<0\\ x^2,& \text{если }x\ge 0\end{array}$

В данной задаче $n$ — целое неотрицательное число;

а) $y = \begin{cases} x^2, & \text{если } x < 0; \\ \sin x, & \text{если } x \geq 0; \end{cases}$

$y = \sin x$ — уравнение синусоиды:
$y(0) = \sin 0 = 0$;

$y = x^2$ — уравнение параболы:
$x_0 = 0, \quad y_0 = 0$;

Графики функции:

Свойства функции:

Область определения: $D(f) = (-\infty; +\infty)$;

Множество значений: $E(f) = [-1; +\infty)$;

Возрастает на $\left[ 0; \frac{\pi}{2} \right] \cup \left[ \frac{3\pi}{2} + 2\pi n; \frac{5\pi}{2} + 2\pi n \right]$;

Убывает на $(-\infty; 0] \cup \left[ \frac{\pi}{2} + 2\pi n; \frac{3\pi}{2} + 2\pi n \right]$;

$f(x) > 0$ на $(-\infty; 0) \cup (2\pi n; \pi + 2\pi n)$;

$f(x) < 0$ на $(\pi + 2\pi n; 2\pi + 2\pi n)$;

Функция ни четная, ни нечетная;

Функция не является периодической;

б) $y = \begin{cases} \sin x, & \text{если } x < 0; \\ x^2, & \text{если } x \geq 0; \end{cases}$

$y = \sin x$ — уравнение синусоиды:
$y(0) = \sin 0 = 0$;

$y = x^2$ — уравнение параболы:
$x_0 = 0, \quad y_0 = 0$;

Графики функции:

Свойства функции:

Область определения: $D(f) = (-\infty; +\infty)$;

Множество значений: $E(f) = [-1; +\infty)$;

Возрастает на $\left[ -\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n \right] \cup \left[ -\frac{\pi}{2}; +\infty \right)$;

Убывает на $\left[ -\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n \right]$;

$f(x) > 0$ на $(-2\pi — 2\pi n; -\pi — 2\pi n) \cup (0; +\infty)$;

$f(x) < 0$ на $(-\pi — 2\pi n; -2\pi n)$;

Функция ни четная, ни нечетная;

Функция не является периодической

а) Функция:

$$y = \begin{cases} x^2, & \text{если } x < 0; \\ \sin x, & \text{если } x \geq 0; \end{cases}$$

1) Уравнение синусоиды:

Для $x \geq 0$, функция $y = \sin x$ является синусоидой. Рассмотрим её значение в точке $x = 0$:

$$y(0) = \sin(0) = 0.$$

Это означает, что синусоида проходит через начало координат.

2) Уравнение параболы:

Для $x < 0$, функция $y = x^2$ представляет собой параболу, открывающуюся вверх. Рассмотрим значения функции для некоторых $x$:

• Для $x = -2$, $y = (-2)^2 = 4$.
• Для $x = -1$, $y = (-1)^2 = 1$.
• Для $x = 0$, $y = 0^2 = 0$.

Таким образом, значения функции для $x$ от -2 до 0 выглядят так:

3) График функции:

График состоит из двух частей:

• Для $x < 0$ график представляет собой часть параболы $y = x^2$.
• Для $x \geq 0$ график представляет собой синусоиду $y = \sin x$.

График будет выглядеть как сочетание параболы и синусоиды, где они соединяются в точке $(0, 0)$.

4) Свойства функции:

• Область определения: Функция определена для всех значений $x$, то есть $D(f) = (-\infty; +\infty)$.
• Множество значений: Поскольку синусоида $\sin x$ имеет значения от -1 до 1, а парабола $x^2$ принимает значения от 0 до $+\infty$, то общее множество значений функции будет $E(f) = [-1; +\infty)$.
• Возрастание: Функция возрастает на интервалах $\left[ 0; \frac{\pi}{2} \right]$ и $\left[ \frac{3\pi}{2} + 2\pi n; \frac{5\pi}{2} + 2\pi n \right]$, где $n$ — целое число. На этих интервалах функция синусоидальная и увеличивается.
• Убывание: Функция убывает на интервалах $(-\infty; 0]$ и $\left[ \frac{\pi}{2} + 2\pi n; \frac{3\pi}{2} + 2\pi n \right]$, где также учитывается поведение синусоиды.
• Положительные значения: Функция положительна на интервалах $(-\infty; 0)$ и $(2\pi n; \pi + 2\pi n)$.
• Отрицательные значения: Функция отрицательна на интервалах $(\pi + 2\pi n; 2\pi + 2\pi n)$.
• Четность: Функция ни четная, ни нечетная. Это видно, поскольку $y = x^2$ для $x < 0$ — четная функция, а $y = \sin x$ для $x \geq 0$ — нечетная функция, и комбинация этих двух функций не обладает симметрией относительно оси $y$.
• Периодичность: Функция не является периодической, так как синусоида имеет период, а парабола — нет.

б) Функция:

$$y = \begin{cases} \sin x, & \text{если } x < 0; \\ x^2, & \text{если } x \geq 0; \end{cases}$$

1) Уравнение синусоиды:

Для $x < 0$, функция $y = \sin x$ также является синусоидой. Рассмотрим её значение в точке $x = 0$:

$$y(0) = \sin(0) = 0.$$

Это означает, что синусоида также проходит через начало координат, но для этой функции синусоида будет наложена на область $x < 0$.

2) Уравнение параболы:

Для $x \geq 0$, функция $y = x^2$ представляет собой параболу, открывающуюся вверх. Рассмотрим значения функции для некоторых $x$:

• Для $x = 0$, $y = 0^2 = 0$.
• Для $x = 1$, $y = 1^2 = 1$.
• Для $x = 2$, $y = 2^2 = 4$.

Таким образом, значения функции для $x$ от 0 до 2 выглядят так:

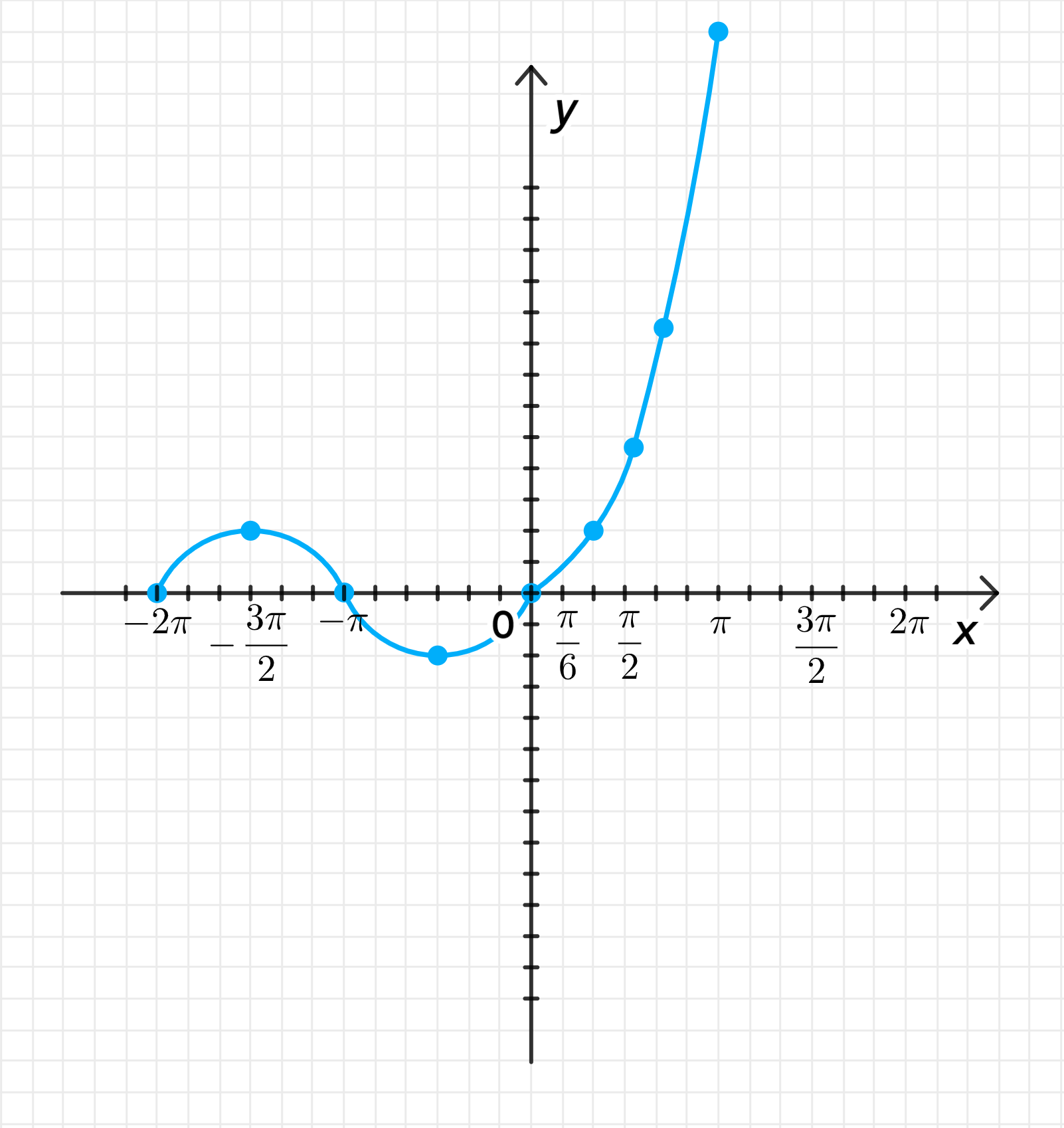
3) График функции:

График состоит из двух частей:

• Для $x < 0$ график будет синусоидой.
• Для $x \geq 0$ график будет параболой.

4) Свойства функции:

• Область определения: Функция определена для всех значений $x$, то есть $D(f) = (-\infty; +\infty)$.
• Множество значений: Поскольку синусоида $\sin x$ имеет значения от -1 до 1, а парабола $x^2$ принимает значения от 0 до $+\infty$, то общее множество значений функции будет $E(f) = [-1; +\infty)$.
• Возрастание: Функция возрастает на интервалах $\left[ -\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n \right]$ и $\left[ -\frac{\pi}{2}; +\infty \right)$, где $n$ — целое число.
• Убывание: Функция убывает на интервале $\left[ -\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n \right]$.
• Положительные значения: Функция положительна на интервалах $(-2\pi — 2\pi n; -\pi — 2\pi n) \cup (0; +\infty)$.
• Отрицательные значения: Функция отрицательна на интервале $(-\pi — 2\pi n; -2\pi n)$.
• Четность: Функция ни четная, ни нечетная.
• Периодичность: Функция не является периодической.