ГДЗ по Алгебре 10 Класс Номер 16.58 Профильный Уровень Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} \sin x, & \text{если } -\pi \leq x \leq 0, \\ \sqrt{x}, & \text{если } x > 0. \end{cases}$$

а) Вычислите: $f\left(-\frac{\pi}{2}\right)$, $f(0)$, $f(1)$, $f(\pi^2)$;

б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

Дана функция:

$$f(x) = \begin{cases} \sin x, & \text{если } -\pi \leq x \leq 0; \\ \sqrt{x}, & \text{если } x > 0 \end{cases}$$

а) Найдем значения:

$$f\left(-\frac{\pi}{2}\right) = \sin\left(-\frac{\pi}{2}\right) = -\sin\frac{\pi}{2} = -1;$$ $$f(0) = \sin 0 = 0;$$ $$f(1) = \sqrt{1} = 1;$$ $$f(\pi^2) = \sqrt{\pi^2} = \pi;$$

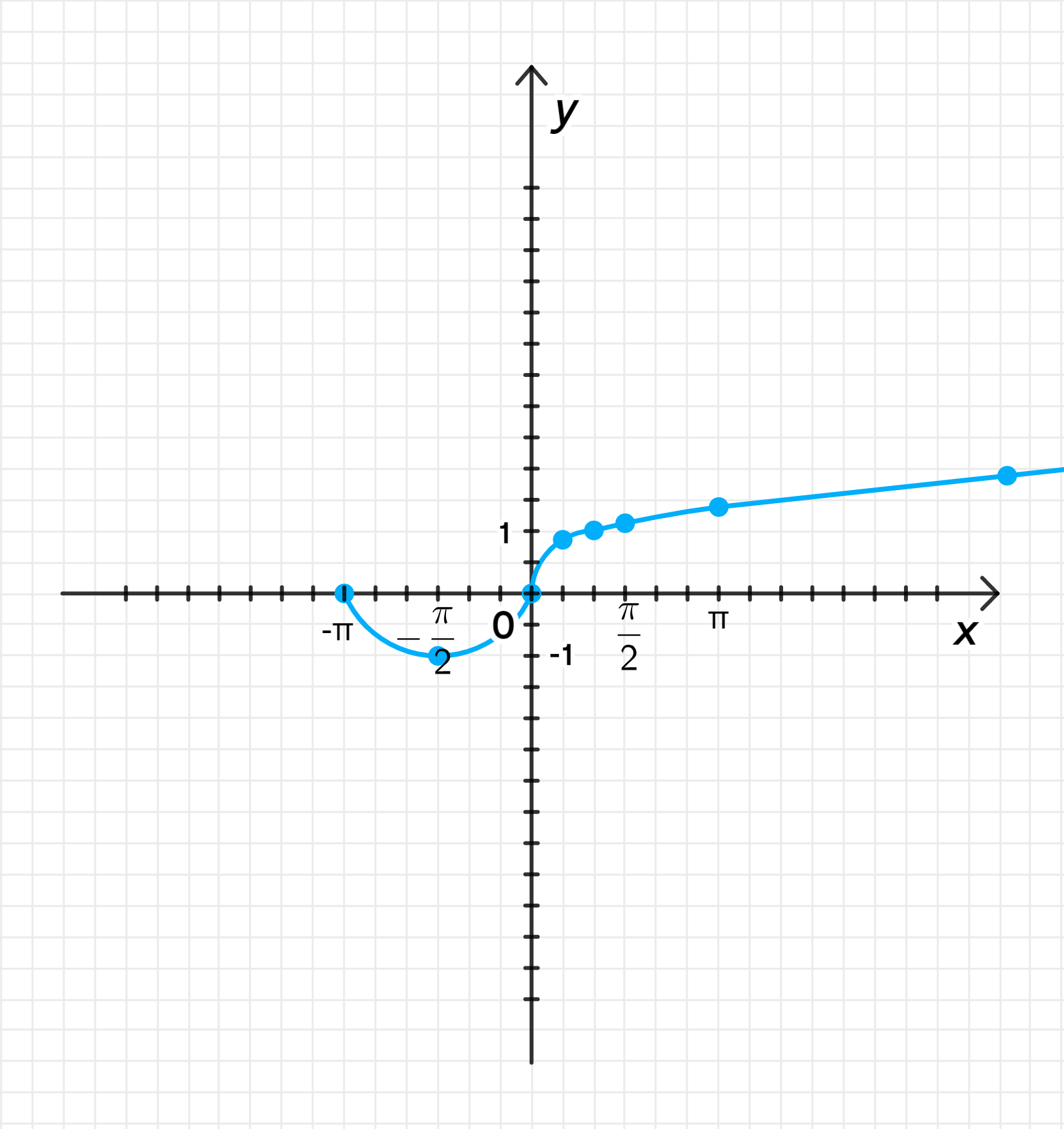
б) График функции:

$y = \sin x$ — уравнение синусоиды:

$$\begin{array}{|c|c|c|c|} \hline x & -\pi & -\frac{\pi}{2} & 0 \\ \hline y & 0 & -1 & 0 \\ \hline \end{array}$$

$y = \sqrt{x}$ — уравнение ветви параболы:
$x_0 = 0, \quad y_0 \geq 0;$

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

Графики функций:

в) Свойства функции:

• Область определения: $D(f) = [-\pi; +\infty);$
• Множество значений: $E(f) = [-1; +\infty);$
• Возрастает на $\left[-\frac{\pi}{2}; +\infty\right);$
• Убывает на $\left[-\pi; -\frac{\pi}{2}\right];$
• $f(x) \geq 0$ на $(0; +\infty);$
• $f(x) < 0$ на $(-\pi; 0);$
• Функция ни четная, ни нечетная;
• Функция не является периодической

Дана функция:

$$f(x) = \begin{cases} \sin x, & \text{если } -\pi \leq x \leq 0; \\ \sqrt{x}, & \text{если } x > 0 \end{cases}$$

Это определение функции в виде кусочной функции, которая имеет два разных выражения в зависимости от значения $x$. Рассмотрим каждую часть функции отдельно.

а) Найдем значения функции для нескольких точек.

1. $f\left(-\frac{\pi}{2}\right)$

Для нахождения значения функции в точке $x = -\frac{\pi}{2}$, нам нужно посмотреть, в какой части области определения лежит эта точка.

• Поскольку $-\pi \leq x \leq 0$, точка $x = -\frac{\pi}{2}$ попадает в область, где функция определяется как $f(x) = \sin x$.
• Следовательно, мы будем использовать выражение $f(x) = \sin x$.

Теперь вычислим:

$$f\left(-\frac{\pi}{2}\right) = \sin\left(-\frac{\pi}{2}\right)$$

Знаем, что:

$$\sin\left(-\frac{\pi}{2}\right) = -1$$

Следовательно, $f\left(-\frac{\pi}{2}\right) = -1$.

2. $f(0)$

Теперь находим значение функции в точке $x = 0$. Для этой точки:

• $0$ лежит в интервале $-\pi \leq x \leq 0$, поэтому снова используется выражение $f(x) = \sin x$.

Вычислим:

$$f(0) = \sin 0 = 0$$

3. $f(1)$

Теперь вычислим значение функции в точке $x = 1$. Здесь:

• $1 > 0$, поэтому используем выражение $f(x) = \sqrt{x}$.

Вычислим:

$$f(1) = \sqrt{1} = 1$$

4. $f(\pi^2)$

Для нахождения значения функции в точке $x = \pi^2$:

• $\pi^2 > 0$, значит, используем $f(x) = \sqrt{x}$.

Вычислим:

$$f(\pi^2) = \sqrt{\pi^2} = \pi$$

б) График функции.

1. График $y = \sin x$

График функции $y = \sin x$ представляет собой синусоиду. Нам нужно рассмотреть несколько значений $x$ в интервале $-\pi \leq x \leq 0$, чтобы построить график.

• $x = -\pi$: $y = \sin(-\pi) = 0$
• $x = -\frac{\pi}{2}$: $y = \sin\left(-\frac{\pi}{2}\right) = -1$
• $x = 0$: $y = \sin(0) = 0$

Запишем эти значения в таблице:

$$\begin{array}{|c|c|c|c|} \hline x & -\pi & -\frac{\pi}{2} & 0 \\ \hline y & 0 & -1 & 0 \\ \hline \end{array}$$

Таким образом, график функции $y = \sin x$ на интервале $-\pi \leq x \leq 0$ будет синусоидой, которая начинается и заканчивается в точке $0$, с минимумом в точке $x = -\frac{\pi}{2}$.

2. График $y = \sqrt{x}$

График функции $y = \sqrt{x}$ представляет собой часть параболы, начинающуюся в точке $(0, 0)$ и увеличивающуюся для положительных значений $x$. Мы рассмотрим несколько значений $x$ для построения графика на интервале $x > 0$:

• $x = 0$: $y = \sqrt{0} = 0$
• $x = 1$: $y = \sqrt{1} = 1$
• $x = 4$: $y = \sqrt{4} = 2$

Запишем эти значения в таблице:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

Таким образом, график функции $y = \sqrt{x}$ на интервале $x > 0$ представляет собой ветвь параболы, которая начинается в точке $(0, 0)$ и постепенно возрастает.

3. Суммарный график функции

График функции $f(x)$ будет состоять из двух частей:

• Для $-\pi \leq x \leq 0$ график будет соответствовать графику синусоиды.
• Для $x > 0$ график будет соответствовать графику параболы $y = \sqrt{x}$.

в) Свойства функции.

1. Область определения $D(f)$

Область определения функции — это множество значений $x$, для которых функция $f(x)$ определена. Рассмотрим каждый случай:

• Для $f(x) = \sin x$ область определения — это все значения $x$ от $-\pi$ до $0$, то есть $[-\pi, 0]$.
• Для $f(x) = \sqrt{x}$ область определения — это все значения $x \geq 0$, то есть $[0, +\infty)$.

Таким образом, общая область определения функции:

$$D(f) = [-\pi, +\infty)$$

2. Множество значений $E(f)$

Множество значений функции — это все возможные значения $f(x)$. Рассмотрим два случая:

• Для $f(x) = \sin x$ значения функции на интервале $-\pi \leq x \leq 0$ лежат в интервале $[-1, 0]$.
• Для $f(x) = \sqrt{x}$ значения функции на интервале $x \geq 0$ лежат в интервале $[0, +\infty)$.

Таким образом, объединяя эти два интервала, получаем множество значений функции:

$$E(f) = [-1, +\infty)$$

3. Возрастание и убывание

• На интервале $[-\pi, -\frac{\pi}{2}]$ функция убывает, потому что график $y = \sin x$ имеет убывающий участок.
• На интервале $[-\frac{\pi}{2}, 0]$ функция возрастает.
• На интервале $(0, +\infty)$ функция возрастает, так как $y = \sqrt{x}$ — возрастающая функция для $x > 0$.

4. Положительность функции

• Для $x > 0$, $f(x) = \sqrt{x}$, что всегда $f(x) \geq 0$.
• Для $-\pi \leq x < 0$, $f(x) = \sin x$, и здесь функция $f(x)$ может быть отрицательной.

Таким образом, функция:

• $f(x) \geq 0$ на $(0, +\infty)$
• $f(x) < 0$ на $[-\pi, 0)$

5. Четность и нечетность

Функция не является ни четной, ни нечетной:

• Для четности должно выполняться условие $f(-x) = f(x)$, что не выполняется для данной функции.
• Для нечетности должно выполняться условие $f(-x) = -f(x)$, что также не выполняется для данной функции.

6. Периодичность функции

Функция не является периодической, так как:

• Синусоиды на интервале $[-\pi, 0]$ имеют период, но парабола $y = \sqrt{x}$ на интервале $[0, +\infty)$ не повторяется.