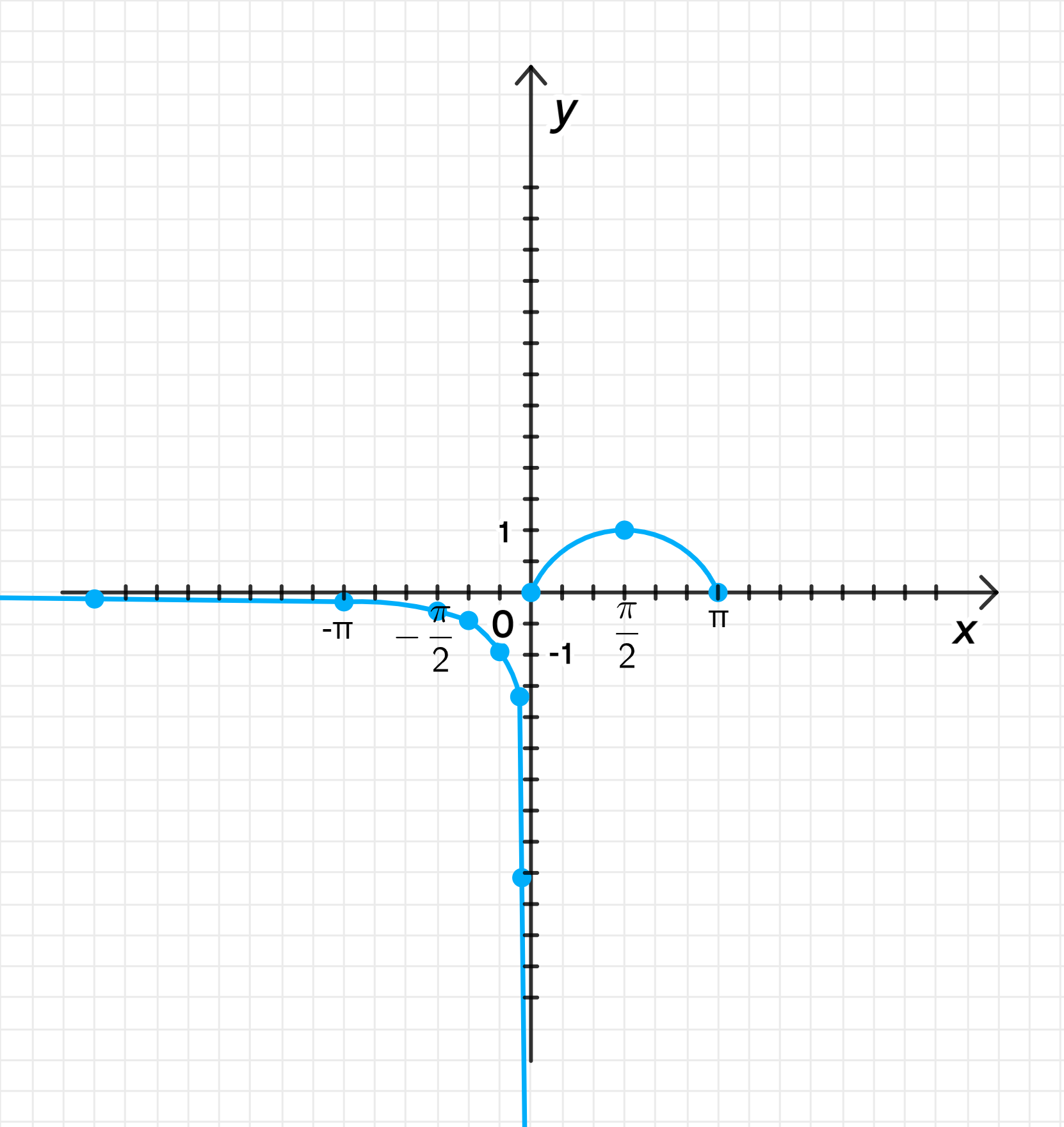ГДЗ по Алгебре 10 Класс Номер 16.59 Профильный Уровень Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} \frac{1}{x}, & \text{если } x < 0, \\ \sin x, & \text{если } 0 \leq x \leq \pi. \end{cases}$$

а) Вычислите: $f(-2)$, $f(0)$, $f(1)$;

б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

Дана функция:

$$f(x)=\{\begin{array}{ll}\frac{1}{x},& \text{если }x<0\\ \sin x,& \text{если }0\le x\le \pi \end{array};$$

а) Найдем значения:

$$f(-2)=\frac{1}{-2}=-0,5;$$$$f(0)=\sin 0=0;$$$$f(1)=\sin 1;$$

б) График функции:

$y=\sin x$ — уравнение синусоиды:

$$\begin{array}{cccc}x& 0& \frac{\pi }{2}& \pi \\ y& 0& 1& 0\end{array}$$

$y=\frac{1}{x}$ — уравнение гиперболы:

$$x_0=0,y_0\mathrm{\ne }0;$$$$\begin{array}{cccc}x& -2& -1& -0,5\\ y& -0,5& -1& -2\end{array}$$

Графики функций:

в) Свойства функции:

• Область определения: $D(f)=(-\mathrm{\infty };\pi ]$;
• Множество значений: $E(f)=(-\mathrm{\infty };1]$;
• Возрастает на $[0;\frac{\pi }{2}]$;
• Убывает на $(-\mathrm{\infty };0)\cup [\frac{\pi }{2};\pi ]$;
• $f(x)>0$ на $(0;\pi )$;
• $f(x)<0$ на $(-\mathrm{\infty };0)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической

Дана функция:

$$f(x)=\{\begin{array}{ll}\frac{1}{x},& \text{если }x<0\\ \sin x,& \text{если }0\le x\le \pi \end{array};$$

а) Найдем значения функции для определенных точек:

1. $f(-2)$

Мы ищем значение функции в точке $x=-2$.

• Поскольку $x=-2$ меньше нуля, то используем часть функции $f(x)=\frac{1}{x}$ (это определено для $x<0$).
• Подставим $x=-2$ в это выражение:

$$f(-2)=\frac{1}{-2}=-0,5$$

Ответ: $f(-2)=-0,5$.

2. $f(0)$

Теперь найдем значение функции в точке $x=0$.

• Поскольку $0\le x\le \pi$, то для $x=0$ используем часть функции $f(x)=\sin x$ (это определено для $0\le x\le \pi$).
• Подставим $x=0$ в это выражение:

$$f(0)=\sin (0)=0$$

Ответ: $f(0)=0$.

3. $f(1)$

Теперь найдем значение функции в точке $x=1$.

• Поскольку $0\le 1\le \pi$, то для $x=1$ используем часть функции $f(x)=\sin x$.
• Подставим $x=1$ в это выражение:

$$f(1)=\sin (1)$$

Так как значение $\sin (1)$ нельзя выразить в виде точного числа, его можно оставить в виде $\sin (1)$. Для приближенного значения это примерно равно 0.84147.

Ответ: $f(1)=\sin (1)\approx 0.84147$.

4. $f({\pi }^2)$

Теперь вычислим значение функции в точке $x={\pi }^2$.

• Поскольку ${\pi }^2>0$, то используем часть функции $f(x)=\sin x$, так как $0\le x\le \pi$, но ${\pi }^2$ больше $\pi$, и данное значение выходит за пределы области определения синуса.

Следовательно, функция не определена для $x={\pi }^2$ в данной области определения функции, так как предел области для синуса — это $\pi$.

Ответ: $f({\pi }^2)$ не существует, так как ${\pi }^2>\pi$, и функция $f(x)=\sin x$ не определена для $x>\pi$.

б) Построение графика функции $y=f(x)$:

1. График для $y=\sin x$

Функция $y=\sin x$ определена на интервале $0\le x\le \pi$. Нам нужно вычислить несколько ключевых значений для построения графика:

• $x=0$: $y=\sin (0)=0$
• $x=\frac{\pi }{2}$: $y=\sin \left(\frac{\pi }{2}\right)=1$
• $x=\pi$: $y=\sin (\pi )=0$

Запишем эти значения в таблице:

$$\begin{array}{cccc}x& 0& \frac{\pi }{2}& \pi \\ y& 0& 1& 0\end{array}$$

График функции $y=\sin x$ представляет собой синусоиду, которая начинается в точке $(0,0)$, достигает максимума в точке $(\frac{\pi }{2},1)$ и снова возвращается в точку $(\pi ,0)$.

2. График для $y=\frac{1}{x}$

Функция $y=\frac{1}{x}$ определена для $x<0$. На этом интервале функция является гиперболой с вертикальной асимптотой в точке $x=0$ (где функция стремится к бесконечности при приближении $x$ к нулю с левой стороны).

Рассмотрим несколько точек:

• $x=-2$: $y=\frac{1}{-2}=-0,5$
• $x=-1$: $y=\frac{1}{-1}=-1$
• $x=-0,5$: $y=\frac{1}{-0,5}=-2$

Запишем эти значения в таблице:

$$\begin{array}{cccc}x& -2& -1& -0,5\\ y& -0,5& -1& -2\end{array}$$

График функции $y=\frac{1}{x}$ будет гиперболой, направленной в левую нижнюю часть плоскости, с асимптотой $x=0$, где функция стремится к бесконечности.

3. Суммарный график

График функции $y=f(x)$ будет состоять из двух частей:

• Для $x<0$ график будет гиперболой, $y=\frac{1}{x}$.
• Для $0\le x\le \pi$ график будет синусоидой, $y=\sin x$.

в) Свойства функции $f(x)$:

1. Область определения $D(f)$

Область определения функции состоит из двух частей:

• Для $x<0$, функция определяется как $f(x)=\frac{1}{x}$.
• Для $0\le x\le \pi$, функция определяется как $f(x)=\sin x$.

Таким образом, область определения функции:

$$D(f)=(-\mathrm{\infty };\pi ]$$

2. Множество значений $E(f)$

Множество значений функции — это все возможные значения $f(x)$.

• Для $x<0$, функция $f(x)=\frac{1}{x}$ может принимать любые значения $y<0$, так как функция $\frac{1}{x}$ на $(-\mathrm{\infty },0)$ принимает все отрицательные значения.
• Для $0\le x\le \pi$, функция $f(x)=\sin x$ принимает значения в интервале от 0 до 1.

Объединяя эти два интервала, получаем множество значений:

$$E(f)=(-\mathrm{\infty };1]$$

3. Возрастает и убывает

• Функция $y=\sin x$ возрастает на интервале $[0;\frac{\pi }{2}]$.
• Функция $y=\frac{1}{x}$ убывает на интервале $(-\mathrm{\infty };0)$, и также убывает на интервале $[\frac{\pi }{2};\pi ]$, так как для $\sin x$ на этом интервале значения также убывают.

4. Положительность и отрицательность

• Для $x<0$, функция $f(x)=\frac{1}{x}$ всегда отрицательна, так как $x$ отрицательно.
• Для $0\le x\le \pi$, функция $f(x)=\sin x$ всегда положительна, так как значения синуса на этом интервале лежат в пределах от 0 до 1.

Ответ:

• $f(x)>0$ на $(0;\pi )$
• $f(x)<0$ на $(-\mathrm{\infty };0)$

5. Четность и нечетность

• Функция не является четной, так как для четности необходимо выполнение условия $f(-x)=f(x)$, что не выполняется для этой функции.
• Функция не является нечетной, так как для нечетности необходимо выполнение условия $f(-x)=-f(x)$, что также не выполняется для этой функции.

6. Периодичность

Функция не является периодической, так как:

• График синуса на интервале $[0;\pi ]$ не повторяется за пределами этого интервала.
• График функции $y=\frac{1}{x}$ также не имеет периодичности, так как он представляет собой гиперболу, а гипербола не повторяется.