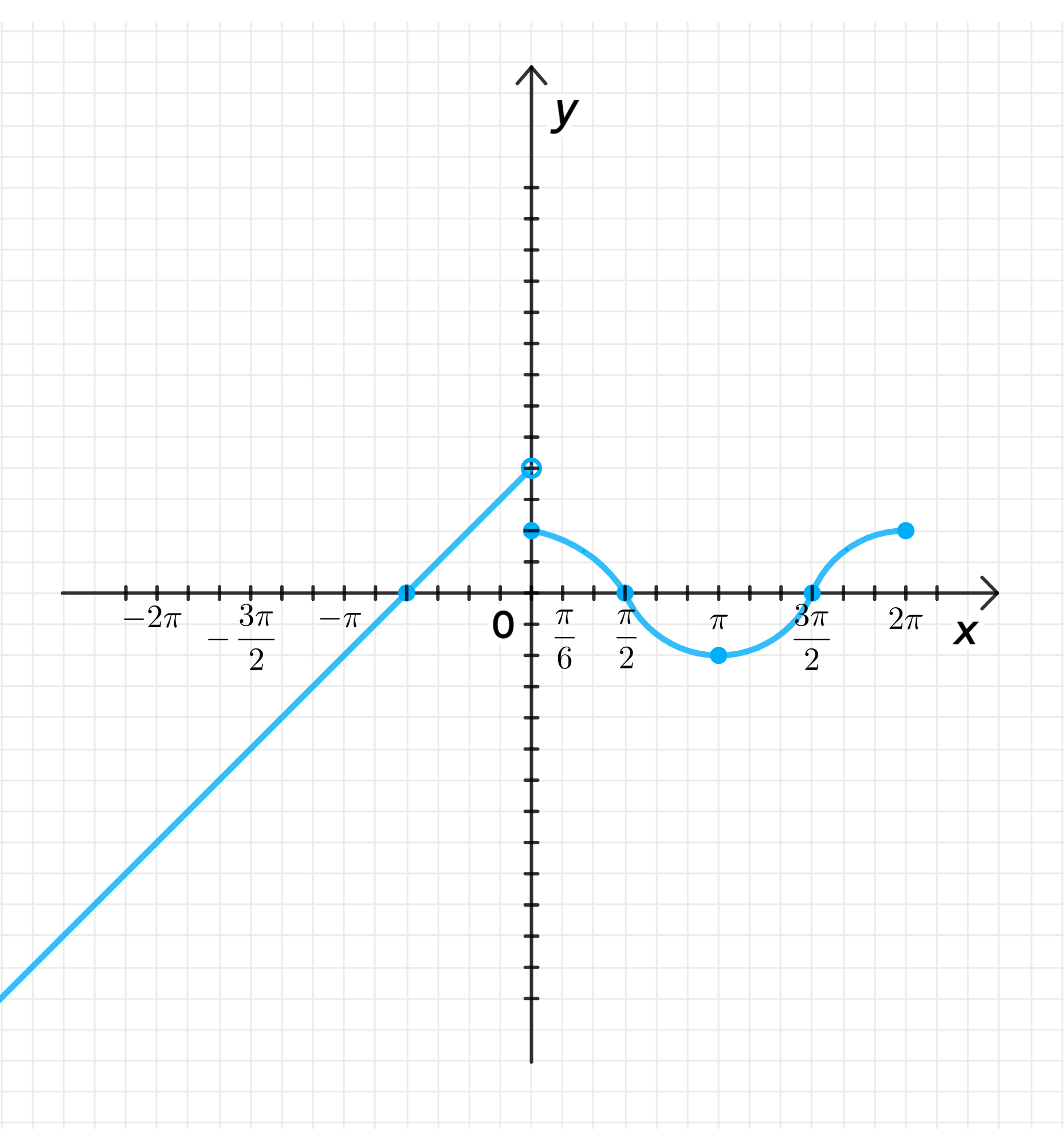ГДЗ по Алгебре 10 Класс Номер 16.60 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а) $y=\{\begin{array}{ll}x+2,& \text{если }x<0\\ \cos x,& \text{если }x\ge 0\end{array}$

б) $y=\{\begin{array}{ll}-\frac{2}{x},& \text{если }x<0\\ -\cos x,& \text{если }x\ge \end{array}$

В данной задаче

$n$ — целое неотрицательное число;

а) $y=\{\begin{array}{ll}x+2,& \text{если }x<0\\ \cos x,& \text{если }x\ge 0\end{array}$

$y=\cos x$ — уравнение синусоиды:
$y(0)=\cos 0=1$;

$y=x+2$ — уравнение прямой:

Графики функции:

Свойства функции:

• Область определения: $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$;
• Множество значений: $E(f)=(-\mathrm{\infty };2)$;
• Возрастает на $(-\mathrm{\infty };0)\cup [\pi +2\pi n;2\pi +2\pi n]$;
• Убывает на $[2\pi n;\pi +2\pi n]$;
• $f(x)>0$ на $(-2;\frac{\pi }{2})\cup (\frac{3\pi }{2}+2\pi n;\frac{5\pi }{2}+2\pi n)$;
• $f(x)<0$ на $(-\mathrm{\infty };-2)\cup (\frac{\pi }{2}+2\pi n;\frac{3\pi }{2}+2\pi n)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической;

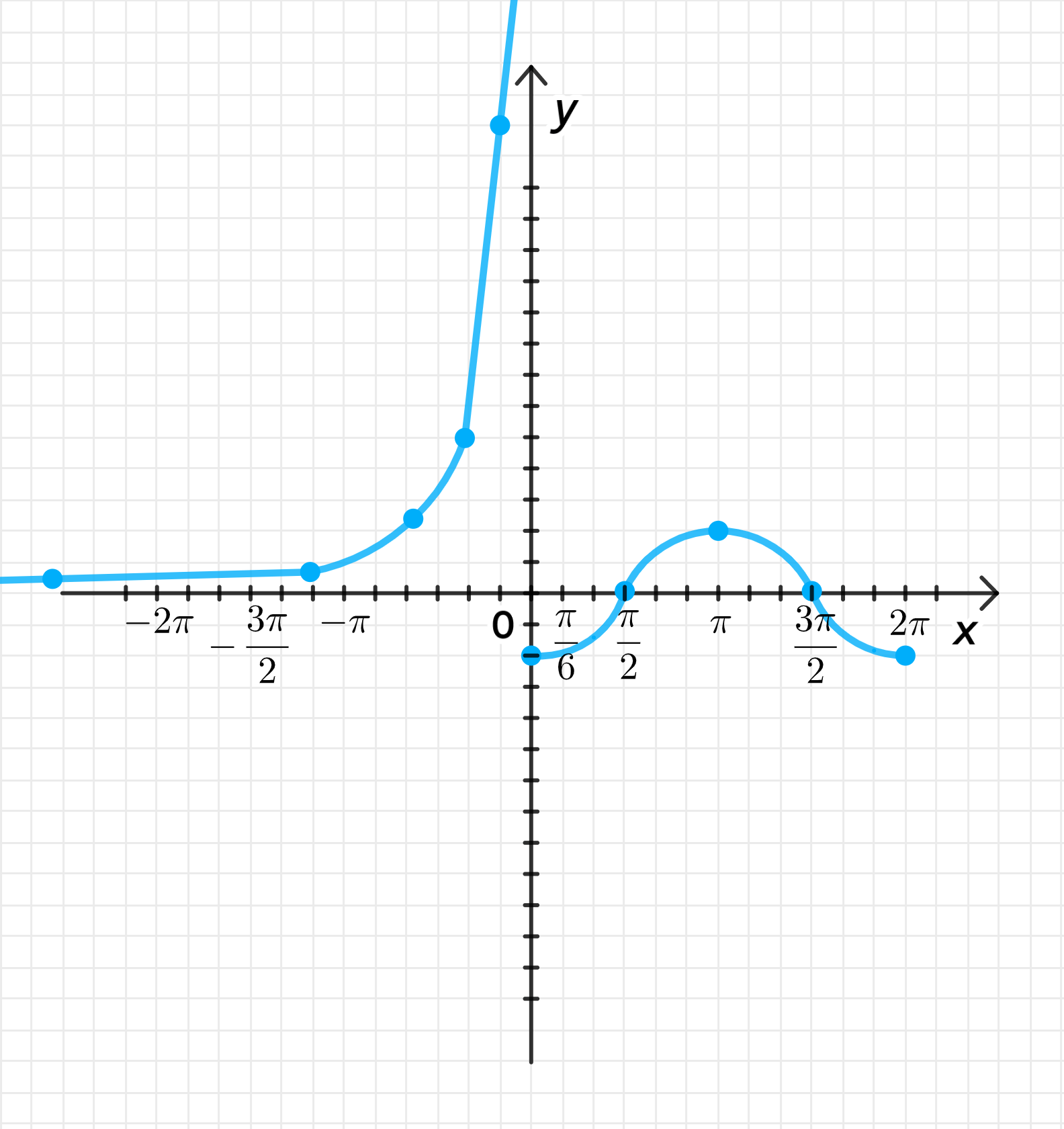
б) $y=\{\begin{array}{ll}-\frac{2}{x},& \text{если }x<0\\ -\cos x,& \text{если }x\ge 0\end{array}$

$y=-\cos x$ — уравнение синусоиды:
$y(0)=-\cos 0=-1$;

$y=-\frac{2}{x}$ — уравнение гиперболы:

Графики функции:

Свойства функции:

• Область определения: $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$;
• Множество значений: $E(f)=[-1;+\mathrm{\infty })$;
• Возрастает на $(-\mathrm{\infty };0)\cup [2\pi n;\pi +2\pi n]$;
• Убывает на $[\pi +2\pi n;2\pi +2\pi n]$;
• $f(x)>0$ на $(-\mathrm{\infty };0)\cup (\frac{\pi }{2}+2\pi n;\frac{3\pi }{2}+2\pi n)$;
• $f(x)<0$ на $(0;\frac{\pi }{2})\cup (\frac{3\pi }{2}+2\pi n;\frac{5\pi }{2}+2\pi n)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической

а) Функция:

$$y=\{\begin{array}{ll}x+2,& \text{если }x<0\\ \cos x,& \text{если }x\ge 0\end{array}$$

1) $y=\cos x$ — уравнение синусоиды

Для $x\ge 0$ функция $y=\cos x$ — это стандартная косинусоида. Известно, что:

• $y(0)=\cos (0)=1$ (точка на оси $y$ при $x=0$).

Также важно отметить, что косинусоида имеет период $2\pi$, то есть она повторяется через каждые $2\pi$ единиц по оси $x$.

2) $y=x+2$ — уравнение прямой

Для $x<0$ функция описана линейной прямой $y=x+2$. Чтобы понять, как она выглядит, можно подставить несколько значений для $x$:

• При $x=-2$: $y=-2+2=0$.
• При $x=2$: $y=2+2=4$.

Таким образом, эта прямая пересекает ось $y$ в точке $y=2$, а на оси $x$ — в точке $x=-2$.

3) Графики функции

4) Свойства функции

• Область определения $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$ — функция определена для всех значений $x$, так как она определена как для отрицательных, так и для неотрицательных значений $x$.
• Множество значений $E(f)=(-\mathrm{\infty };2)$:
  • Для части $y=x+2$, так как $x$ может быть любым отрицательным числом, то $y$ будет принимать значения от $2$ до $-\mathrm{\infty }$.
  • Для части $y=\cos x$ множество значений ограничено интервалом от $-1$ до $1$. На пересечении этих двух частей, для $x=0$, функция будет принимать значение $y=1$, что соответствует максимальному значению косинуса.
• Возрастает на $(-\mathrm{\infty };0)\cup [\pi +2\pi n;2\pi +2\pi n]$:
  • Прямая $y=x+2$ возрастает для всех $x<0$.
  • Косинусоида возрастает на интервалах $[\pi +2\pi n;2\pi +2\pi n]$, где $n$ — целое число.
• Убывает на $[2\pi n;\pi +2\pi n]$:
  • Косинусоида убывает на этих интервалах.
• $f(x)>0$ на $(-2;\frac{\pi }{2})\cup (\frac{3\pi }{2}+2\pi n;\frac{5\pi }{2}+2\pi n)$:
  • Для $x<0$, $f(x)>0$ на интервале $(-2;0)$.
  • Для $x\ge 0$, косинусоида положительна на интервалах, например, между $0$ и $\frac{\pi }{2}$, а также на других подобных интервалах.
• $f(x)<0$ на $(-\mathrm{\infty };-2)\cup (\frac{\pi }{2}+2\pi n;\frac{3\pi }{2}+2\pi n)$:
  • Функция $f(x)$ будет отрицательной для $x<-2$ и на интервалах косинусоиды, например, от $\frac{\pi }{2}$ до $\frac{3\pi }{2}$, и на подобных интервалах.
• Функция ни четная, ни нечетная:
  • Эта функция не является ни четной, ни нечетной, так как $f(x)\mathrm{\ne }f(-x)$ и $f(x)\mathrm{\ne }-f(x)$.
• Функция не является периодической:
  • Она не является периодической, так как линейная часть функции не повторяется, в отличие от косинусоидальной.

б) Функция:

$$y=\{\begin{array}{ll}-\frac{2}{x},& \text{если }x<0\\ -\cos x,& \text{если }x\ge 0\end{array}$$

1) $y=-\cos x$ — уравнение синусоиды

Для $x\ge 0$ функция $y=-\cos x$ — это косинусоида, но с измененным знаком. То есть, она будет начинаться от $y=-1$ в точке $x=0$ и будет колебаться между -1 и 1.

• $y(0)=-\cos (0)=-1$.

2) $y=-\frac{2}{x}$ — уравнение гиперболы

Для $x<0$ функция $y=-\frac{2}{x}$ — это гипербола, которая при приближении $x$ к нулю стремится к бесконечности (или минус бесконечности), а при удалении от нуля $y$ стремится к нулю. Подставим несколько значений:

• При $x=-2$: $y=-\frac{2}{-2}=1$.
• При $x=-1$: $y=-\frac{2}{-1}=2$.
• При $x=-0.5$: $y=-\frac{2}{-0.5}=4$.

3) Графики функции

4) Свойства функции

• Область определения $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$, так как функция определена как для $x<0$, так и для $x\ge 0$.
• Множество значений $E(f)=[-1;+\mathrm{\infty })$:
  • Для части $y=-\frac{2}{x}$, так как $x$ принимает значения меньше нуля, то $y$ будет больше нуля и стремится к бесконечности.
  • Для части $y=-\cos x$, значения $y$ будут от -1 до 0, что полностью покрывает множество значений.
• Возрастает на $(-\mathrm{\infty };0)\cup [2\pi n;\pi +2\pi n]$:
  • Гипербола возрастает для $x<0$ и на соответствующих интервалах для косинусоиды.
• Убывает на $[\pi +2\pi n;2\pi +2\pi n]$:
  • Гипербола убывает при удалении от нуля и на интервалах косинусоиды.
• $f(x)>0$ на $(-\mathrm{\infty };0)\cup (\frac{\pi }{2}+2\pi n;\frac{3\pi }{2}+2\pi n)$:
  • Гипербола положительна для всех отрицательных значений $x$ и на интервалах косинусоиды, где $\cos x$ отрицателен.
• $f(x)<0$ на $(0;\frac{\pi }{2})\cup (\frac{3\pi }{2}+2\pi n;\frac{5\pi }{2}+2\pi n)$:
  • Косинусоида отрицательна на интервалах, где $\cos x$ положителен.
• Функция ни четная, ни нечетная:
  • Функция не является четной или нечетной.
• Функция не является периодической:
  • Эта функция также не является периодической.