ГДЗ по Алгебре 10 Класс Номер 16.64 Профильный Уровень Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} 2x + 2\pi, & \text{если } x \leq -\pi, \\ \sin x, & \text{если } -\pi < x \leq 0, \\ -2x, & \text{если } x > 0. \end{cases}$$

а) Вычислите: $f(-\pi — 2)$, $f\left(-\frac{\pi}{6}\right)$, $f(2)$;

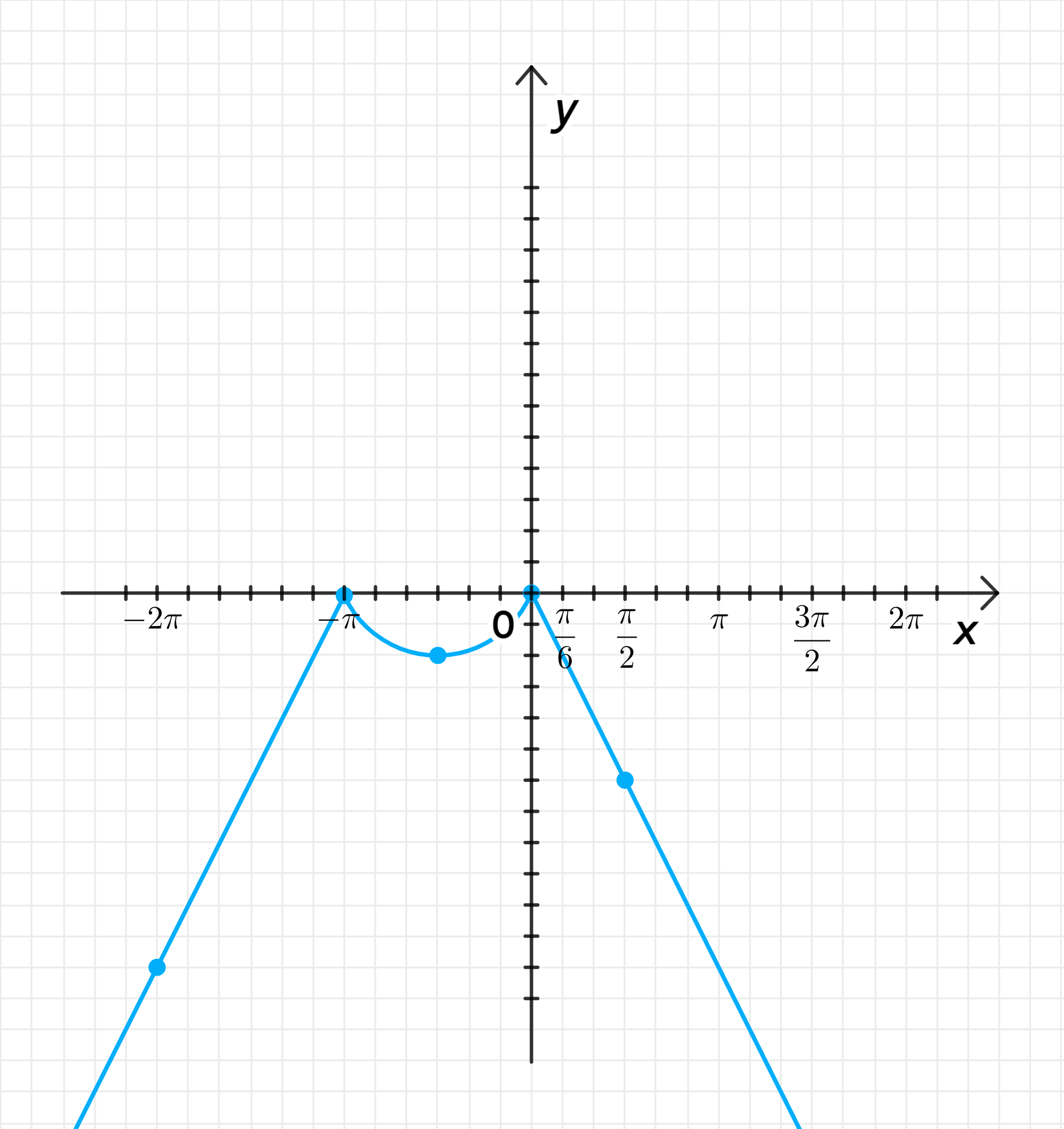
б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

Дана функция:

$$f(x) = \begin{cases} 2x + 2\pi, & \text{если } x \leq -\pi \\ \sin x, & \text{если } -\pi < x \leq 0 \\ -2x, & \text{если } x > 0 \end{cases}$$

а) Найдем значения:

$$f(-\pi — 2) = 2(-\pi — 2) + 2\pi = -2\pi — 4 + 2\pi = -4;$$ $$f\left(-\frac{\pi}{6}\right) = \sin\left(-\frac{\pi}{6}\right) = -\sin\frac{\pi}{6} = -0.5;$$ $$f(2) = -2 \cdot 2 = -4;$$

б) График функции:

$y = 2x + 2\pi$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & -\frac{4\pi}{3} & -\pi \\ \hline y & \approx -2 & 0 \\ \hline \end{array}$$

$y = \sin x$ — уравнение синусоиды:

$$\begin{array}{|c|c|c|c|} \hline x & -\pi & -\frac{\pi}{2} & 0 \\ \hline y & 0 & -1 & 0 \\ \hline \end{array}$$

$y = -2x$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 0 & -2 \\ \hline \end{array}$$

Графики функций:

в) Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = (-\infty; 0]$;
• Возрастает на $(-\infty; -\pi] \cup \left[-\frac{\pi}{2}; 0\right]$;
• Убывает на $\left[-\pi; -\frac{\pi}{2}\right] \cup [0; +\infty)$;
• $f(x) < 0$ на $(-\infty; -\pi) \cup (-\pi; 0) \cup (0; +\infty)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической.

Дана функция:

$$f(x) = \begin{cases} 2x + 2\pi, & \text{если } x \leq -\pi \\ \sin x, & \text{если } -\pi < x \leq 0 \\ -2x, & \text{если } x > 0 \end{cases}$$

Функция задана кусочно и представляет собой три разные части, определенные на разных интервалах:

1. Линейная функция $y = 2x + 2\pi$ на интервале $x \leq -\pi$.
2. Тригонометрическая функция $y = \sin x$ на интервале $-\pi < x \leq 0$.
3. Линейная функция $y = -2x$ на интервале $x > 0$.

а) Найдем значения функции для заданных $x$:

1. $f(-\pi — 2)$:
   $x = -\pi — 2$ попадает в область, где $x \leq -\pi$, поэтому нужно использовать первое выражение для функции $f(x) = 2x + 2\pi$.

   $$f(-\pi — 2) = 2(-\pi — 2) + 2\pi = 2(-\pi) — 4 + 2\pi = -2\pi — 4 + 2\pi$$

   Упрощаем:

   $$f(-\pi — 2) = -4$$

   Таким образом, $f(-\pi — 2) = -4$.

2. $f\left( -\frac{\pi}{6} \right)$:
   $x = -\frac{\pi}{6}$ попадает в область $-\pi < x \leq 0$, где используется функция $f(x) = \sin x$. Поэтому нужно найти значение синуса для $x = -\frac{\pi}{6}$:

   $$f\left( -\frac{\pi}{6} \right) = \sin\left( -\frac{\pi}{6} \right)$$

   Мы знаем, что:

   $$\sin\left( -\frac{\pi}{6} \right) = -\sin\frac{\pi}{6} = -\frac{1}{2}$$

   Таким образом, $f\left( -\frac{\pi}{6} \right) = -0.5$.

3. $f(2)$:
   $x = 2$ попадает в область, где $x > 0$, и используется функция $f(x) = -2x$. Подставляем $x = 2$:

   $$f(2) = -2 \cdot 2 = -4$$

   Таким образом, $f(2) = -4$.

б) График функции:

$y = 2x + 2\pi$ — уравнение прямой:

Это линейная функция на интервале $x \leq -\pi$. Для того чтобы построить график, подставим два значения для $x$:

• При $x = -\frac{4\pi}{3}$:

  $$y = 2\left(-\frac{4\pi}{3}\right) + 2\pi = -\frac{8\pi}{3} + 2\pi = -\frac{8\pi}{3} + \frac{6\pi}{3} = -\frac{2\pi}{3}$$

• При $x = -\pi$:

  $$y = 2(-\pi) + 2\pi = -2\pi + 2\pi = 0$$

Таким образом, на интервале $x \leq -\pi$ функция $f(x) = 2x + 2\pi$ будет линейной, начиная от точки $(-\frac{4\pi}{3}, -\frac{2\pi}{3})$ и заканчивая в точке $(-\pi, 0)$.

$y = \sin x$ — уравнение синусоиды:

Это уравнение синуса на интервале $-\pi < x \leq 0$. Рассмотрим важные точки:

• При $x = -\pi$:

  $$y = \sin(-\pi) = 0$$

• При $x = -\frac{\pi}{2}$:

  $$y = \sin\left(-\frac{\pi}{2}\right) = -1$$

• При $x = 0$:

  $$y = \sin(0) = 0$$

Таким образом, график функции будет колебаться между 0 и -1 на интервале $-\pi < x \leq 0$.

$y = -2x$ — уравнение прямой:

Это линейная функция на интервале $x > 0$. Для построения графика подставим два значения для $x$:

• При $x = 0$:

  $$y = -2(0) = 0$$

• При $x = 1$:

  $$y = -2(1) = -2$$

Таким образом, на интервале $x > 0$ график будет прямой, которая проходит через точку $(0, 0)$ и имеет угловой коэффициент -2.

График функции:

График будет состоять из трех частей:

• Линейная часть $y = 2x + 2\pi$ для $x \leq -\pi$,
• Синусоида $y = \sin x$ для $-\pi < x \leq 0$,
• Линейная часть $y = -2x$ для $x > 0$.

Между этими частями будут разрывы в точках $x = -\pi$ и $x = 0$, так как функции не совпадают в этих точках.

в) Свойства функции:

Область определения $D(f)$:

Функция определена на всей числовой оси, так как для всех $x$ существует соответствующее выражение для $f(x)$. Таким образом, область определения:

$$D(f) = (-\infty; +\infty)$$

Множество значений $E(f)$:

Для каждого из кусочков функции:

• $f(x) = 2x + 2\pi$ на $(-\infty; -\pi]$ может принимать все значения от $-\infty$ до 0.
• $f(x) = \sin x$ на $(-\pi < x \leq 0)$ принимает значения от -1 до 0.
• $f(x) = -2x$ на $(0; +\infty)$ принимает все значения от 0 до $-\infty$.

Таким образом, функция всегда принимает значения $\leq 0$. Следовательно, множество значений:

$$E(f) = (-\infty; 0]$$

Возрастание и убывание функции:

• $f(x) = 2x + 2\pi$ возрастает на $(-\infty; -\pi]$,
• $f(x) = \sin x$ возрастает на $\left[-\frac{\pi}{2}; 0\right]$,
• $f(x) = -2x$ убывает на $[0; +\infty)$.

Функция возрастает на интервалах:

$$(-\infty; -\pi] \cup \left[-\frac{\pi}{2}; 0\right]$$

Убывание функции:
Функция убывает на интервалах:

$$\left[-\pi; -\frac{\pi}{2}\right] \cup [0; +\infty)$$

Значения функции $f(x) < 0$:

Функция принимает отрицательные значения на интервалах:

$$(-\infty; -\pi) \cup (-\pi; 0) \cup (0; +\infty)$$

Четность и нечетность:

Функция не является ни четной, ни нечетной:

• Она не симметрична относительно оси $y$ (нечетность),
• Она не симметрична относительно начала координат (четность).

Периодичность:

Функция не является периодической, так как она состоит из различных частей, каждая из которых имеет свою форму и поведение.