ГДЗ по Алгебре 10 Класс Номер 16.65 Профильный Уровень Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} -x^2, & \text{если } x < 0, \\ \sin x, & \text{если } 0 \leqslant x \leqslant \pi, \\ -(x — \pi)^2, & \text{если } x > \pi. \end{cases}$$

а) Вычислите: $f(-3)$, $f\left(\frac{\pi}{2}\right)$, $f(2\pi — 3)$;

б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

Дана функция:

$$f(x) = \begin{cases} -x^2, & \text{если } x < 0 \\ \sin x, & \text{если } 0 \leq x \leq \pi \\ -(x — \pi)^2, & \text{если } x > \pi \end{cases}$$

а) Найдем значения:

$$f(-3) = -(-3)^2 = -9;$$ $$f\left(\frac{\pi}{2}\right) = \sin \frac{\pi}{2} = 1;$$ $$f(2\pi — 3) = -(2\pi — 3 — \pi)^2 = -(\pi — 3)^2;$$

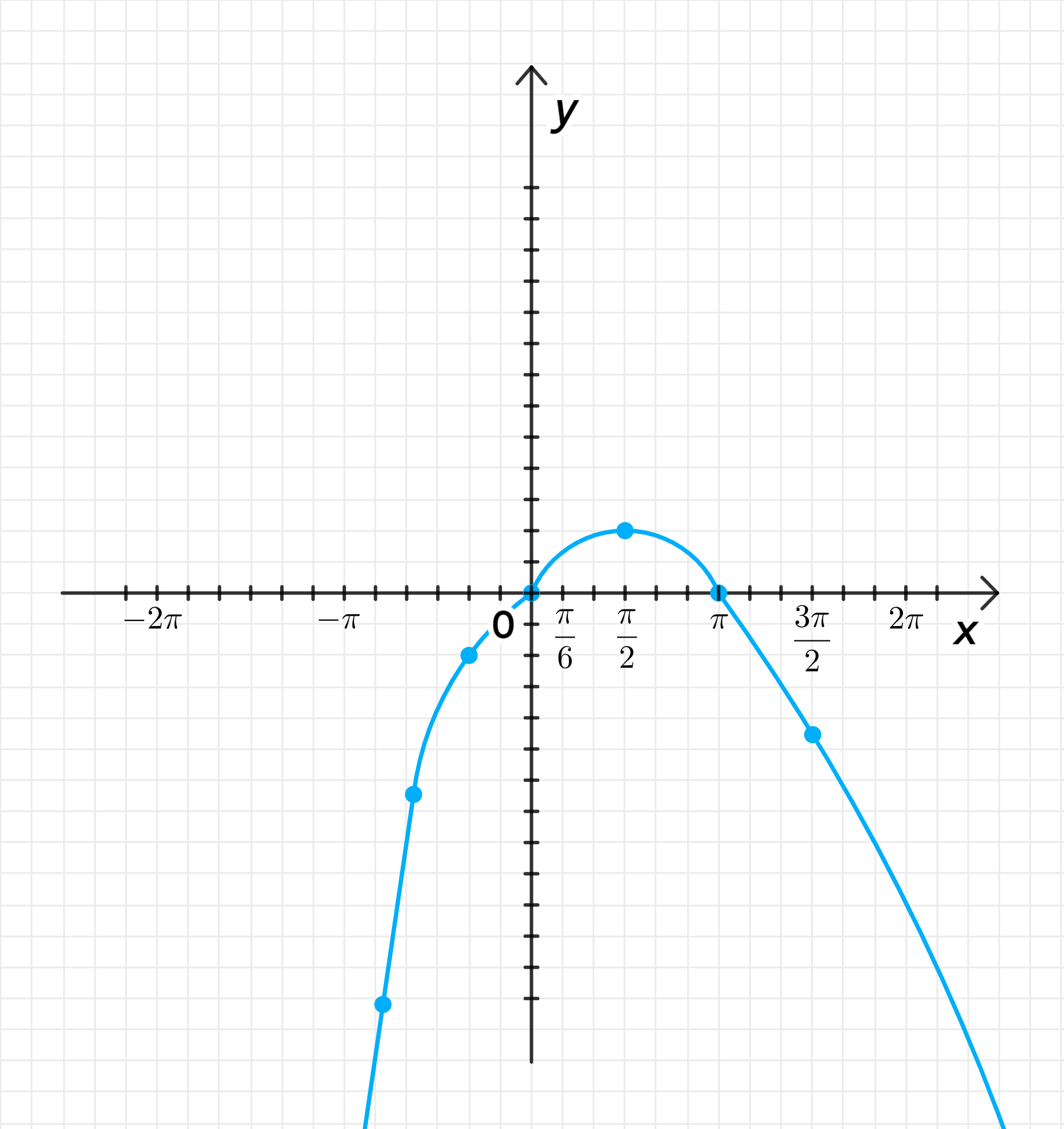
б) График функции:

$y = -x^2$ — уравнение параболы;
$x_0 = 0$, $y_0 = 0$;

$$\begin{array}{c|ccc} x & -2 & -1 & 0 \\ \hline y & -4 & -1 & 0 \\ \end{array}$$

$y = \sin x$ — уравнение синусоиды:

$$\begin{array}{c|ccc} x & 0 & \frac{\pi}{2} & \pi \\ \hline y & 0 & 1 & 0 \\ \end{array}$$

$y = -(x — \pi)^2$ — уравнение параболы;
$x_0 = \pi$, $y_0 = 0$;

$$\begin{array}{c|ccc} x & \pi & \frac{4\pi}{3} & \frac{3\pi}{2} \\ \hline y & 0 & \approx -1 & \approx -2.5 \\ \end{array}$$

Графики функций:

в) Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = (-\infty; 1]$;
• Возрастает на $\left( -\infty; \frac{\pi}{2} \right]$;
• Убывает на $\left[ \frac{\pi}{2}; +\infty \right)$;
• $f(x) > 0$ на $(0; \pi)$;
• $f(x) < 0$ на $(-\infty; 0) \cup (\pi; +\infty)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической

Дана функция:

$$f(x) = \begin{cases} -x^2, & \text{если } x < 0 \\ \sin x, & \text{если } 0 \leq x \leq \pi \\ -(x — \pi)^2, & \text{если } x > \pi \end{cases}$$

Эта функция является кусочно-заданной, то есть её определение зависит от того, в каком интервале лежит аргумент $x$. Мы будем рассматривать три случая, каждый из которых описан в отдельной части функции.

а) Найдем значения функции для различных аргументов.

1. Найдем $f(-3)$:

   Для $x = -3$ мы видим, что $x$ принадлежит интервалу $(-\infty, 0)$. В этом интервале функция определяется как $f(x) = -x^2$.

   $$f(-3) = -(-3)^2 = -(9) = -9$$

2. Найдем $f\left(\frac{\pi}{2}\right)$:

   Для $x = \frac{\pi}{2}$ мы видим, что $x$ лежит в интервале $[0, \pi]$, где функция определяется как $f(x) = \sin x$.

   $$f\left(\frac{\pi}{2}\right) = \sin \frac{\pi}{2} = 1$$

3. Найдем $f(2\pi — 3)$:

   Для $x = 2\pi — 3$ мы видим, что $x$ лежит в интервале $(\pi, +\infty)$, где функция определяется как $f(x) = -(x — \pi)^2$. Подставим значение $x = 2\pi — 3$:

   $$f(2\pi — 3) = -( (2\pi — 3) — \pi )^2 = -( (\pi — 3)^2 )$$

   Таким образом, получаем:

   $$f(2\pi — 3) = -(\pi — 3)^2$$

   Это выражение остаётся в такой форме, так как не требуется искать его числовое значение в этом контексте.

б) Построение графика функции.

График $y = -x^2$ (для $x < 0$):

Это уравнение параболы, направленной вниз, с вершиной в точке $(0, 0)$. Для более точного представления значений вычислим значения функции в нескольких точках:

$$\begin{array}{c|ccc} x & -2 & -1 & 0 \\ \hline y & -4 & -1 & 0 \\ \end{array}$$

Это подтверждает, что график является параболой, и в точке $x = 0$ он пересекает ось $x$.

График $y = \sin x$ (для $0 \leq x \leq \pi$):

Это уравнение синусоиды, которая начинается с нуля при $x = 0$, достигает максимума $1$ при $x = \frac{\pi}{2}$ и возвращается обратно к нулю при $x = \pi$. Рассмотрим несколько точек:

$$\begin{array}{c|ccc} x & 0 & \frac{\pi}{2} & \pi \\ \hline y & 0 & 1 & 0 \\ \end{array}$$

График $y = -(x — \pi)^2$ (для $x > \pi$):

Это уравнение параболы, направленной вниз, с вершиной в точке $(\pi, 0)$. Рассмотрим несколько точек для построения графика:

$$\begin{array}{c|ccc} x & \pi & \frac{4\pi}{3} & \frac{3\pi}{2} \\ \hline y & 0 & \approx -1 & \approx -2.5 \\ \end{array}$$

Здесь видим, что функция убывает после $x = \pi$.

График всей функции:

в) Свойства функции.

Область определения (Domain):

Область определения функции $D(f)$ — это все значения $x$, для которых функция определена. Поскольку в каждом из трёх случаев функция задана для всех $x$ на своём интервале, область определения будет:

$$D(f) = (-\infty; +\infty)$$

Множество значений (Range):

Для каждого из интервалов определим множество значений функции:

• На интервале $(-\infty, 0)$ функция $f(x) = -x^2$ принимает значения от $0$ до $-\infty$.
• На интервале $[0, \pi]$ функция $f(x) = \sin x$ принимает значения от $0$ до $1$.
• На интервале $(\pi, +\infty)$ функция $f(x) = -(x — \pi)^2$ принимает значения от $0$ до $-\infty$.

Объединяя все эти интервалы, получаем:

$$E(f) = (-\infty; 1]$$

Монотонность:

• Функция возрастает на интервале $(-\infty, \frac{\pi}{2}]$, потому что для значений $x$ из этого интервала функция $f(x) = -x^2$ убывает, а $\sin x$ возрастает.
• Функция убывает на интервале $[\frac{\pi}{2}, +\infty)$, так как на интервале $[0, \pi]$ синусоида убывает от $1$ к $0$, а вторая парабола $-(x — \pi)^2$ убывает.

Знаки функции:

• $f(x) > 0$ на интервале $(0, \pi)$, где синус положителен.
• $f(x) < 0$ на интервалах $(-\infty, 0) \cup (\pi, +\infty)$, где либо параболы, либо синус отрицателен.

Четность и нечетность:

Функция не является чётной, так как для чётности $f(-x)$ должно быть равно $f(x)$, что здесь не выполняется. Также функция не является нечётной, так как для нечётности $f(-x) = -f(x)$, чего также не происходит.

Периодичность:

Функция не является периодической, так как её график не повторяется с каким-либо периодом.