ГДЗ по Алгебре 10 Класс Номер 16.67 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \frac{1}{\sin x}$;

б) $y = \frac{1}{\cos x}$

а) $y = \frac{1}{\sin x}$;

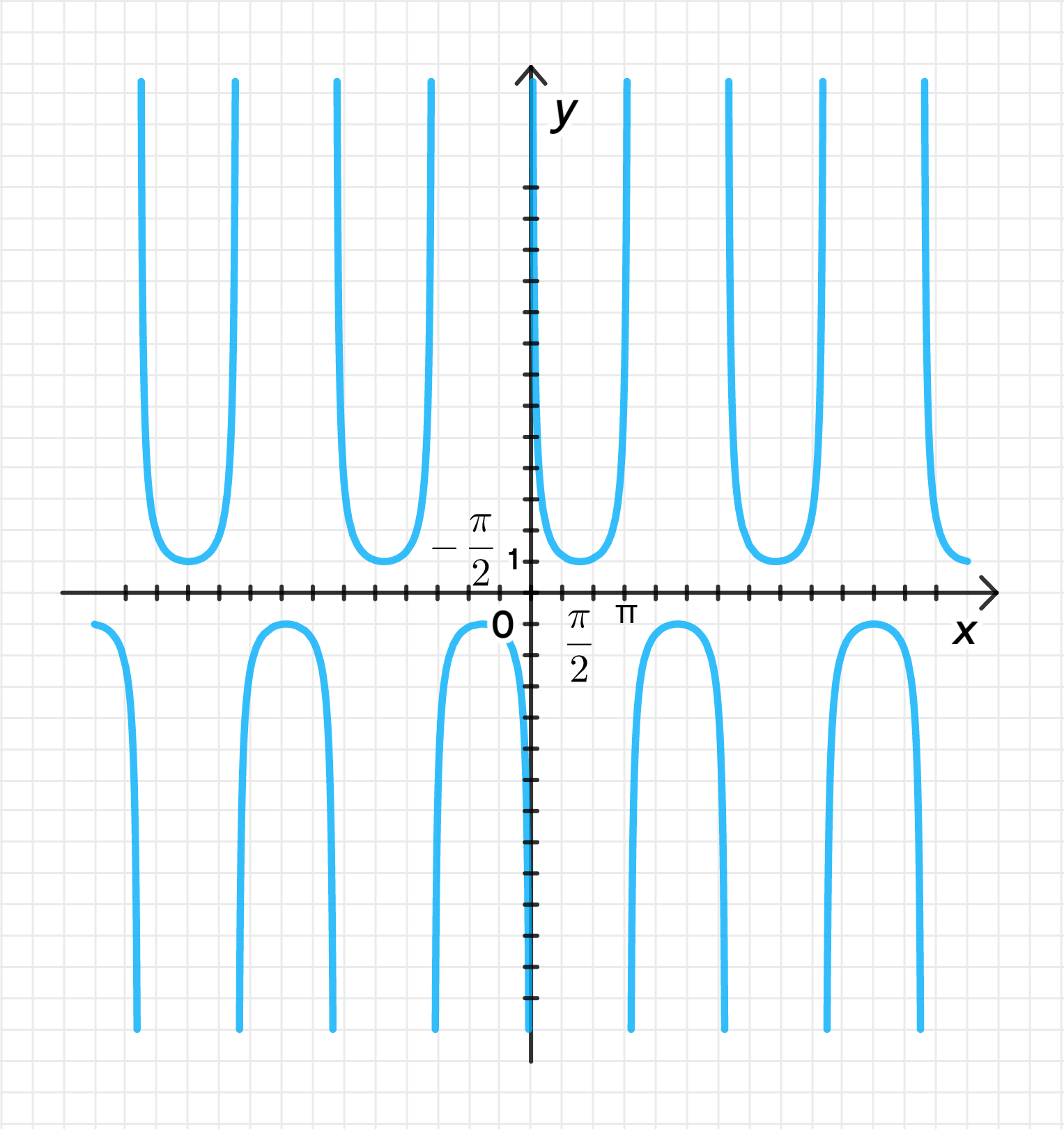
Функция является нечетной:

$$y(-x) = \frac{1}{\sin(-x)} = -\frac{1}{\sin x} = -y(x);$$

Выражение имеет смысл при:

$$\sin x \neq 0;$$ $$x \neq \pi n;$$

Если $0 < x \leq \frac{\pi}{2}$, тогда:

$$y = \sin x — \text{возрастает};$$ $$y = \frac{1}{\sin x} — \text{убывает};$$

Если $\frac{\pi}{2} \leq x < \pi$, тогда:

$$y = \sin x — \text{убывает};$$ $$y = \frac{1}{\sin x} — \text{возрастает};$$

На двух данных отрезках:

$$0 < \sin x \leq 1;$$ $$1 \leq \frac{1}{\sin x} < +\infty;$$

График функции:

б) $y = \frac{1}{\cos x}$;

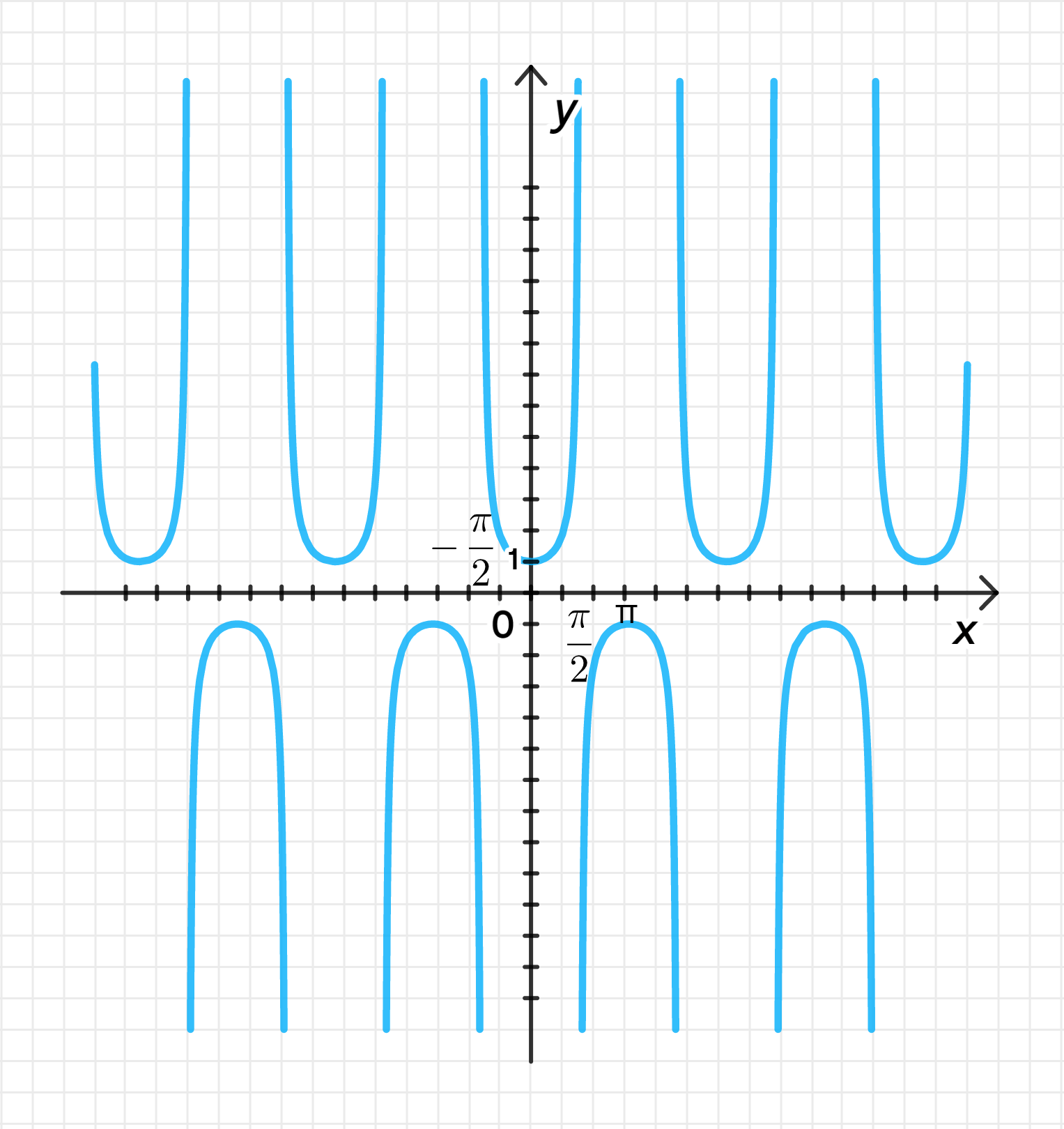
Функция является четной:

$$y(-x) = \frac{1}{\cos(-x)} = \frac{1}{\cos x} = y(x);$$

Выражение имеет смысл при:

$$\cos x \neq 0;$$ $$x \neq \pm \frac{\pi}{2} + 2\pi n;$$

Если $0 \leq x < \frac{\pi}{2}$, тогда:

$$0 < \cos x \leq 1;$$ $$1 \leq \frac{1}{\cos x} < +\infty;$$

Если $\frac{\pi}{2} \leq x \leq \pi$, тогда:

$$-1 \leq \cos x < 0;$$ $$-1 \leq \frac{1}{\cos x} < -\infty;$$

На двух данных отрезках:

$$y = \cos x — \text{убывает};$$ $$y = \frac{1}{\cos x} — \text{возрастает};$$

График функции:

а) $y = \frac{1}{\sin x}$

1. Функция является нечетной:

Чтобы доказать, что функция $y = \frac{1}{\sin x}$ нечетная, нужно показать, что для всех $x$ выполняется следующее равенство:

$$y(-x) = -y(x)$$

Проверим:

$$y(-x) = \frac{1}{\sin(-x)} = \frac{1}{-\sin x} = -\frac{1}{\sin x} = -y(x)$$

Таким образом, функция является нечетной, так как выполняется условие $y(-x) = -y(x)$.

2. Выражение имеет смысл при $\sin x \neq 0$:

Функция $y = \frac{1}{\sin x}$ имеет смысл, только если знаменатель не равен нулю. То есть:

$$\sin x \neq 0$$

Значение синуса равно нулю при $x = n\pi$, где $n$ — целое число. Следовательно, функция имеет смысл при:

$$x \neq n\pi$$

где $n \in \mathbb{Z}$.

3. Поведение функции на интервале $0 < x \leq \frac{\pi}{2}$:

Для интервала $0 < x \leq \frac{\pi}{2}$:

• $\sin x$ возрастает от 0 до 1.
• Таким образом, $\frac{1}{\sin x}$ убывает, так как значение синуса увеличивается, а его обратная величина уменьшается.

Значит:

• Функция $y = \sin x$ возрастает на этом интервале.
• Функция $y = \frac{1}{\sin x}$ убывает на этом интервале.

4. Поведение функции на интервале $\frac{\pi}{2} \leq x < \pi$:

Для интервала $\frac{\pi}{2} \leq x < \pi$:

• $\sin x$ убывает от 1 до 0.
• Таким образом, $\frac{1}{\sin x}$ возрастает, так как значение синуса убывает, а его обратная величина увеличивается.

Значит:

• Функция $y = \sin x$ убывает на этом интервале.
• Функция $y = \frac{1}{\sin x}$ возрастает на этом интервале.

5. Значения функции на данных отрезках:

• На интервале $0 < x \leq \frac{\pi}{2}$, $\sin x$ принимает значения от 0 до 1 (не включая 0). Следовательно, $\frac{1}{\sin x}$ принимает значения от 1 до $+\infty$.

  Таким образом:

  $$0 < \sin x \leq 1 \quad \text{и} \quad 1 \leq \frac{1}{\sin x} < +\infty$$

• На интервале $\frac{\pi}{2} \leq x < \pi$, $\sin x$ принимает значения от 1 до 0 (не включая 0). Следовательно, $\frac{1}{\sin x}$ снова принимает значения от $+\infty$ до 1.

6. График функции:

б) $y = \frac{1}{\cos x}$

1. Функция является четной:

Для доказательства четности функции нужно показать, что для всех $x$ выполняется следующее равенство:

$$y(-x) = y(x)$$

Проверим:

$$y(-x) = \frac{1}{\cos(-x)} = \frac{1}{\cos x} = y(x)$$

Таким образом, функция является четной, так как выполняется условие $y(-x) = y(x)$.

2. Выражение имеет смысл при $\cos x \neq 0$:

Функция $y = \frac{1}{\cos x}$ имеет смысл, только если знаменатель не равен нулю. То есть:

$$\cos x \neq 0$$

Значение косинуса равно нулю при $x = \frac{\pi}{2} + n\pi$, где $n$ — целое число. Следовательно, функция имеет смысл при:

$$x \neq \pm \frac{\pi}{2} + 2\pi n$$

где $n \in \mathbb{Z}$.

3. Поведение функции на интервале $0 \leq x < \frac{\pi}{2}$:

Для интервала $0 \leq x < \frac{\pi}{2}$:

• $\cos x$ возрастает от 0 до 1.
• Таким образом, $\frac{1}{\cos x}$ убывает, так как значение косинуса увеличивается, а его обратная величина уменьшается.

Значит:

• Функция $y = \cos x$ убывает на этом интервале.
• Функция $y = \frac{1}{\cos x}$ возрастает на этом интервале.

4. Поведение функции на интервале $\frac{\pi}{2} \leq x \leq \pi$:

Для интервала $\frac{\pi}{2} \leq x \leq \pi$:

• $\cos x$ убывает от 0 до -1.
• Таким образом, $\frac{1}{\cos x}$ возрастает, так как значение косинуса убывает, а его обратная величина увеличивается.

Значит:

• Функция $y = \cos x$ убывает на этом интервале.
• Функция $y = \frac{1}{\cos x}$ возрастает на этом интервале.

5. Значения функции на данных отрезках:

• На интервале $0 \leq x < \frac{\pi}{2}$, $\cos x$ принимает значения от 1 до 0 (не включая 0). Следовательно, $\frac{1}{\cos x}$ принимает значения от 1 до $+\infty$.

  Таким образом:

  $$0 < \cos x \leq 1 \quad \text{и} \quad 1 \leq \frac{1}{\cos x} < +\infty$$

• На интервале $\frac{\pi}{2} \leq x \leq \pi$, $\cos x$ принимает значения от 0 до -1. Следовательно, $\frac{1}{\cos x}$ принимает значения от $-\infty$ до -1.

6. График функции: