Краткий ответ:
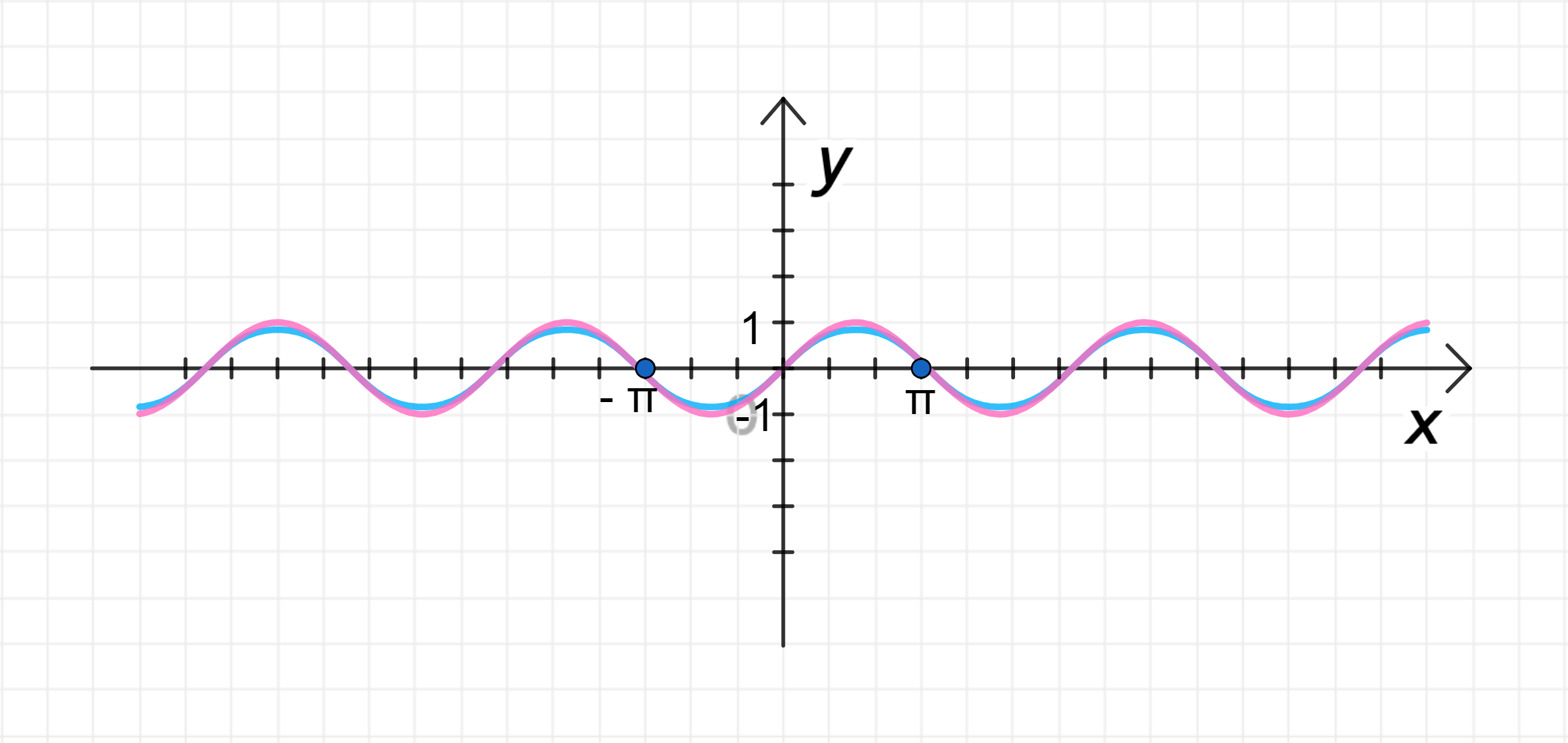
а) y = sin x ( sin x ) y = \sin x (\sin x)
Функция является нечетной:
y ( − x ) = sin ( sin ( − x ) ) = sin ( − sin x ) = − sin ( sin x ) = − y ( x ) ; y(-x) = \sin(\sin(-x)) = \sin(-\sin x) = -\sin(\sin x) = -y(x);
Значения функции:
y ( 0 ) = sin ( sin 0 ) = sin 0 = 0 ; y(0) = \sin(\sin 0) = \sin 0 = 0; y ( π 2 ) = sin ( sin π 2 ) = sin 1 ≈ sin π 3 ≈ 3 2 ≈ 0 , 85 ; y\left(\frac{\pi}{2}\right) = \sin\left(\sin\frac{\pi}{2}\right) = \sin 1 \approx \sin\frac{\pi}{3} \approx \frac{\sqrt{3}}{2} \approx 0,85; y ( π ) = sin ( sin π ) = sin 0 = 0 ; y(\pi) = \sin(\sin \pi) = \sin 0 = 0;
График функции:
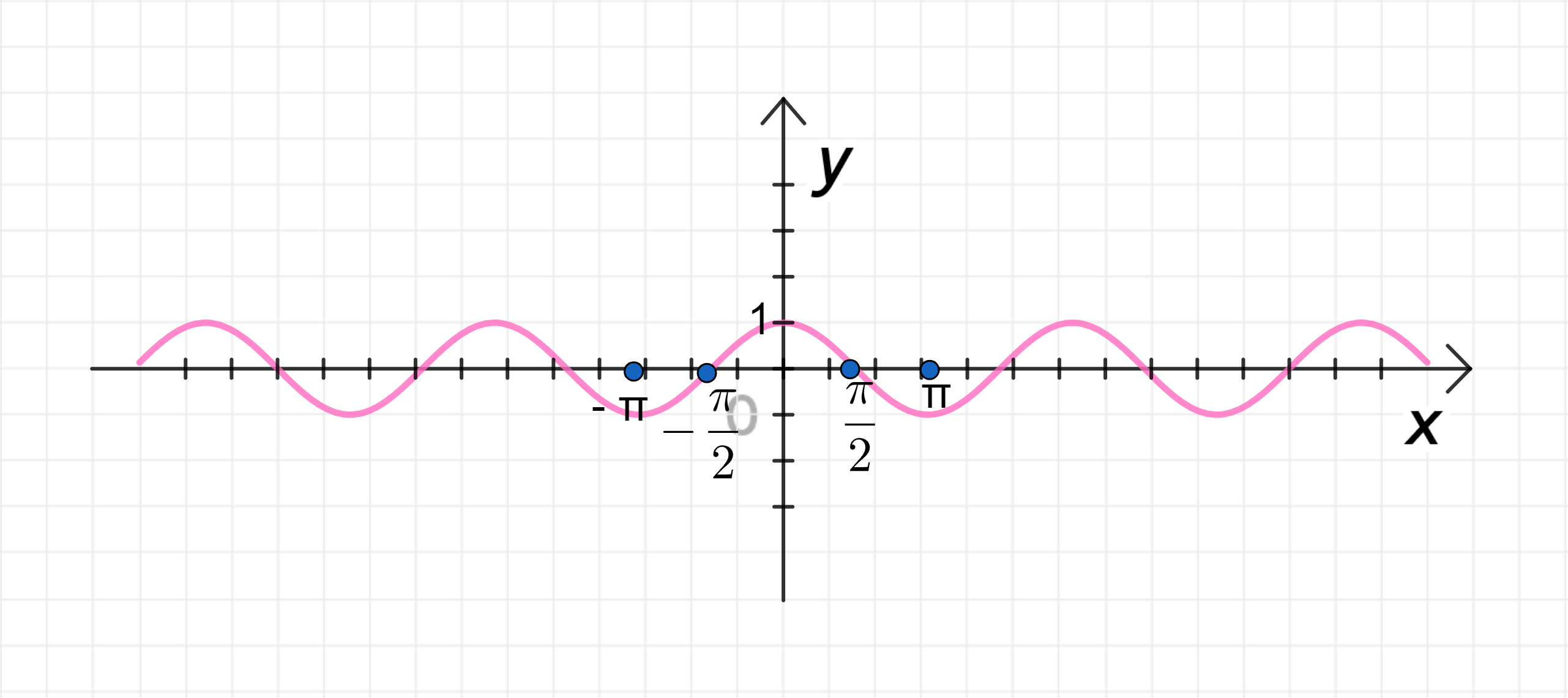
б) y = sin x ( cos x ) y = \sin x (\cos x)
Функция является четной:
y ( − x ) = sin ( cos ( − x ) ) = sin ( cos x ) = y ( x ) ; y(-x) = \sin(\cos(-x)) = \sin(\cos x) = y(x);
Значения функции:
y ( 0 ) = sin ( cos 0 ) = sin 1 ≈ sin π 3 ≈ 3 2 ≈ 0 , 85 ; y(0) = \sin(\cos 0) = \sin 1 \approx \sin\frac{\pi}{3} \approx \frac{\sqrt{3}}{2} \approx 0,85; y ( π 2 ) = sin ( cos π 2 ) = sin 0 = 0 ; y\left(\frac{\pi}{2}\right) = \sin\left(\cos\frac{\pi}{2}\right) = \sin 0 = 0; y ( π ) = sin ( cos π ) = sin ( − 1 ) = − sin 1 ≈ − 0 , 85 ; y(\pi) = \sin(\cos \pi) = \sin(-1) = -\sin 1 \approx -0,85;
График функции:
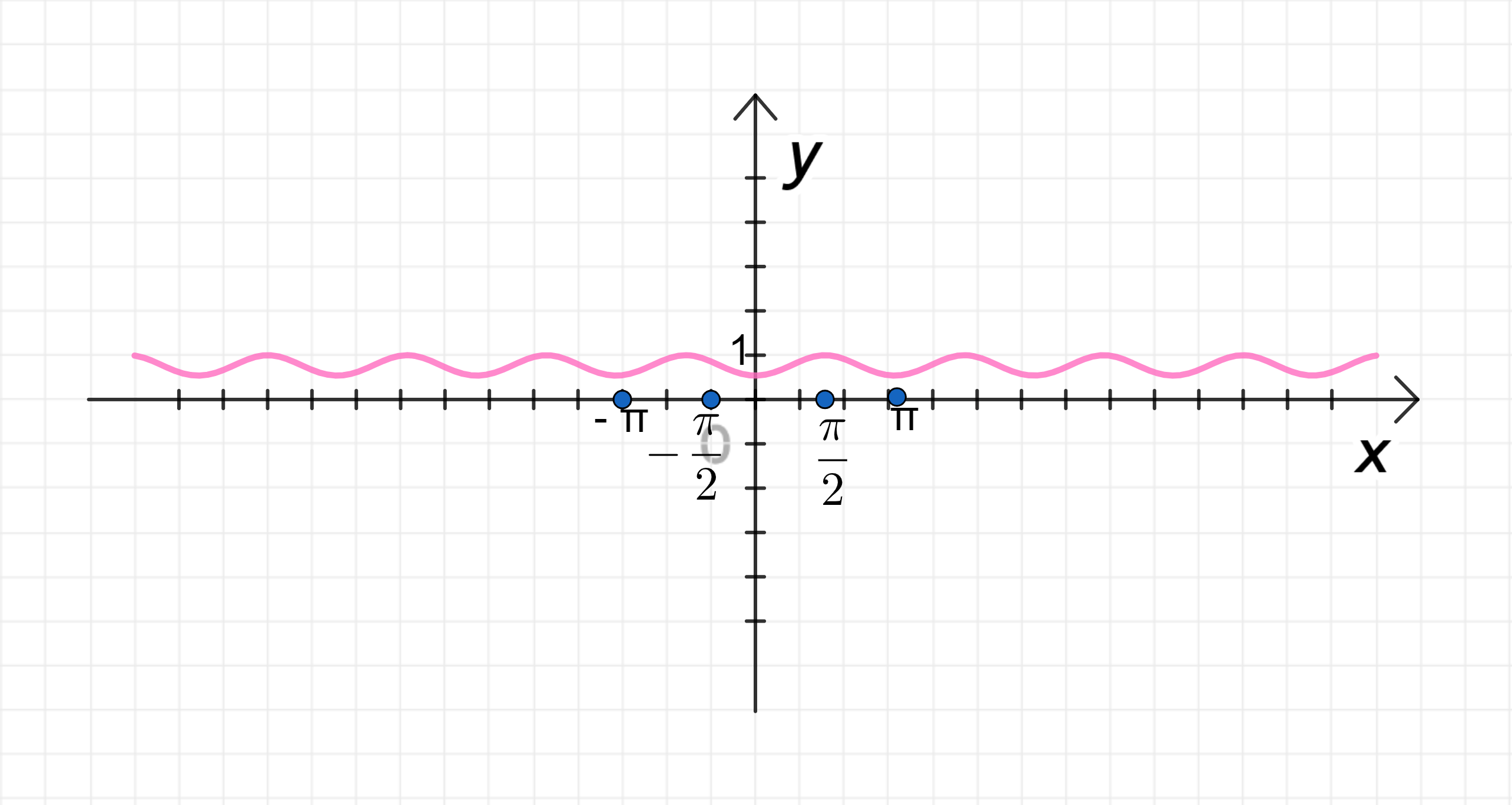
в) y = cos x ( cos x ) y = \cos x (\cos x)
Функция является четной:
y ( − x ) = cos ( cos ( − x ) ) = cos ( cos x ) = y ( x ) ; y(-x) = \cos(\cos(-x)) = \cos(\cos x) = y(x);
Значения функции:
y ( 0 ) = cos ( cos 0 ) = cos 1 ≈ cos π 3 ≈ 0 , 5 ; y(0) = \cos(\cos 0) = \cos 1 \approx \cos\frac{\pi}{3} \approx 0,5; y ( π 2 ) = cos ( cos π 2 ) = cos 0 = 1 ; y\left(\frac{\pi}{2}\right) = \cos\left(\cos\frac{\pi}{2}\right) = \cos 0 = 1; y ( π ) = cos ( cos π ) = cos ( − 1 ) = cos 1 ≈ 0 , 5 ; y(\pi) = \cos(\cos \pi) = \cos(-1) = \cos 1 \approx 0,5;
График функции:
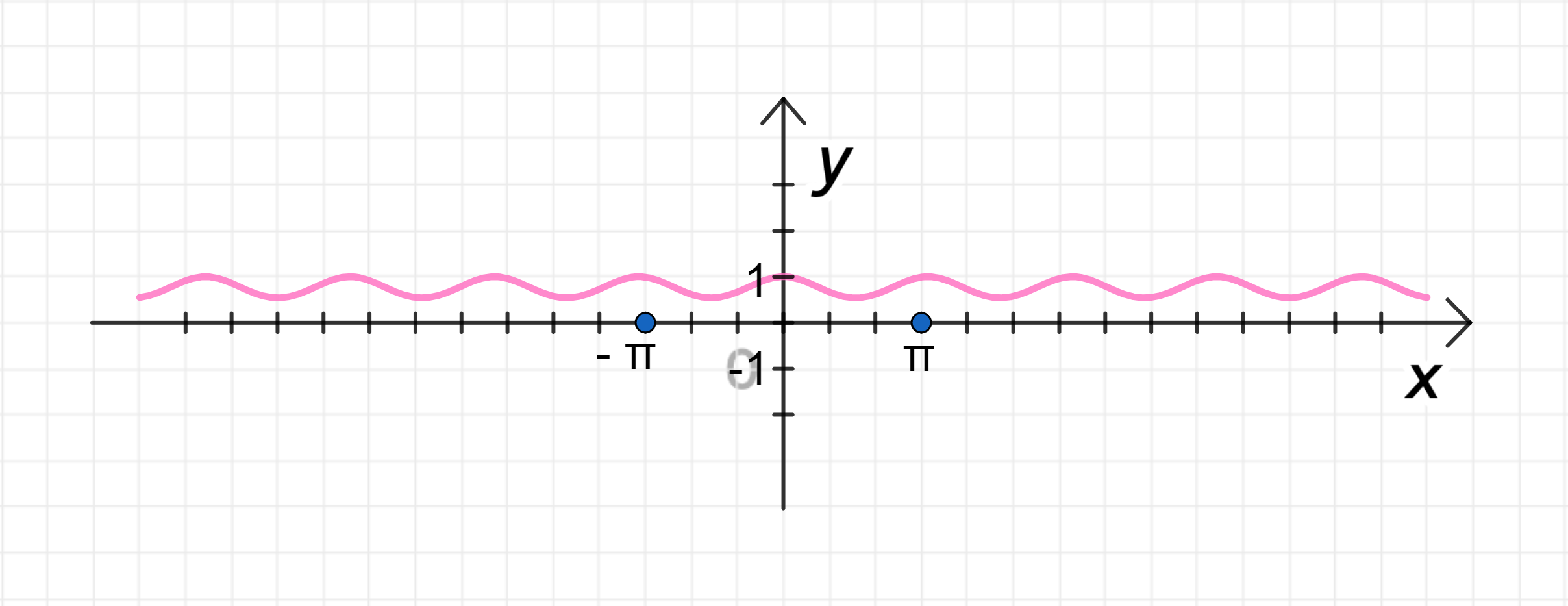
г) y = cos x ( sin x ) y = \cos x (\sin x)
Функция является четной:
y ( − x ) = cos ( sin ( − x ) ) = cos ( − sin x ) = cos ( sin x ) = y ( x ) ; y(-x) = \cos(\sin(-x)) = \cos(-\sin x) = \cos(\sin x) = y(x);
Значения функции:
y ( 0 ) = cos ( sin 0 ) = cos 0 = 1 ; y(0) = \cos(\sin 0) = \cos 0 = 1; y ( π 2 ) = cos ( sin π 2 ) = cos 1 ≈ cos π 3 ≈ 0 , 5 ; y\left(\frac{\pi}{2}\right) = \cos\left(\sin\frac{\pi}{2}\right) = \cos 1 \approx \cos\frac{\pi}{3} \approx 0,5; y ( π ) = cos ( sin π ) = cos 0 = 1 ; y(\pi) = \cos(\sin \pi) = \cos 0 = 1;
График функции:
Подробный ответ:
а) y = sin ( sin x ) y = \sin(\sin x)
1) Функция является нечетной:
Чтобы доказать, что функция является нечетной, нужно показать, что выполняется следующее равенство для всех значений x x
y ( − x ) = − y ( x ) y(-x) = -y(x)
Рассмотрим:
y ( − x ) = sin ( sin ( − x ) ) = sin ( − sin x ) y(-x) = \sin(\sin(-x)) = \sin(-\sin x)
Поскольку синус — нечетная функция, то sin ( − x ) = − sin x \sin(-x) = -\sin x
y ( − x ) = sin ( − sin x ) = − sin ( sin x ) y(-x) = \sin(-\sin x) = -\sin(\sin x)
Таким образом, мы получаем:
y ( − x ) = − y ( x ) y(-x) = -y(x)
Значит, функция y = sin ( sin x ) y = \sin(\sin x)
2) Значения функции:
Теперь найдем значения функции в некоторых точках:
При x = 0 x = 0 y ( 0 ) = sin ( sin 0 ) = sin ( 0 ) = 0 y(0) = \sin(\sin 0) = \sin(0) = 0
Таким образом, y ( 0 ) = 0 y(0) = 0
При x = π 2 x = \frac{\pi}{2} y ( π 2 ) = sin ( sin π 2 ) = sin ( 1 ) y\left(\frac{\pi}{2}\right) = \sin\left(\sin\frac{\pi}{2}\right) = \sin(1)
Так как sin π 2 = 1 \sin\frac{\pi}{2} = 1
y ( π 2 ) ≈ sin ( 1 ) ≈ 0 , 841 y\left(\frac{\pi}{2}\right) \approx \sin(1) \approx 0,841
При x = π x = \pi y ( π ) = sin ( sin π ) = sin ( 0 ) = 0 y(\pi) = \sin(\sin \pi) = \sin(0) = 0
Таким образом, y ( π ) = 0 y(\pi) = 0
3) График функции:
б) y = sin ( cos x ) y = \sin(\cos x)
1) Функция является четной:
Чтобы доказать, что функция является четной, необходимо проверить, что для всех значений x x
y ( − x ) = y ( x ) y(-x) = y(x)
Рассмотрим:
y ( − x ) = sin ( cos ( − x ) ) = sin ( cos x ) y(-x) = \sin(\cos(-x)) = \sin(\cos x)
Поскольку cos ( − x ) = cos x \cos(-x) = \cos x
y ( − x ) = sin ( cos x ) = y ( x ) y(-x) = \sin(\cos x) = y(x)
Таким образом, функция y = sin ( cos x ) y = \sin(\cos x)
2) Значения функции:
Теперь найдем значения функции в некоторых точках:
При x = 0 x = 0 y ( 0 ) = sin ( cos 0 ) = sin ( 1 ) y(0) = \sin(\cos 0) = \sin(1)
Приближенно это:
y ( 0 ) ≈ 0 , 841 y(0) \approx 0,841
При x = π 2 x = \frac{\pi}{2} y ( π 2 ) = sin ( cos π 2 ) = sin ( 0 ) = 0 y\left(\frac{\pi}{2}\right) = \sin\left(\cos\frac{\pi}{2}\right) = \sin(0) = 0
Таким образом, y ( π 2 ) = 0 y\left(\frac{\pi}{2}\right) = 0
При x = π x = \pi y ( π ) = sin ( cos π ) = sin ( − 1 ) y(\pi) = \sin(\cos \pi) = \sin(-1)
Это приближенно равно:
y ( π ) ≈ − sin ( 1 ) ≈ − 0 , 841 y(\pi) \approx -\sin(1) \approx -0,841
3) График функции:
в) y = cos ( cos x ) y = \cos(\cos x)
1) Функция является четной:
Чтобы доказать, что функция является четной, нужно показать, что для всех значений x x
y ( − x ) = y ( x ) y(-x) = y(x)
Рассмотрим:
y ( − x ) = cos ( cos ( − x ) ) = cos ( cos x ) y(-x) = \cos(\cos(-x)) = \cos(\cos x)
Поскольку cos ( − x ) = cos x \cos(-x) = \cos x
y ( − x ) = cos ( cos x ) = y ( x ) y(-x) = \cos(\cos x) = y(x)
Таким образом, функция y = cos ( cos x ) y = \cos(\cos x)
2) Значения функции:
Теперь найдем значения функции в некоторых точках:
При x = 0 x = 0 y ( 0 ) = cos ( cos 0 ) = cos ( 1 ) y(0) = \cos(\cos 0) = \cos(1)
Приближенно это:
y ( 0 ) ≈ 0 , 540 y(0) \approx 0,540
При x = π 2 x = \frac{\pi}{2} y ( π 2 ) = cos ( cos π 2 ) = cos ( 0 ) = 1 y\left(\frac{\pi}{2}\right) = \cos\left(\cos\frac{\pi}{2}\right) = \cos(0) = 1
При x = π x = \pi y ( π ) = cos ( cos π ) = cos ( − 1 ) y(\pi) = \cos(\cos \pi) = \cos(-1)
Это приближенно равно:
y ( π ) ≈ cos ( 1 ) ≈ 0 , 540 y(\pi) \approx \cos(1) \approx 0,540
3) График функции:
г) y = cos ( sin x ) y = \cos(\sin x)
1) Функция является четной:
Чтобы доказать, что функция является четной, нужно показать, что для всех значений x x
y ( − x ) = y ( x ) y(-x) = y(x)
Рассмотрим:
y ( − x ) = cos ( sin ( − x ) ) = cos ( − sin x ) y(-x) = \cos(\sin(-x)) = \cos(-\sin x)
Поскольку косинус — четная функция, то cos ( − sin x ) = cos ( sin x ) \cos(-\sin x) = \cos(\sin x)
y ( − x ) = y ( x ) y(-x) = y(x)
Значит, функция y = cos ( sin x ) y = \cos(\sin x)
2) Значения функции:
Теперь найдем значения функции в некоторых точках:
При x = 0 x = 0 y ( 0 ) = cos ( sin 0 ) = cos ( 0 ) = 1 y(0) = \cos(\sin 0) = \cos(0) = 1
При x = π 2 x = \frac{\pi}{2} y ( π 2 ) = cos ( sin π 2 ) = cos ( 1 ) y\left(\frac{\pi}{2}\right) = \cos\left(\sin\frac{\pi}{2}\right) = \cos(1)
Приближенно это:
y ( π 2 ) ≈ 0 , 540 y\left(\frac{\pi}{2}\right) \approx 0,540
При x = π x = \pi y ( π ) = cos ( sin π ) = cos ( 0 ) = 1 y(\pi) = \cos(\sin \pi) = \cos(0) = 1
3) График функции: