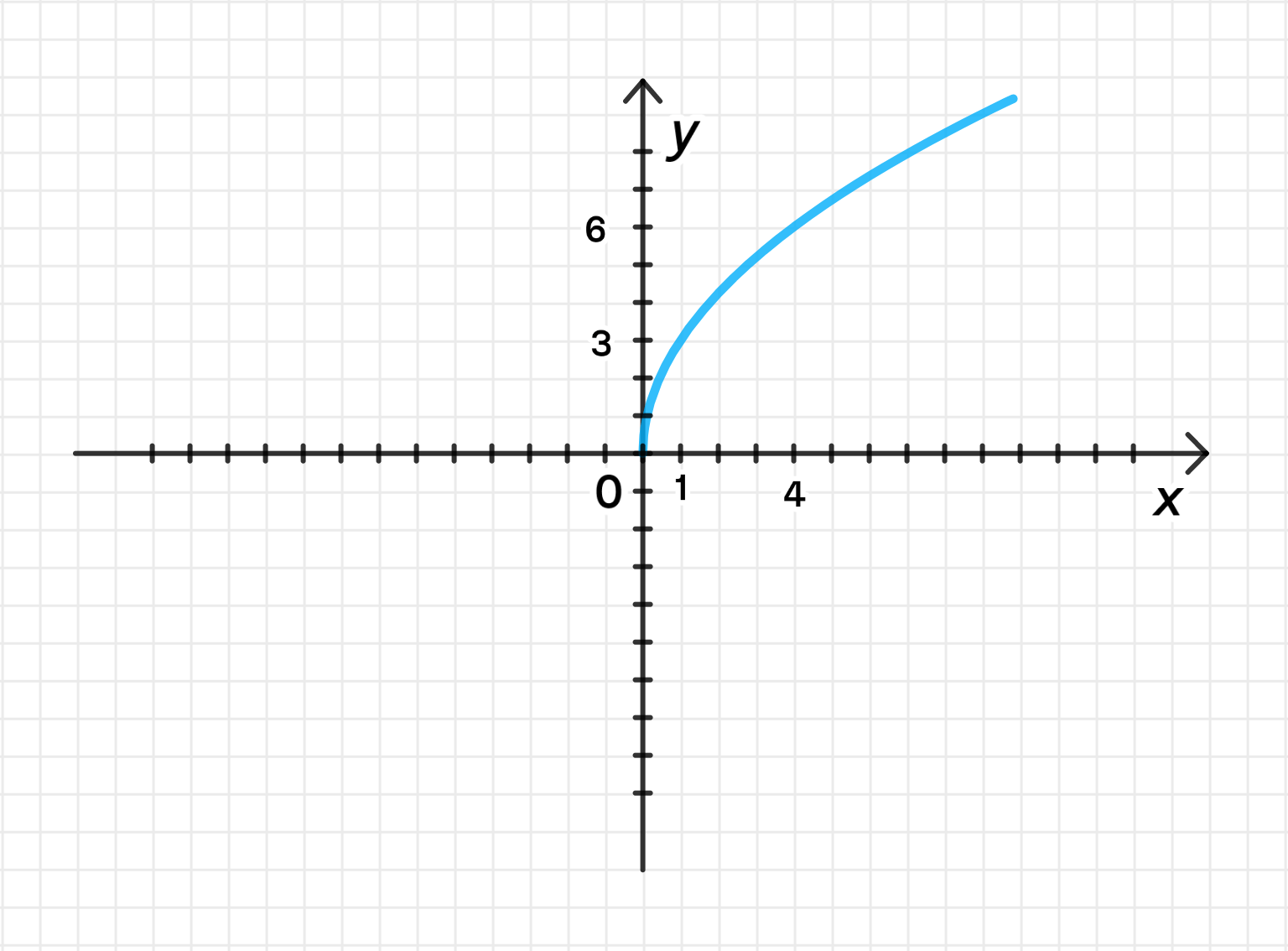Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 17.1 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а) ;
б) ;
в) ;
г)
а) ;
Построим график функции :
| 0 | 1 | 4 | 9 | |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 |
Совершим растяжение графика от оси с коэффициентом :
б) ;
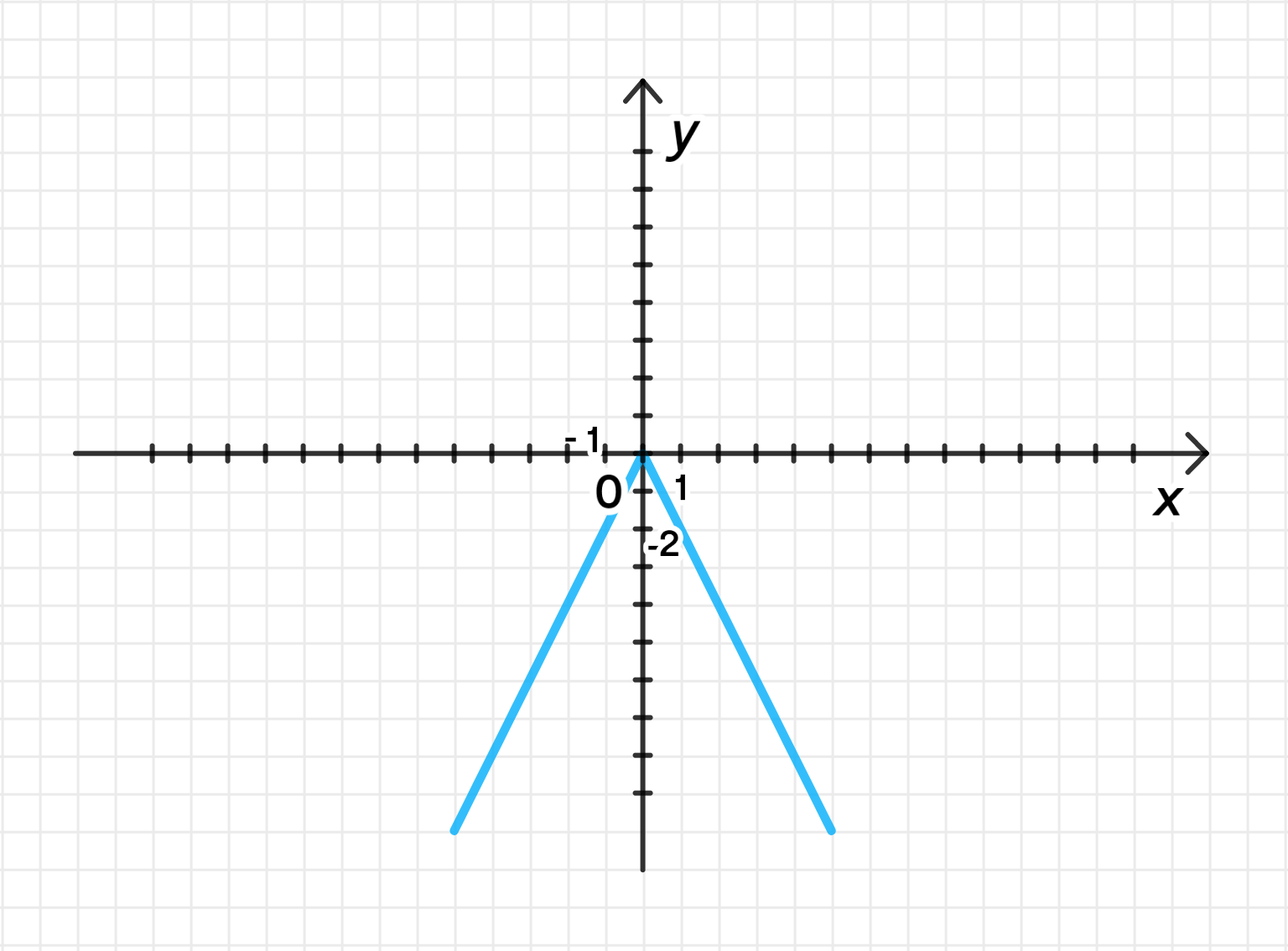
Построим график функции :
| -1 | 0 | 1 | |
|---|---|---|---|
| 1 | 0 | 1 |
Отразим график относительно оси абсцисс;
Совершим растяжение графика от оси с коэффициентом :
в) ;
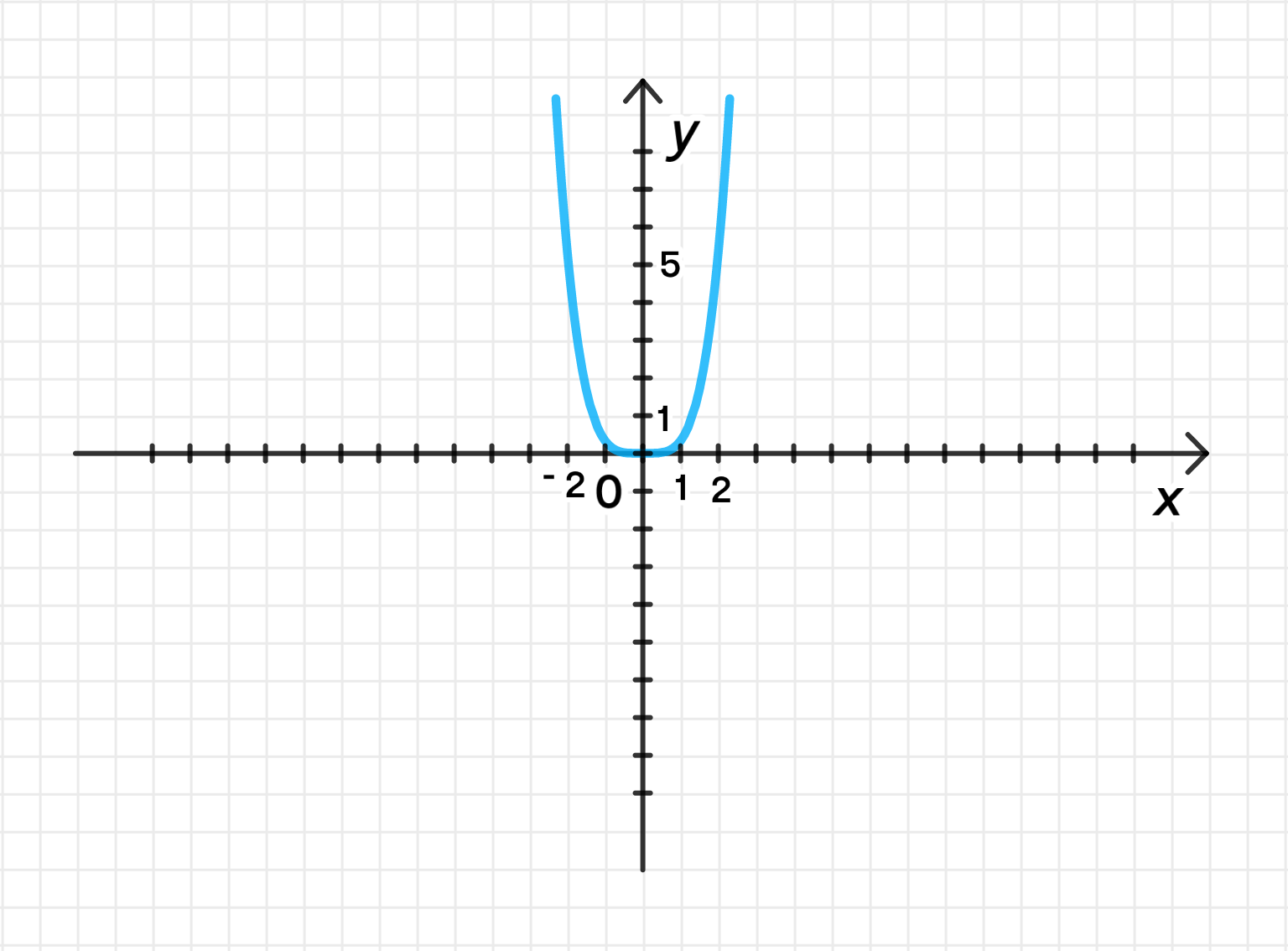
Построим график функции :
| -2 | -1 | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| 16 | 1 | 0 | 1 | 16 |
Совершим сжатие графика к оси с коэффициентом :
г) ;
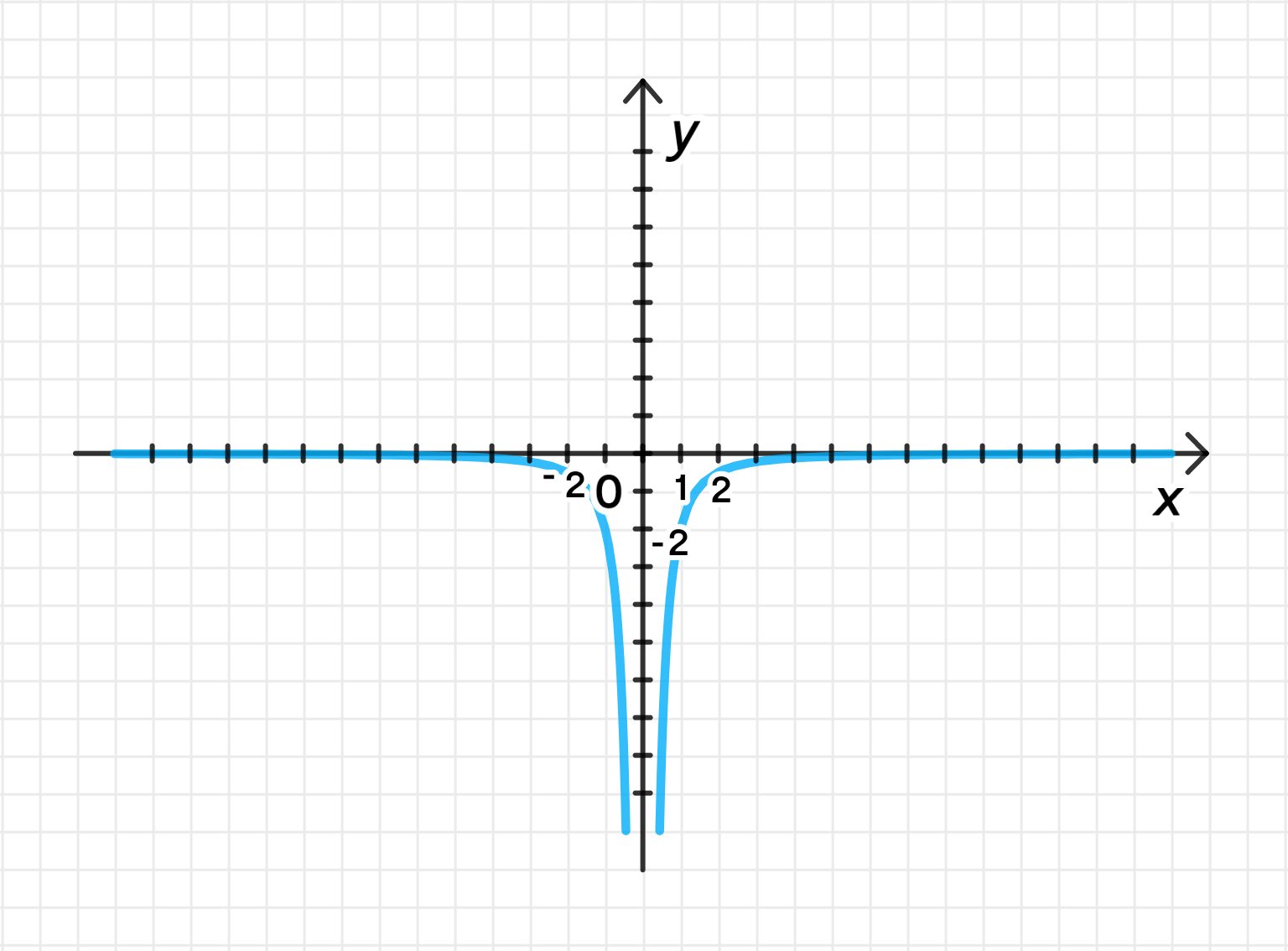
Построим график функции :
| -2 | -1 | -0.5 | 0.5 | 1 | 2 | |
|---|---|---|---|---|---|---|
| 0.25 | 1 | 4 | 4 | 1 | 0.25 |
Отразим график относительно оси абсцисс;
Совершим растяжение графика от оси с коэффициентом :
а)
1) Построим график функции
Функция определена для , так как извлечение квадратного корня из отрицательных чисел невозможно в области действительных чисел.
Рассмотрим несколько значений и соответствующие значения :
| 0 | 1 | 4 | 9 | |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 |
Так как , то значения растут с увеличением . График этой функции будет представлять собой растущую кривую, начинающуюся от точки и направляющуюся вправо.
2) Совершим растяжение графика от оси с коэффициентом
Теперь для каждого значения умножим его на 3, получив новую функцию . Это означает, что каждый на графике функции будет увеличен в 3 раза.
Для вычислений, если для для значение , то для новой функции значение .
График этой функции будет растянут в 3 раза по оси по сравнению с графиком функции . Таким образом, каждая точка на графике будет перемещена вверх, увеличив значение на коэффициент 3.
б)
1) Построим график функции
График функции представляет собой букву «V», которая симметрична относительно оси . Функция определена для всех , и ее значения всегда положительны или равны нулю.
Рассмотрим несколько значений и соответствующие значения :
| -1 | 0 | 1 | |
|---|---|---|---|
| 1 | 0 | 1 |
Так как , то для всех значений график будет либо на оси , либо выше этой оси.
2) Отразим график относительно оси абсцисс
Отражение графика относительно оси абсцисс означает, что мы заменяем на . То есть, значения функции становятся отрицательными для всех .
Таким образом, для графика все значения будут зеркально отражены вниз.
3) Совершим растяжение графика от оси с коэффициентом
Теперь каждый -координат будет умножен на 2. Если для значение при равно -1, то для функции это значение будет . Это означает, что график будет растянут в 2 раза по оси .
График станет более «крутым», и буква «V» будет вытянута вниз в два раза по сравнению с графиком .
в)
1) Построим график функции
График функции представляет собой четную функцию (симметричен относительно оси ), и для , . Для положительных значений функция растет, а для отрицательных значений функция также растет (так как четная степень исключает знак).
Рассмотрим несколько значений и соответствующие значения :
| -2 | -1 | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| 16 | 1 | 0 | 1 | 16 |
Таким образом, для больших значения функции растут очень быстро. Это будет парабола, «развернутая» вверх.
2) Совершим сжатие графика к оси с коэффициентом
Теперь умножим все значения функции на , что приведет к сжатию графика по оси . Каждый будет уменьшен в 3 раза. Если для функции при значение , то для новой функции значение будет .
Это означает, что график станет менее крутым по сравнению с исходным графиком , сжмется вертикально на коэффициент .
г)
1) Построим график функции
График функции является гиперболой. Он определен для всех , и значение всегда положительно. При функция не определена, а при значение функции стремится к нулю.
Рассмотрим несколько значений и соответствующие значения :
| -2 | -1 | -0.5 | 0.5 | 1 | 2 | |
|---|---|---|---|---|---|---|
| 0.25 | 1 | 4 | 4 | 1 | 0.25 |
График будет стремиться к оси по мере увеличения , а вблизи оси значения функции будут очень большими.
2) Отразим график относительно оси абсцисс
Отражение графика относительно оси абсцисс означает замену знака функции на противоположный, т.е. мы меняем знак на отрицательный:
Теперь график будет располагаться ниже оси для всех .
3) Совершим растяжение графика от оси с коэффициентом
Теперь каждый -координат будет умножен на 2, что приведет к растяжению графика вдоль оси . Если для функции при значение , то для новой функции значение будет .
Это означает, что график будет растянут по вертикали, и его значения будут удвоены по сравнению с графиком .