ГДЗ по Алгебре 10 Класс Номер 17.10 Профильный Уровень Мордкович — Подробные Ответы

а) $y = 2|\cos x|$

б) $y=-3\cos \mathrm{\mid }x+\frac{\pi }{6}\mathrm{\mid }$

в) $y = 3\sin|x|$

г) $y = -2\left|\sin\left(x — \frac{\pi}{3}\right)\right|$

а) $y = 2|\cos x|$:

Построим дугу графика $y = \cos x$;

Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;

Достроим график функции (все дуги расположены над осью $Ox$):

б) $y = -3\cos|x + \frac{\pi}{6}| = -3\cos\left(\pm\left(x + \frac{\pi}{6}\right)\right) = -3\cos\left(x + \frac{\pi}{6}\right)$:

Построим дугу графика $y = \cos x$, а затем:

• Переместим ее на $\frac{\pi}{6}$ единиц влево вдоль оси абсцисс;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 3$;

Достроим график функции:

в) $y = 3\sin|x|$:

Построим дугу графика $y = \sin x$, а затем:

• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 3$;

Достроим график функции (симметрично относительно оси $Oy$):

г) $y = -2\left|\sin\left(x — \frac{\pi}{3}\right)\right|$:

Построим дугу графика $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{3}$ единиц вправо вдоль оси абсцисс;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;

Достроим график функции (все дуги расположены под осью $Ox$):

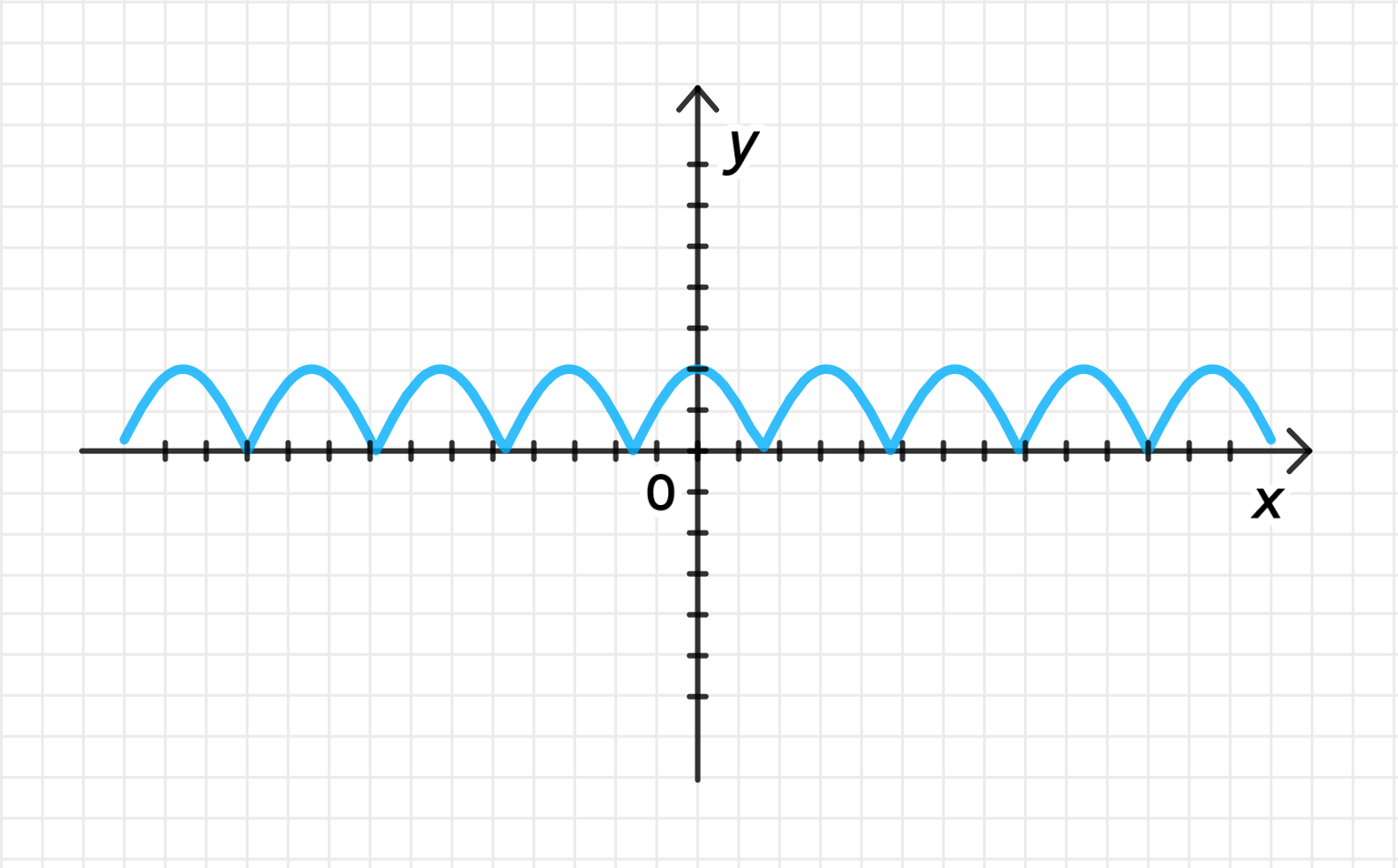
а) $y = 2|\cos x|$:

Построение графика функции $y = \cos x$:

• Функция $y = \cos x$ является косинусом, и ее график представляет собой периодическую кривую с периодом $2\pi$, максимальное значение которой равно 1, а минимальное значение — -1. График имеет вид волны, колеблющейся между 1 и -1 вдоль оси $Oy$, с амплитудой 1.

Основные характеристики графика:

• $y = \cos x$ достигает максимума $1$ в точках $x = 2k\pi$ (где $k$ — целое число).
• $y = \cos x$ достигает минимума $-1$ в точках $x = (2k + 1)\pi$.

Растяжение графика функции от оси $Ox$ с коэффициентом $k = 2$:

• Чтобы растянуть график функции $y = \cos x$ с коэффициентом $k = 2$, нужно увеличить амплитуду графика в 2 раза. Это означает, что для каждого значения $x$, значение функции будет удвоено. То есть теперь:

  $$y = 2 \cos x$$

  Это приведет к тому, что максимальные значения графика будут равны 2, а минимальные — -2, в отличие от исходного графика.

Модуль функции $y = 2|\cos x|$:

• Взятие модуля из функции $\cos x$ означает, что все отрицательные значения на графике становятся положительными. Функция $y = 2|\cos x|$ будет колебаться между 0 и 2 вдоль оси $Oy$, и все дуги графика будут находиться выше оси $Ox$.
• То есть, на графике функции не будет точек, где значение $y$ отрицательно, так как модуль всегда возвращает положительные значения.

Характеристики функции:

• Период графика остается $2\pi$, так как мы не меняем период функции.
• График будет иметь «рёберный» вид, так как фрагменты кривой, где $\cos x$ был отрицательным, будут теперь отражены и расположены выше оси $Ox$.

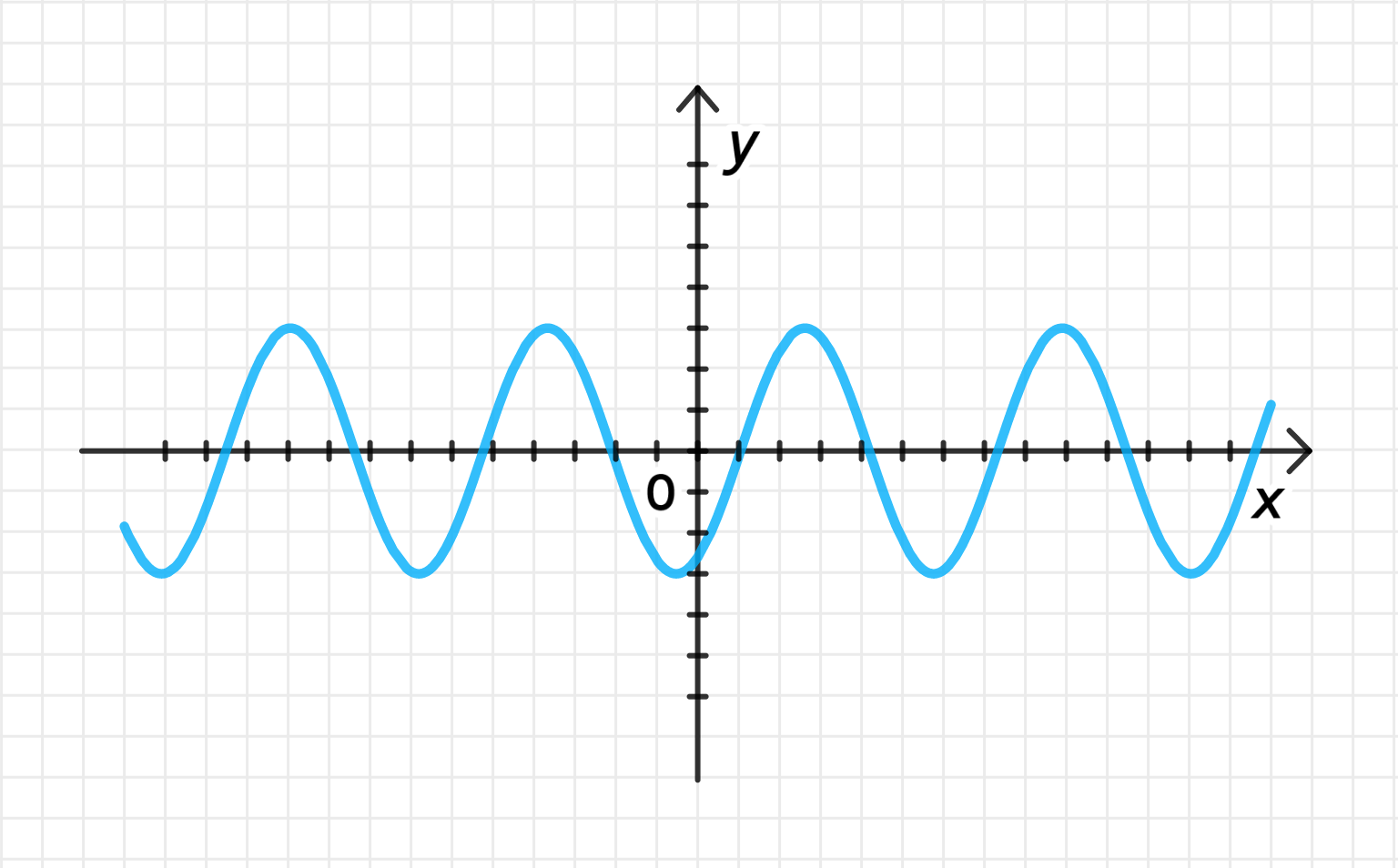
б) $y = -3\cos|x + \frac{\pi}{6}| = -3\cos\left(\pm\left(x + \frac{\pi}{6}\right)\right) = -3\cos\left(x + \frac{\pi}{6}\right)$:

Построение графика функции $y = \cos x$:

• Как и в предыдущем случае, начнем с графика функции $y = \cos x$. Это обычная косинусная волна, как в пункте а, с периодом $2\pi$, амплитудой 1 и максимумом в точках $x = 2k\pi$, минимумом в точках $x = (2k+1)\pi$.

Перемещение графика функции $y = \cos x$ на $\frac{\pi}{6}$ единиц влево вдоль оси абсцисс:

• Для того чтобы переместить график функции $y = \cos x$ на $\frac{\pi}{6}$ единиц влево, мы должны изменить аргумент косинуса следующим образом:

  $$y = \cos\left(x + \frac{\pi}{6}\right)$$

  Это означает, что все точки на графике сдвигаются влево на $\frac{\pi}{6}$ единиц.

Отражение графика относительно оси абсцисс:

• Отражение относительно оси $Ox$ влечет изменение знака функции. Теперь вместо $\cos(x + \frac{\pi}{6})$ мы рассматриваем $-\cos(x + \frac{\pi}{6})$. Это приводит к тому, что график, который раньше был выше оси $Ox$, теперь окажется ниже оси.

Растяжение графика функции от оси $Ox$ с коэффициентом $k = 3$:

• Умножив функцию на 3, мы растягиваем график по вертикали, увеличив амплитуду. Таким образом, все значения функции изменяются на коэффициент 3. Теперь максимальное значение будет равно -3, а минимальное значение будет равно 3 (так как график отражен относительно оси $Ox$).

Достроение графика функции:

• После всех этих преобразований график будет иметь период $2\pi$, отражен относительно оси $Ox$, и колебаться от -3 до 0 (поскольку модуля нет и все значения отрицательные).

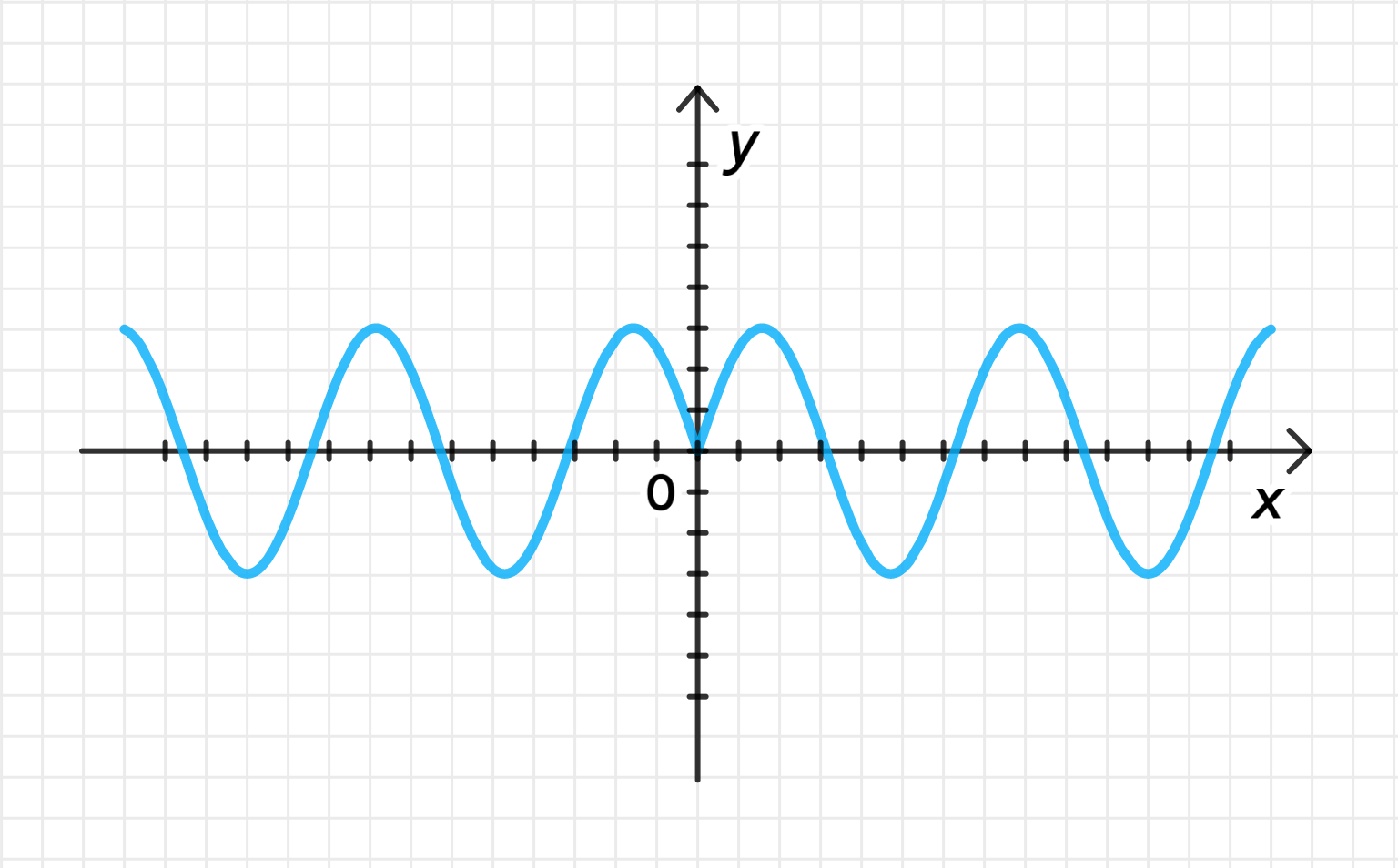
в) $y = 3\sin|x|$:

Построение графика функции $y = \sin x$:

• График функции $y = \sin x$ является синусоидой с периодом $2\pi$, максимумом в точке $x = \frac{\pi}{2}$ и минимумом в точке $x = \frac{3\pi}{2}$. График колеблется между -1 и 1 вдоль оси $Oy$.

Растяжение графика функции от оси $Ox$ с коэффициентом $k = 3$:

• Умножив функцию $y = \sin x$ на 3, мы увеличиваем амплитуду графика в 3 раза. Теперь максимальное значение функции равно 3, а минимальное -3. График будет колебаться между -3 и 3 вдоль оси $Oy$.

Применение модуля к функции $y = 3\sin|x|$:

• Взятие модуля функции $\sin x$ означает, что для всех значений $x$ функция принимает только положительные значения. Таким образом, график функции будет симметричен относительно оси $Oy$, и все отрицательные части синусоиды будут отзеркалены в положительную область.
• График будет колебаться между 0 и 3.

Достроение графика функции:

• Период графика функции останется равным $2\pi$, а сам график будет симметричен относительно оси $Oy$, колеблясь между 0 и 3.

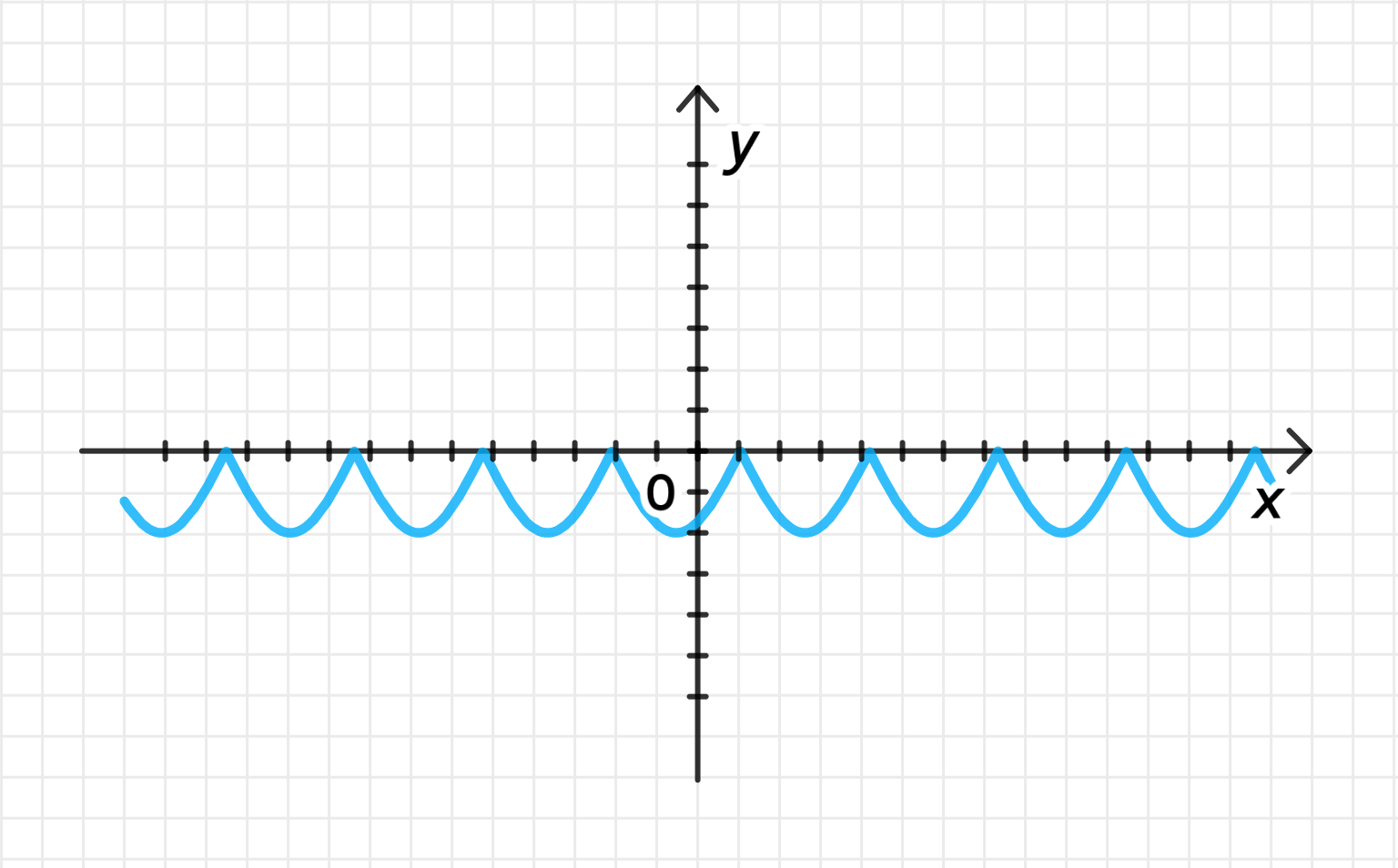
г) $y = -2\left|\sin\left(x — \frac{\pi}{3}\right)\right|$:

Построение графика функции $y = \sin x$:

• Начнем с графика стандартной синусоиды, как в пунктах а и б. Этот график колеблется между -1 и 1, с периодом $2\pi$.

Перемещение графика на $\frac{\pi}{3}$ единиц вправо:

• Для сдвига графика функции $y = \sin x$ на $\frac{\pi}{3}$ единиц вправо, мы изменяем аргумент функции следующим образом:

  $$y = \sin\left(x — \frac{\pi}{3}\right)$$

  Это сдвигает график функции вправо, и все точки на графике сдвигаются на $\frac{\pi}{3}$ единиц.

Отражение графика относительно оси абсцисс:

• После того, как мы отразим график относительно оси $Ox$, у нас получится:

  $$y = -\sin\left(x — \frac{\pi}{3}\right)$$

  Это изменяет знаки всех значений на графике, и теперь вместо того, чтобы график находился выше оси, он окажется ниже.

Растяжение графика по вертикали с коэффициентом 2:

• Умножив функцию на 2, мы растягиваем график по вертикали в 2 раза. Теперь максимальное значение функции будет равно -2, а минимальное значение -1, и график будет колебаться между 0 и -2.

Применение модуля:

• Взятие модуля из синусоиды сдвигает все значения в положительную область. Таким образом, после применения модуля, график функции будет колебаться между 0 и 2, а его форма будет «рёберной».

Достроение графика функции:

• График будет периодически колебаться между 0 и 2, отраженный относительно оси $Ox$.