ГДЗ по Алгебре 10 Класс Номер 17.14 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а)

$$y=\{\begin{array}{ll}3\sin x,& \text{если }x<\frac{\pi }{2}\\ 3x^3,& \text{если }x\ge \frac{\pi }{2}\end{array}$$

б)

$$y=\{\begin{array}{ll}-2\cos x,& \text{если }x<0\\ \frac{1}{2}{x}^4,& \text{если }x\ge 0\end{array}$$

В данной задаче $n$ — целое неотрицательное число;

а)

$$y=\{\begin{array}{ll}3\sin x,& \text{если }x<\frac{\pi }{2};\\ 3x^3,& \text{если }x\ge \frac{\pi }{2}\end{array}$$

$y=3\sin x$ — уравнение синусоиды:

$$y\left(\frac{\pi }{2}\right)=3\sin \frac{\pi }{2}=3\cdot 1=3;$$

$y=3x^3$ — уравнение кубической параболы:

$$x_0=0,y_0=0;$$$$\overline{)\begin{array}{ccc}x& \frac{\pi }{2}& \frac{2\pi }{3}\\ y& \approx 11,6& \approx 27,5\end{array}}$$

Графики функций:

Свойства функции:

• Область определения: $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$;
• Множество значений: $E(f)=[-3;+\mathrm{\infty })$;
• Возрастает на $[-\frac{\pi }{2}-2\pi n;\frac{\pi }{2}-2\pi n]\cup [\frac{\pi }{2};+\mathrm{\infty })$;
• Убывает на $[-\frac{3\pi }{2}-2\pi n;-\frac{\pi }{2}-2\pi n]$;
• $f(x)>0$ на $(-2\pi -2\pi n;-\pi -2\pi n)\cup (0;+\mathrm{\infty })$;
• $f(x)<0$ на $(-\pi -2\pi n;-2\pi n)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической;

б)

$$y=\{\begin{array}{ll}-2\cos x,& \text{если }x<0;\\ \frac{1}{2}{x}^4,& \text{если }x\ge 0\end{array}$$

$y=-2\cos x$ — уравнение косинусоиды:

$$y(0)=-2\cos 0=-2\cdot 1=-2;$$

$y=\frac{1}{2}{x}^4$ — уравнение параболы:

$$x_0=0,y_0=0;$$$$\overline{)\begin{array}{ccccc}x& 0& 1& 1.5& 2\\ y& 0& 0.5& \approx 2.5& 8\end{array}}$$

Графики функций:

Свойства функции:

• Область определения: $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$;
• Множество значений: $E(f)=[-2;+\mathrm{\infty })$;
• Возрастает на $[-2\pi -2\pi n;-\pi -2\pi n]\cup [0;+\mathrm{\infty })$;
• Убывает на $[-\pi -2\pi n;-2\pi n]$;
• $f(x)>0$ на $(-\frac{3\pi }{2}-2\pi n;-\frac{\pi }{2}-2\pi n)\cup (0;+\mathrm{\infty })$;
• $f(x)<0$ на $(-\frac{5\pi }{2}-2\pi n;-\frac{3\pi }{2}-2\pi n)\cup (-\frac{\pi }{2};0)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической

В данной задаче $n$ — целое неотрицательное число;

а)

$$y=\{\begin{array}{ll}3\sin x,& \text{если }x<\frac{\pi }{2};\\ 3x^3,& \text{если }x\ge \frac{\pi }{2}\end{array}$$

1) $y=3\sin x$ — уравнение синусоиды:

Мы начинаем с анализа функции $y=3\sin x$, которая задана на интервале $(-\mathrm{\infty };\frac{\pi }{2})$.

• В точке $x=\frac{\pi }{2}$ вычислим значение функции:$$y\left(\frac{\pi }{2}\right)=3\sin \frac{\pi }{2}=3\cdot 1=3$$

  Таким образом, при $x=\frac{\pi }{2}$ функция достигает значения 3, что также является точкой перехода на другую ветвь функции.

2) $y=3x^3$ — уравнение кубической параболы:

Для функции $y=3x^3$, которая определена на интервале $[\frac{\pi }{2};+\mathrm{\infty })$, мы также анализируем её значения в нескольких точках:

• В точке $x=0$ (граница перехода между ветвями):$$y_0=3\cdot 0^3=0$$

  То есть, при $x=0$ график функции проходит через начало координат.

• Для вычисления значений функции в других точках подставим конкретные значения $x$:
  • Для $x=\frac{\pi }{2}$:

  $$y\left(\frac{\pi }{2}\right)=3{\left(\frac{\pi }{2}\right)}^3=3\cdot \frac{{\pi }^3}{8}\approx 11,6$$

  • Для $x=\frac{2\pi }{3}$:

  $$y\left(\frac{2\pi }{3}\right)=3{\left(\frac{2\pi }{3}\right)}^3=3\cdot \frac{8{\pi }^3}{27}\approx 27,5$$

Итак, значения функции на интервале $[\frac{\pi }{2};+\mathrm{\infty })$ в этих точках будут $y\approx 11,6$ при $x=\frac{\pi }{2}$ и $y\approx 27,5$ при $x=\frac{2\pi }{3}$.

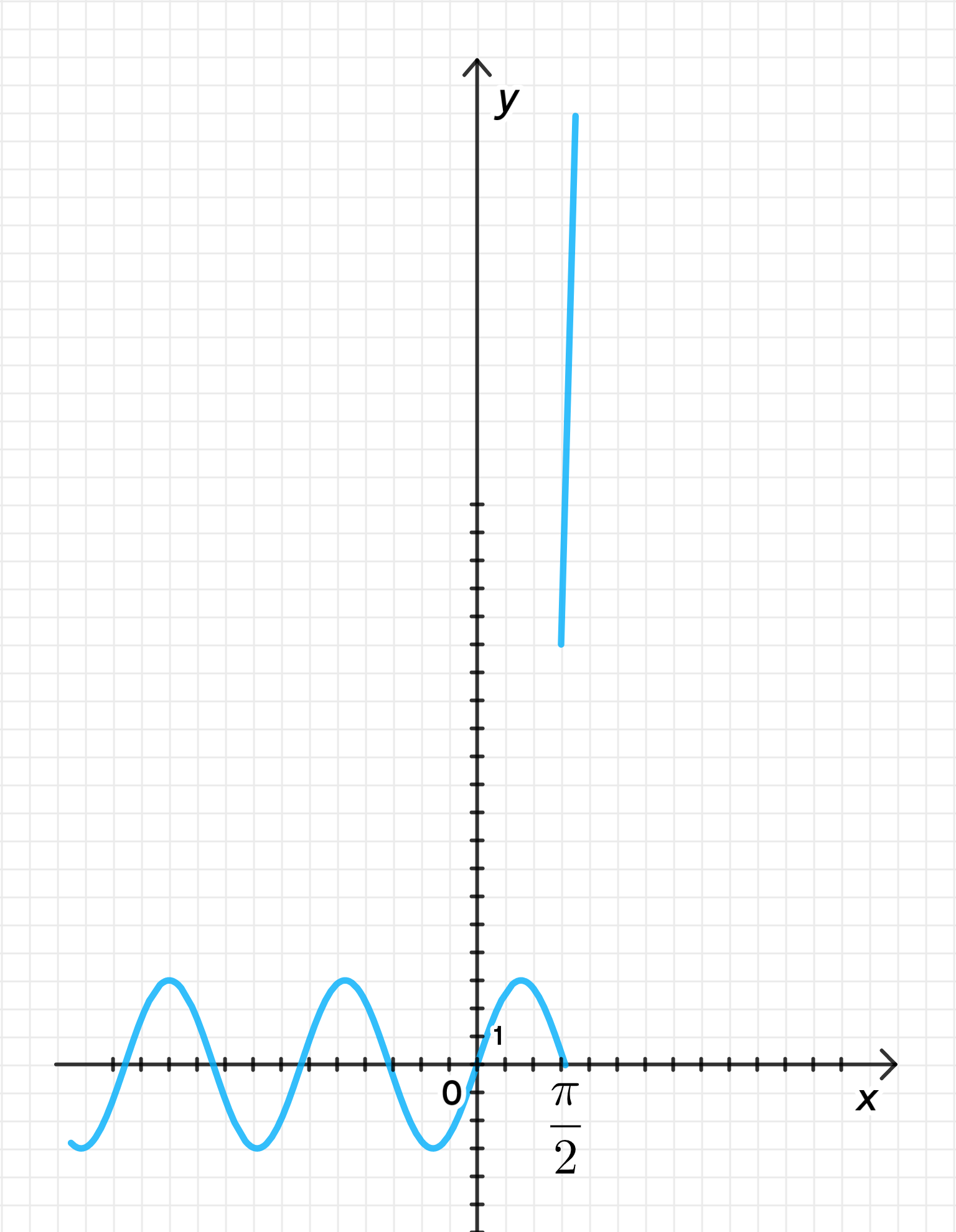
3) Графики функций:

График функции состоит из двух частей:

• Для $x<\frac{\pi }{2}$ график представляет собой синусоиду с амплитудой 3.
• Для $x\ge \frac{\pi }{2}$ график представляет собой кубическую параболу, которая резко возрастает.

Таким образом, функции переходят плавно от синусоиды к кубической параболе в точке $x=\frac{\pi }{2}$, где значения обеих функций совпадают, что подтверждает непрерывность функции.

4) Свойства функции:

Теперь анализируем свойства функции:

• Область определения: поскольку обе функции $3\sin x$ и $3x^3$ определены на всей числовой прямой, то область определения функции $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$.
• Множество значений:
  • Для $y=3\sin x$ на интервале $(-\mathrm{\infty };\frac{\pi }{2})$ максимальное значение синусоиды равно 3, а минимальное — -3.
  • Для $y=3x^3$ на интервале $[\frac{\pi }{2};+\mathrm{\infty })$ функция стремится к бесконечности, а минимальное значение при $x=0$ равно 0.

  Таким образом, общее множество значений функции: $E(f)=[-3;+\mathrm{\infty })$.

• Возрастание и убывание:
  • Для функции $3\sin x$ на интервале $(-\mathrm{\infty };\frac{\pi }{2})$ синусоида возрастает до точки $x=\frac{\pi }{2}$, где она достигает максимума 3.
  • Для функции $3x^3$ на интервале $[\frac{\pi }{2};+\mathrm{\infty })$ она монотонно возрастает, так как кубическая функция возрастает на всем своём определении.

  Таким образом, функция возрастает на интервалах $[-\frac{\pi }{2}-2\pi n;\frac{\pi }{2}-2\pi n]\cup [\frac{\pi }{2};+\mathrm{\infty })$.

  Функция убывает на интервале $[-\frac{3\pi }{2}-2\pi n;-\frac{\pi }{2}-2\pi n]$.

• Знаки функции:
  • $f(x)>0$ на $(-2\pi -2\pi n;-\pi -2\pi n)\cup (0;+\mathrm{\infty })$,
  • $f(x)<0$ на $(-\pi -2\pi n;-2\pi n)$.
• Четность и нечетность: Функция не является ни четной, ни нечетной, так как на разных интервалах функции $3\sin x$ и $3x^3$ ведут себя по-разному.
• Периодичность: Функция не является периодической, так как синусоида и кубическая функция имеют разные характеры поведения, и периодичности как таковой нет.

б)

$$y=\{\begin{array}{ll}-2\cos x,& \text{если }x<0;\\ \frac{1}{2}{x}^4,& \text{если }x\ge 0\end{array}$$

1) $y=-2\cos x$ — уравнение косинусоиды:

Функция $y=-2\cos x$ определена на интервале $(-\mathrm{\infty };0)$. Рассмотрим значение функции в точке $x=0$:

$$y(0)=-2\cos 0=-2\cdot 1=-2;$$

То есть, при $x=0$ функция принимает значение $-2$.

2) $y=\frac{1}{2}{x}^4$ — уравнение параболы:

Для функции $y=\frac{1}{2}{x}^4$, которая определена на интервале $[0;+\mathrm{\infty })$, рассмотрим её значения в нескольких точках:

• В точке $x=0$:$$y_0=\frac{1}{2}\cdot 0^4=0;$$
• В точке $x=1$:$$y(1)=\frac{1}{2}\cdot 1^4=0.5;$$
• В точке $x=1.5$:$$y(1.5)=\frac{1}{2}\cdot {1.5}^4\approx 2.5;$$
• В точке $x=2$:$$y(2)=\frac{1}{2}\cdot 2^4=8;$$

Таким образом, значения функции на интервале $[0;+\mathrm{\infty })$ будут $y=0.5$ при $x=1$, $y\approx 2.5$ при $x=1.5$, и $y=8$ при $x=2$.

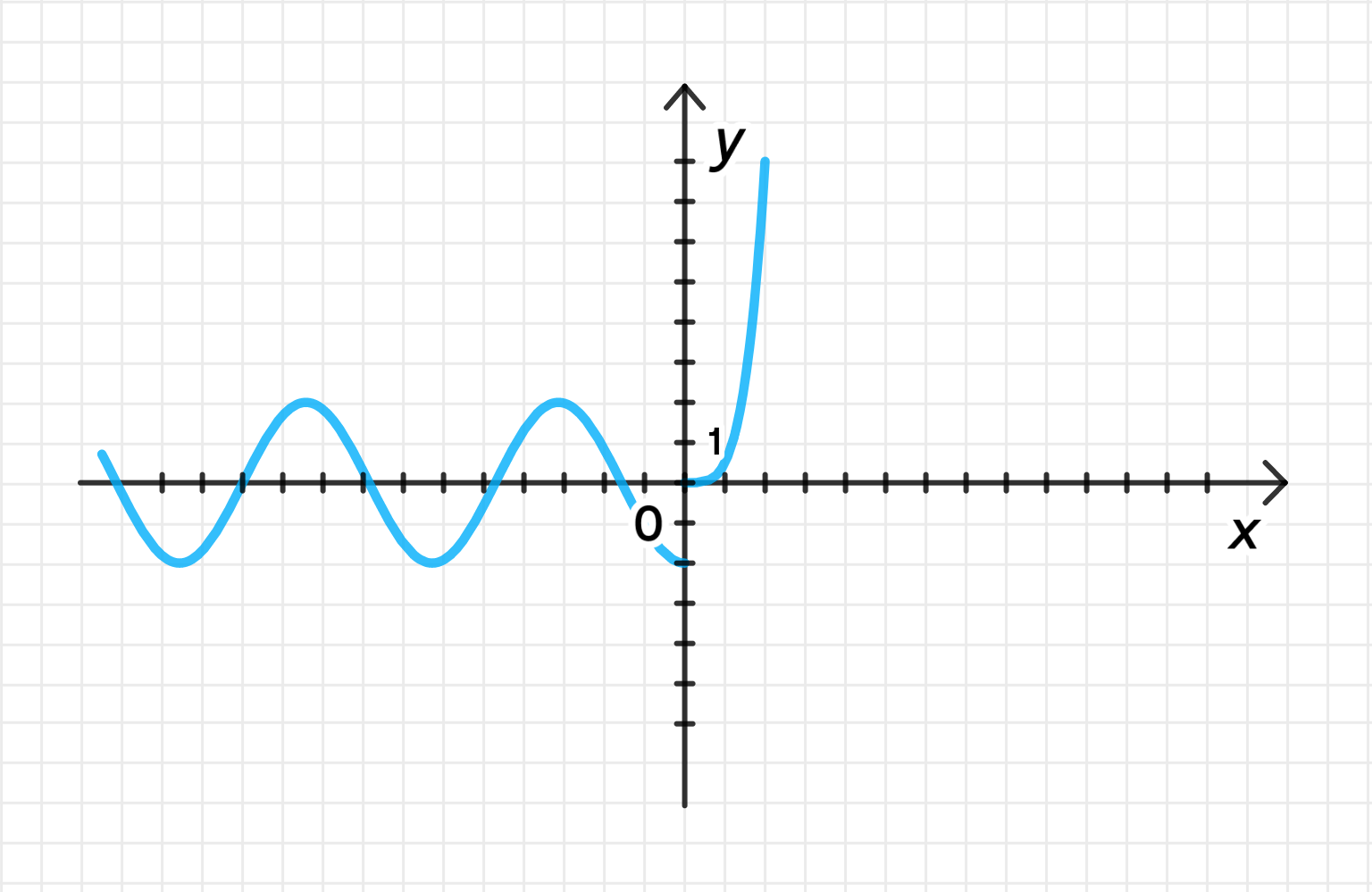
3) Графики функций:

График функции состоит из двух частей:

• Для $x<0$ график представляет собой косинусоиду, умноженную на -2.
• Для $x\ge 0$ график представляет собой параболу $y=\frac{1}{2}{x}^4$, которая монотонно возрастает.

4) Свойства функции:

Теперь анализируем свойства функции:

• Область определения: функция определена на всей числовой прямой, так как и $\cos x$, и $x^4$ определены для всех значений $x$. Область определения функции: $D(f)=(-\mathrm{\infty };+\mathrm{\infty })$.
• Множество значений:
  • Для $y=-2\cos x$ на интервале $(-\mathrm{\infty };0)$ максимальное значение функции равно 2, а минимальное — -2.
  • Для $y=\frac{1}{2}{x}^4$ на интервале $[0;+\mathrm{\infty })$ функция возрастает от 0 до $+\mathrm{\infty }$.

  Таким образом, общее множество значений функции: $E(f)=[-2;+\mathrm{\infty })$.

• Возрастание и убывание:
  • Для функции $-2\cos x$ на интервале $(-\mathrm{\infty };0)$ косинусоида убывает, так как умножена на отрицательное число.
  • Для функции $\frac{1}{2}{x}^4$ на интервале $[0;+\mathrm{\infty })$ парабола монотонно возрастает.

  Функция возрастает на интервалах $[-2\pi -2\pi n;-\pi -2\pi n]\cup [0;+\mathrm{\infty })$.

  Функция убывает на интервале $[-\pi -2\pi n;-2\pi n]$.

• Знаки функции:
  • $f(x)>0$ на $(-\frac{3\pi }{2}-2\pi n;-\frac{\pi }{2}-2\pi n)\cup (0;+\mathrm{\infty })$,
  • $f(x)<0$ на $(-\frac{5\pi }{2}-2\pi n;-\frac{3\pi }{2}-2\pi n)\cup (-\frac{\pi }{2};0)$.
• Четность и нечетность: Функция не является ни четной, ни нечетной, так как на разных интервалах функции ведут себя по-разному.
• Периодичность: Функция не является периодической, так как косинусоиды и полиномиальные функции имеют разные характеры поведения и не могут быть объединены в периодическую функцию.