ГДЗ по Алгебре 10 Класс Номер 17.15 Профильный Уровень Мордкович — Подробные Ответы

Решите уравнение:

а) $2 \sin x — 1 = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9};$

б) $2\cos x=\frac{9x^2}{{\pi }^2}$

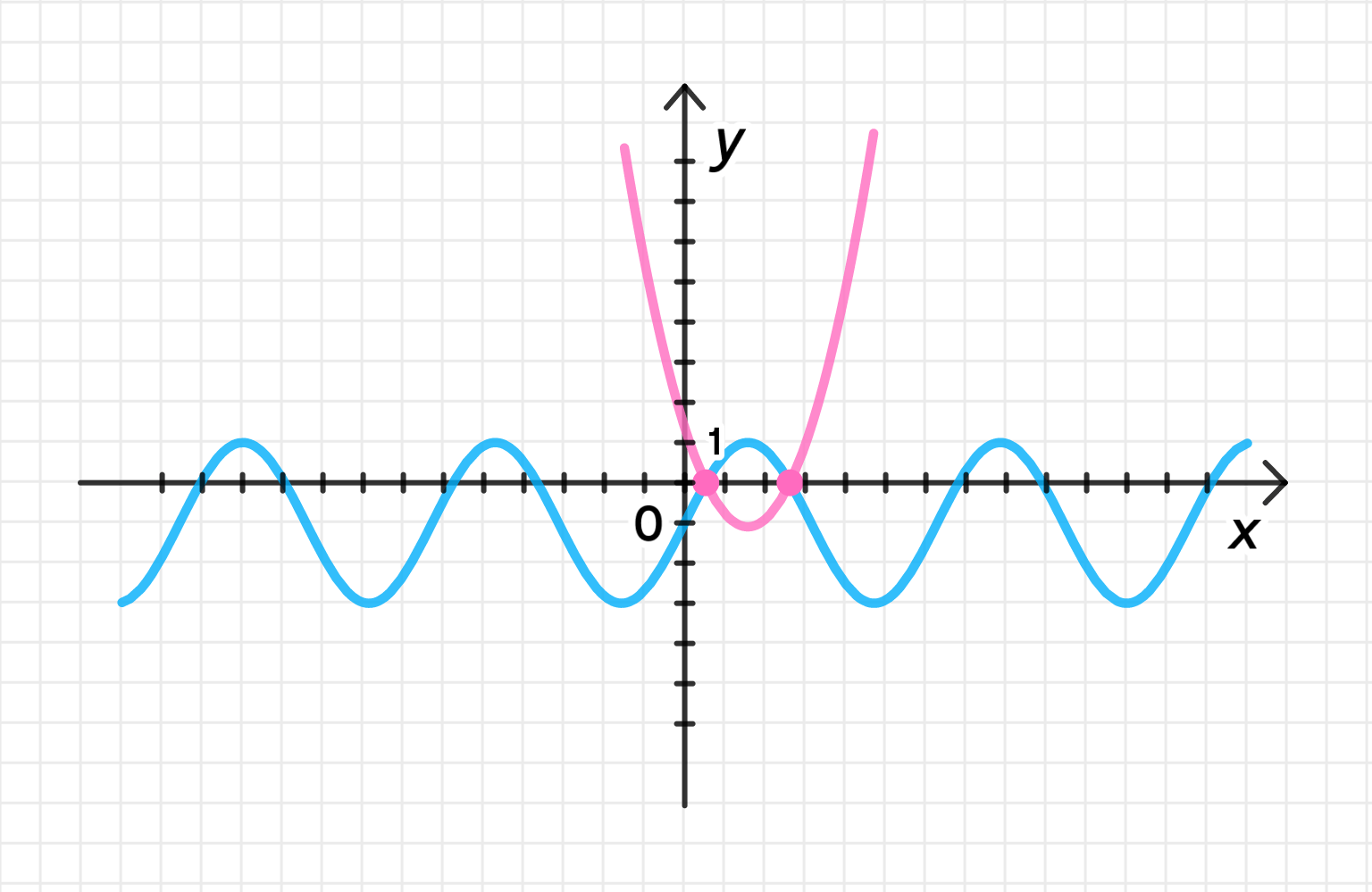
а) $2 \sin x — 1 = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9};$

$y = 2 \sin x — 1$ — уравнение синусоиды;

$y = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9}$ — уравнение параболы:

$x_0 = \frac{\pi}{2}, \; y_0 = -\frac{\pi^2}{9} \approx -1;$

Графики функций:

Ответ: $x_1 = \frac{\pi}{6}, \; x_2 = \frac{5\pi}{6}.$

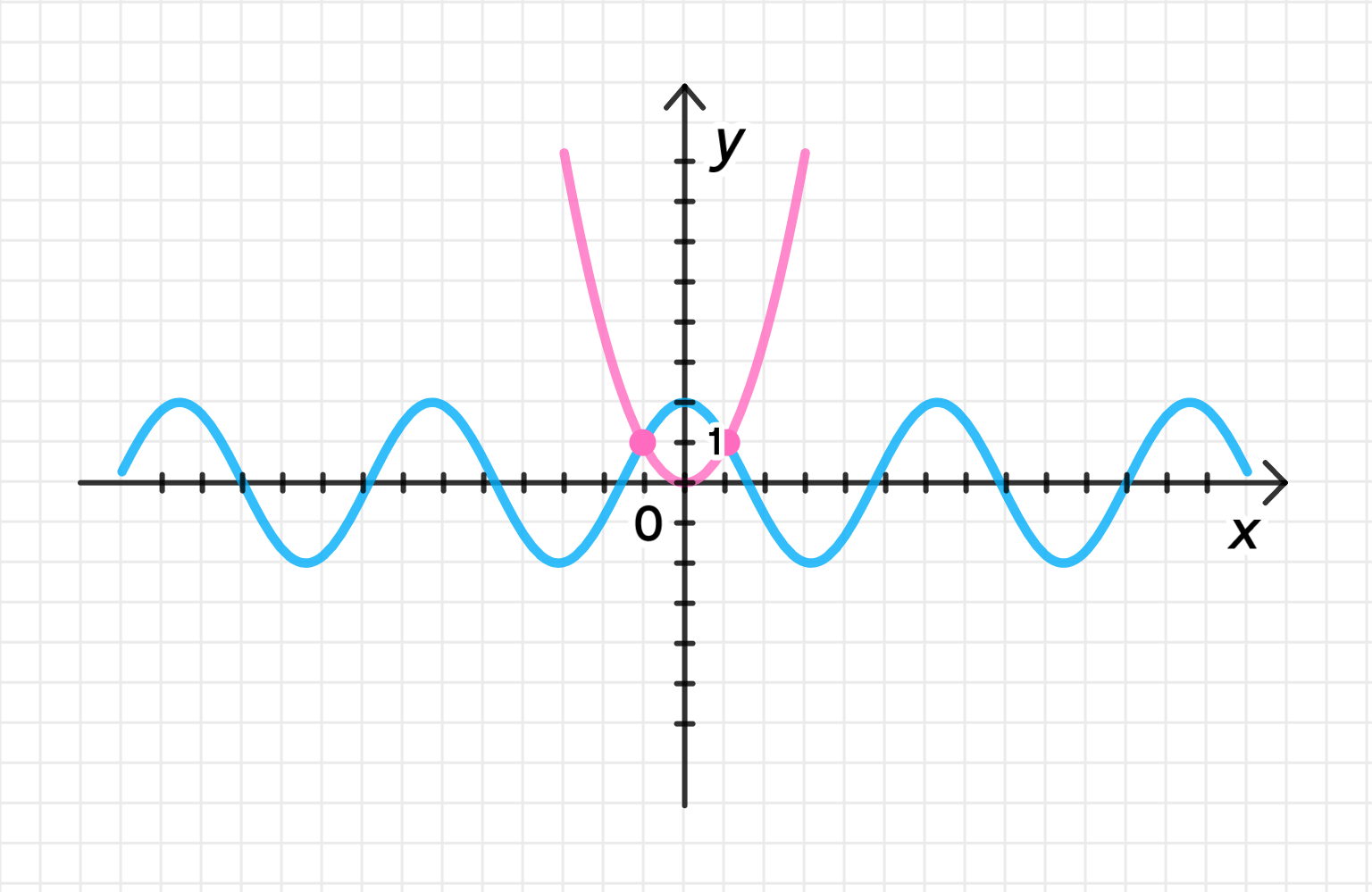
б) $2 \cos x = \frac{9x^2}{\pi^2};$

$y = 2 \cos x$ — уравнение синусоиды;

$y = \frac{9x^2}{\pi^2}$ — уравнение параболы:

$x_0 = 0, \; y_0 = 0;$

Графики функций:

Ответ: $x = \pm \frac{\pi}{3}.$

а) $2 \sin x — 1 = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9}$

1) Уравнение синусоиды: $y = 2 \sin x — 1$

• Эта функция представляет собой синусоиду с амплитудой 2 и сдвигом вниз на 1. Синусоида будет колебаться вокруг оси $y = -1$ с амплитудой 2.
  • Максимальное значение функции $y = 2 \sin x — 1$:

    $$\text{Максимум} = 2 \cdot 1 — 1 = 1$$

    Это происходит, когда $\sin x = 1$, что происходит при $x = \frac{\pi}{2} + 2k\pi$, где $k$ — целое число.

  • Минимальное значение функции:

    $$\text{Минимум} = 2 \cdot (-1) — 1 = -3$$

    Это происходит, когда $\sin x = -1$, что происходит при $x = \frac{3\pi}{2} + 2k\pi$, где $k$ — целое число.

• Таким образом, функция $y = 2 \sin x — 1$ колеблется между -3 и 1.

2) Уравнение параболы: $y = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9}$

• Это уравнение описывает параболу с вершиной в точке $x_0 = \frac{\pi}{2}$ и значением $y_0 = -\frac{\pi^2}{9} \approx -1$, так как $\left( \frac{\pi}{2} — \frac{\pi}{2} \right)^2 = 0$.
• Чтобы найти другие значения функции на различных точках, подставим несколько значений $x$ в уравнение.
  • Для $x = \frac{\pi}{6}$:

    $$y = \left( \frac{\pi}{6} — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9} = \left( -\frac{\pi}{3} \right)^2 — \frac{\pi^2}{9} = \frac{\pi^2}{9} — \frac{\pi^2}{9} = 0$$

  • Для $x = \frac{\pi}{2}$:

    $$y = \left( \frac{\pi}{2} — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9} = 0^2 — \frac{\pi^2}{9} = -\frac{\pi^2}{9} \approx -1$$

  • Для $x = \frac{5\pi}{6}$:

    $$y = \left( \frac{5\pi}{6} — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9} = \left( \frac{\pi}{3} \right)^2 — \frac{\pi^2}{9} = \frac{\pi^2}{9} — \frac{\pi^2}{9} = 0$$

Таким образом, значения функции в этих точках:

• $x = \frac{\pi}{6}$, $y = 0$
• $x = \frac{\pi}{2}$, $y \approx -1$
• $x = \frac{5\pi}{6}$, $y = 0$

3) Графики функций:

• График синусоиды $y = 2 \sin x — 1$ — это стандартная синусоида, сдвинутая вниз на 1 и растянутая по амплитуде на 2.
• График параболы $y = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9}$ — это парабола, открывающаяся вверх с вершиной в точке $\left( \frac{\pi}{2}, -\frac{\pi^2}{9} \right)$.

Графики этих двух функций пересекаются в точках, где $y = 2 \sin x — 1 = \left( x — \frac{\pi}{2} \right)^2 — \frac{\pi^2}{9}$. Из анализа полученных значений:

• $x_1 = \frac{\pi}{6}$
• $x_2 = \frac{5\pi}{6}$

Ответ: $x_1 = \frac{\pi}{6}, \; x_2 = \frac{5\pi}{6}$.

б) $2 \cos x = \frac{9x^2}{\pi^2}$

1) Уравнение синусоиды: $y = 2 \cos x$

• Это уравнение описывает косинусоиду с амплитудой 2 и сдвигом вдоль оси $y$, так что максимальное значение функции $y = 2 \cos x$ равно 2, а минимальное — -2.
  • Максимальное значение:

    $$\text{Максимум} = 2 \cdot 1 = 2$$

    Это происходит, когда $\cos x = 1$, что происходит при $x = 2k\pi$, где $k$ — целое число.

  • Минимальное значение:

    $$\text{Минимум} = 2 \cdot (-1) = -2$$

    Это происходит, когда $\cos x = -1$, что происходит при $x = \pi + 2k\pi$, где $k$ — целое число.

2) Уравнение параболы: $y = \frac{9x^2}{\pi^2}$

• Это уравнение описывает параболу, открывающуюся вверх с вершиной в точке $(0, 0)$, так как при $x = 0$, $y = 0$.
• Для поиска точек пересечения этих функций подставим несколько значений $x$.
  • Для $x = -\frac{\pi}{3}$:

    $$y = \frac{9 \left( -\frac{\pi}{3} \right)^2}{\pi^2} = \frac{9 \cdot \frac{\pi^2}{9}}{\pi^2} = 1$$

  • Для $x = 0$:

    $$y = \frac{9 \cdot 0^2}{\pi^2} = 0$$

  • Для $x = \frac{\pi}{3}$:

    $$y = \frac{9 \left( \frac{\pi}{3} \right)^2}{\pi^2} = \frac{9 \cdot \frac{\pi^2}{9}}{\pi^2} = 1$$

Значения функции на интервале:

• $x = -\frac{\pi}{3}$, $y = 1$
• $x = 0$, $y = 0$
• $x = \frac{\pi}{3}$, $y = 1$

3) Графики функций:

• График косинусоиды $y = 2 \cos x$ — это стандартная косинусоида с амплитудой 2, колеблющаяся между -2 и 2.
• График параболы $y = \frac{9x^2}{\pi^2}$ — это парабола, которая начинается с вершины в $(0, 0)$ и монотонно возрастает.

Точки пересечения этих функций:

• $x = -\frac{\pi}{3}$
• $x = \frac{\pi}{3}$

Ответ: $x = \pm \frac{\pi}{3}$.$x = \pm \frac{\pi}{3}.$