Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 17.16 Профильный Уровень Мордкович — Подробные Ответы
Решите неравенство:
а) ;
б)
а) ;
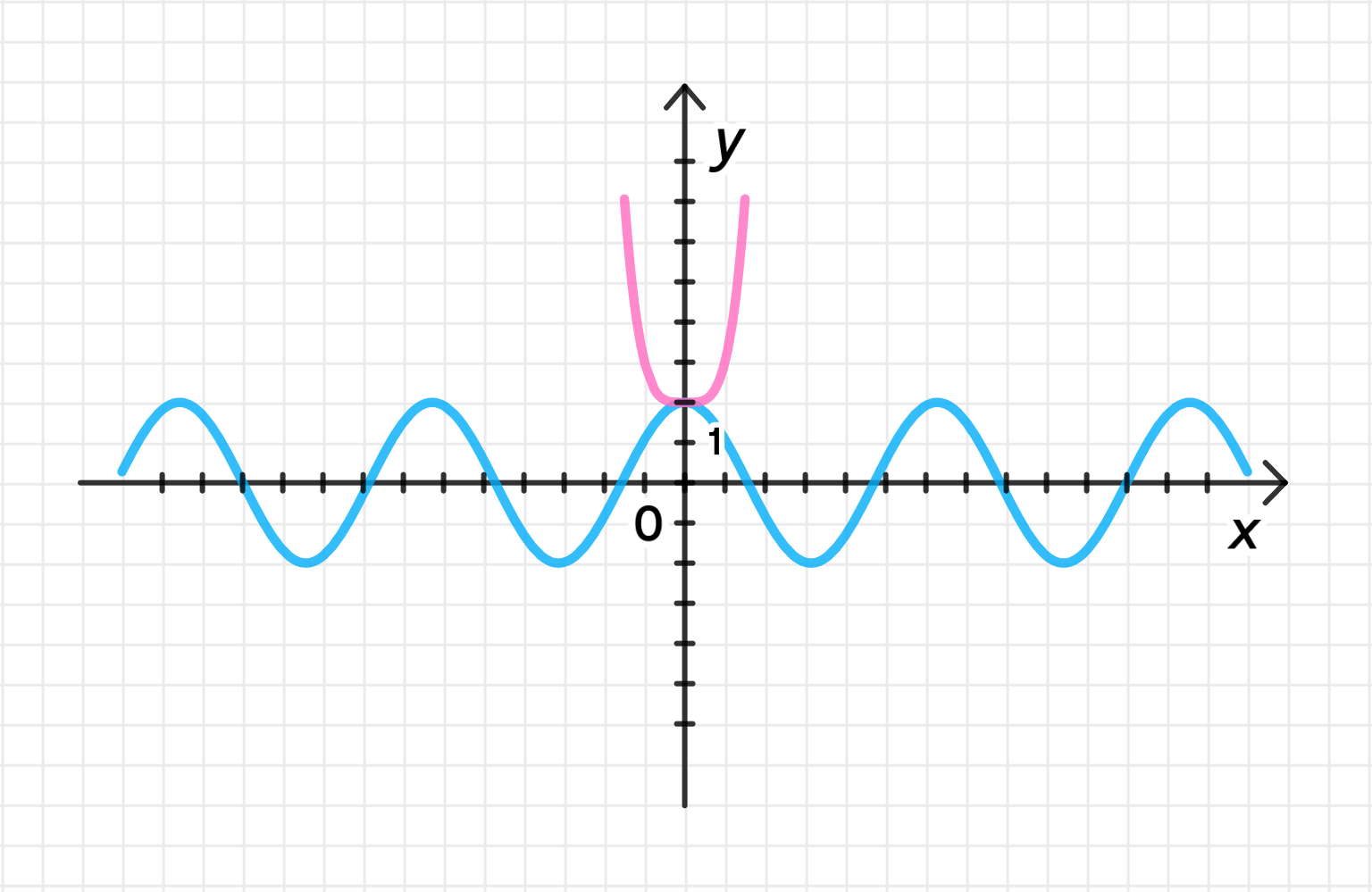
— уравнение синусоиды;
— уравнение параболы:
;
Графики функций:
Ответ: .
б) ;
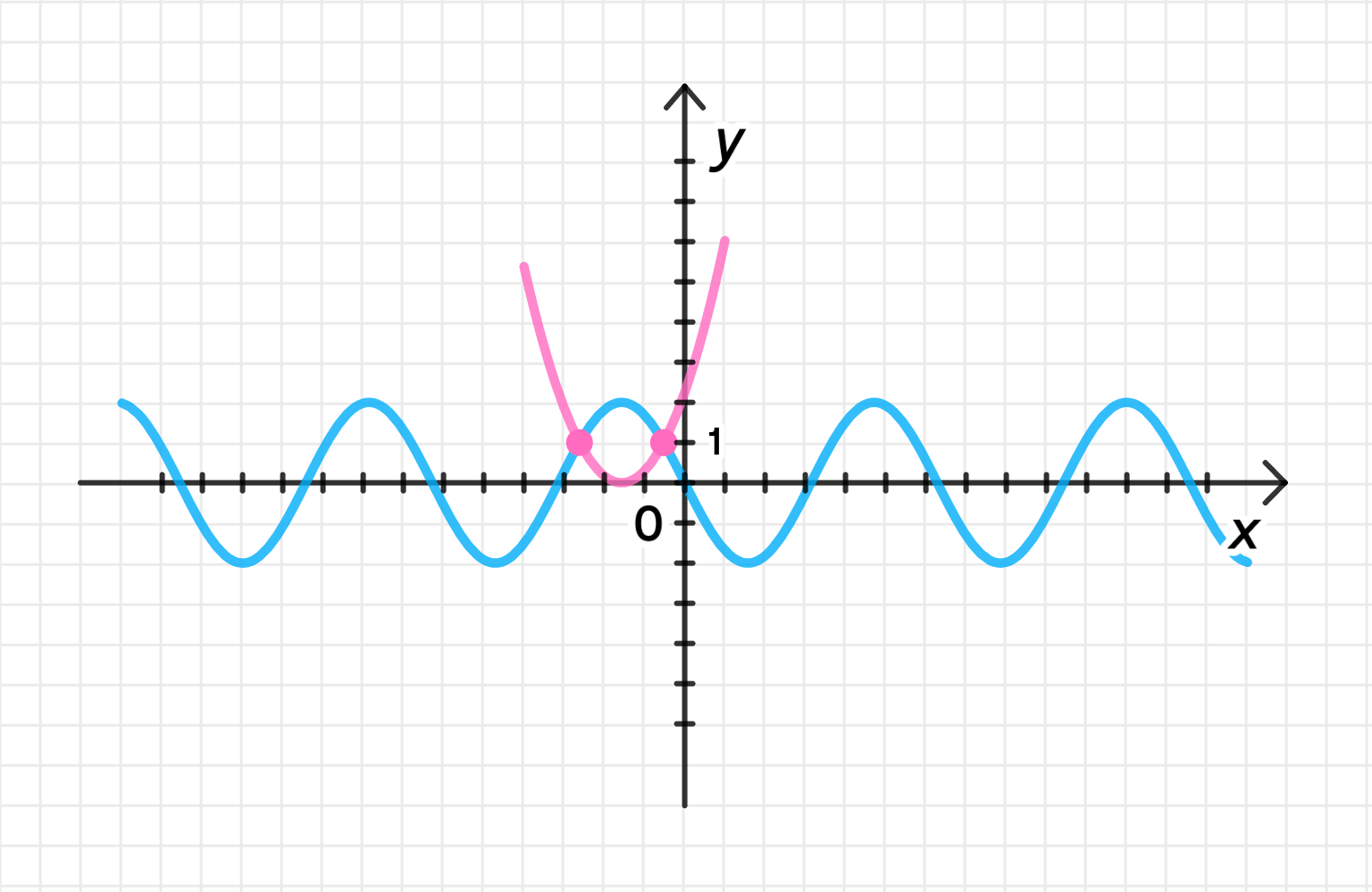
— уравнение синусоиды;
— уравнение параболы:
;
Графики функций:
Ответ: .
а)
1) Уравнение синусоиды
Это стандартное уравнение для функции косинуса с амплитудой 2. Основные моменты:
- Амплитуда функции равна 2, то есть максимум функции равен 2, а минимум — -2.
- Функция периодична с периодом , но при умножении на 2 амплитуда меняется, но период остается тот же. То есть функция будет периодически изменяться между значениями 2 и -2, с периодом .
2) Уравнение параболы
Это уравнение параболы, открывающейся вверх. Важные моменты:
- Вершина параболы находится в точке , где , так как при значение .
- Для любых других значений , функция будет возрастать. Например, при мы получаем , а при аналогично .
- Парабола симметрична относительно оси -ошибки, то есть для всех значение будет одинаковым для и .
3) Графики функций
Решим неравенство:
Неравенство нужно решить для . Точно это сделать можно только численно или графически, но можно оценить, что в точке обе функции равны 2, и затем необходимо исследовать поведение этих функций для других значений .
- Для :
Обе функции равны 2, то есть на неравенство не выполняется.
- Для :
Здесь , то есть неравенство выполняется.
- Для :
Так как , неравенство выполняется.
- Для :
Неравенство выполняется, так как .
Следовательно, неравенство выполняется для всех . В точке оно не выполняется, потому что обе функции дают одинаковое значение 2. Таким образом, ответ: .
б)
1) Уравнение синусоиды
Это также стандартная синусоидальная функция, но с определенными модификациями:
- Амплитуда функции равна 2, то есть функция будет изменяться от -2 до 2.
- Функция синуса периодична, с периодом . Однако при умножении на -2 амплитуда не изменяется, только функция меняет знак. То есть она будет колебаться между -2 и 2.
- Максимум функции равен 2, а минимум — -2.
2) Уравнение параболы
Это парабола, открывающаяся вверх. Важные моменты:
- Вершина параболы находится в точке , где . То есть для значение , а для других значений функция возрастает.
- Например, при мы получаем:
- Парабола симметрична относительно точки .
3) Графики функций
Теперь решим неравенство:
Для :
Неравенство выполняется, так как .
Для :
Здесь , неравенство также выполняется.
Для :
Здесь , то есть неравенство не выполняется.
Ответ: Неравенство выполняется при , так как на этих отрезках левая часть больше правой.