ГДЗ по Алгебре 10 Класс Номер 17.17 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\frac{3{\sin }^{3}x}{1-{\cos }^{2}x}$

б) $y=\frac{{\cos }^{3}x}{2{\sin }^{2}x-2}$$$$$

а) $y = \frac{3 \sin^3 x}{1 — \cos^2 x} = \frac{3 \sin^3 x}{\sin^2 x} = 3 \sin x$;

Выражение имеет смысл при:

• $\sin x \neq 0$;
• $x \neq \pi n$;

График функции:

б) $y = \frac{\cos^3 x}{2 \sin^2 x — 2} = \frac{\cos^3 x}{-2(1 — \sin^2 x)} = -\frac{\cos^3 x}{-2 \cos^2 x} = -\frac{1}{2} \cos x$;

Выражение имеет смысл при:

• $\cos x \neq 0$;
• $x \neq \pm \frac{\pi}{2} + 2\pi n$;

График функции:

а) $y = \frac{3 \sin^3 x}{1 — \cos^2 x} = \frac{3 \sin^3 x}{\sin^2 x} = 3 \sin x$

1) Преобразование выражения

Мы начнем с преобразования исходного выражения.

Исходное выражение:

$$y = \frac{3 \sin^3 x}{1 — \cos^2 x}$$

Заметив, что:

$$1 — \cos^2 x = \sin^2 x \quad \text{(из основной тригонометрической тождества)}.$$

Мы можем подставить это в исходное выражение:

$$y = \frac{3 \sin^3 x}{\sin^2 x}.$$

Теперь сокращаем $\sin^2 x$ в числителе и знаменателе (при условии, что $\sin x \neq 0$):

$$y = 3 \sin x.$$

Это и есть окончательное преобразованное выражение.

2) Условия, при которых выражение имеет смысл

Давайте рассмотрим, при каких значениях $x$ выражение имеет смысл.

• В исходной функции у нас есть дробь $\frac{3 \sin^3 x}{1 — \cos^2 x}$. Для того, чтобы выражение было определено, знаменатель не должен быть равен нулю:

  $$1 — \cos^2 x = \sin^2 x \neq 0.$$

  Это означает, что $\sin x \neq 0$, а значит, $x \neq n\pi$, где $n$ — целое число. Таким образом, $x$ не может быть кратным $\pi$, так как в этих точках $\sin x = 0$.

• Также важно отметить, что при $\sin x = 0$, выражение становится неопределенным, так как деление на ноль невозможно.

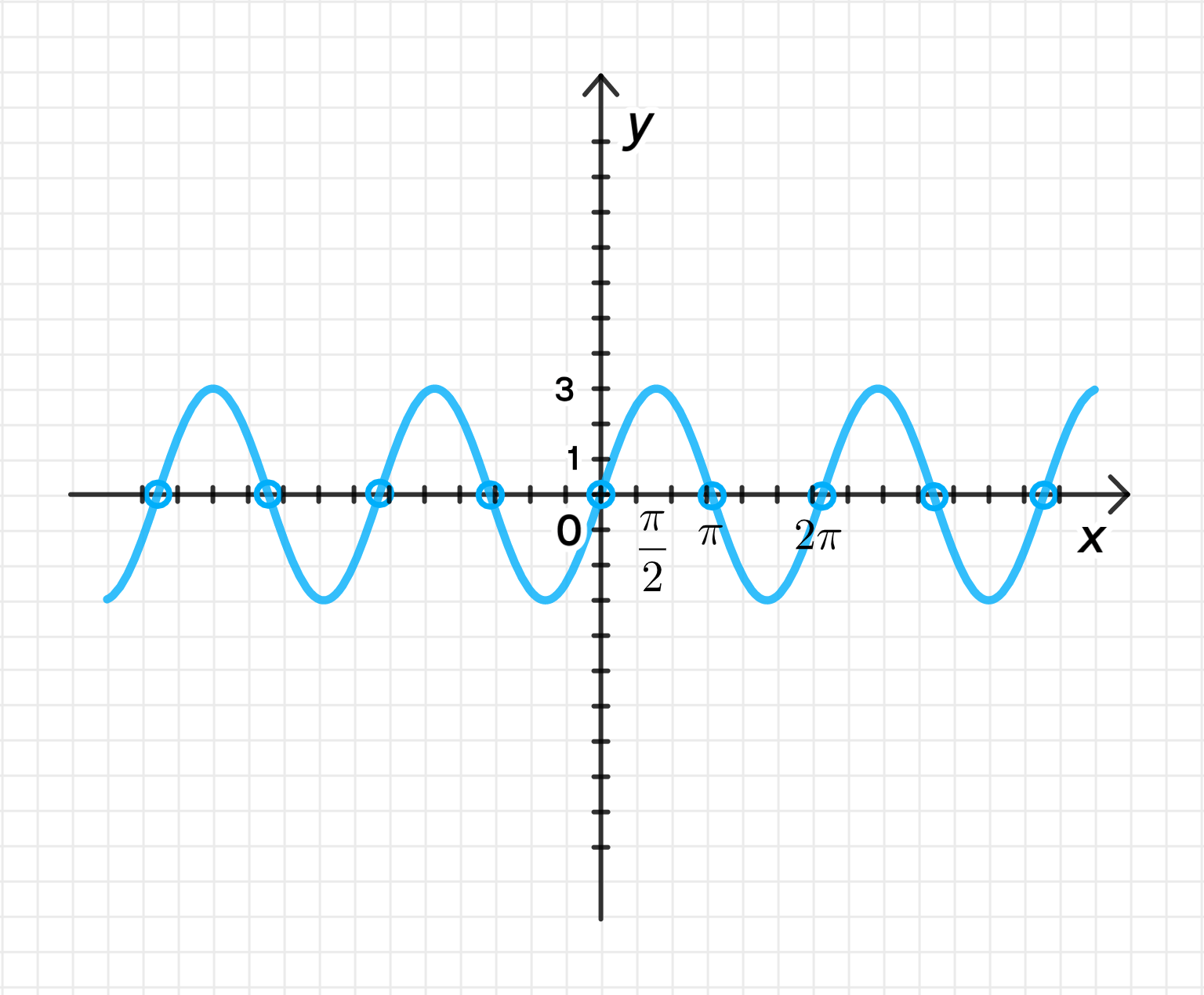
3) График функции

Функция $y = 3 \sin x$ представляет собой синусоиду с амплитудой 3 и периодом $2\pi$. Это стандартная синусоида, только с увеличенной амплитудой.

График функции будет выглядеть следующим образом:

• При $x = 0$ мы получаем $y = 3 \sin(0) = 0$.
• При $x = \frac{\pi}{2}$ мы получаем $y = 3 \sin\left(\frac{\pi}{2}\right) = 3$.
• При $x = \pi$ мы получаем $y = 3 \sin(\pi) = 0$.
• При $x = \frac{3\pi}{2}$ мы получаем $y = 3 \sin\left(\frac{3\pi}{2}\right) = -3$.
• При $x = 2\pi$ мы получаем $y = 3 \sin(2\pi) = 0$.

Функция будет колебаться между значениями $-3$ и $3$, повторяя этот цикл каждые $2\pi$.

б) $y = \frac{\cos^3 x}{2 \sin^2 x — 2} = \frac{\cos^3 x}{-2(1 — \sin^2 x)} = -\frac{\cos^3 x}{-2 \cos^2 x} = -\frac{1}{2} \cos x$

1) Преобразование выражения

Исходное выражение:

$$y = \frac{\cos^3 x}{2 \sin^2 x — 2}$$

Начнем с того, что можно вынести общий множитель из знаменателя:

$$y = \frac{\cos^3 x}{2 (\sin^2 x — 1)} = \frac{\cos^3 x}{-2 \cos^2 x}.$$

Здесь мы использовали тождество $\sin^2 x = 1 — \cos^2 x$, так что $\sin^2 x — 1 = -\cos^2 x$, и таким образом получили:

$$y = -\frac{\cos^3 x}{2 \cos^2 x}.$$

Теперь сокращаем $\cos^2 x$ в числителе и знаменателе (при условии, что $\cos x \neq 0$):

$$y = -\frac{1}{2} \cos x.$$

Это и есть окончательное преобразованное выражение.

2) Условия, при которых выражение имеет смысл

Для того, чтобы выражение было определено, знаменатель не должен быть равен нулю.

• В исходной функции мы видим, что в знаменателе содержится $\cos^2 x$, поэтому выражение имеет смысл только при $\cos x \neq 0$. Это означает, что $x \neq \pm \frac{\pi}{2} + 2\pi n$, где $n$ — целое число. Эти точки исключаются из области определения, так как в них $\cos x = 0$, и выражение становится неопределенным.

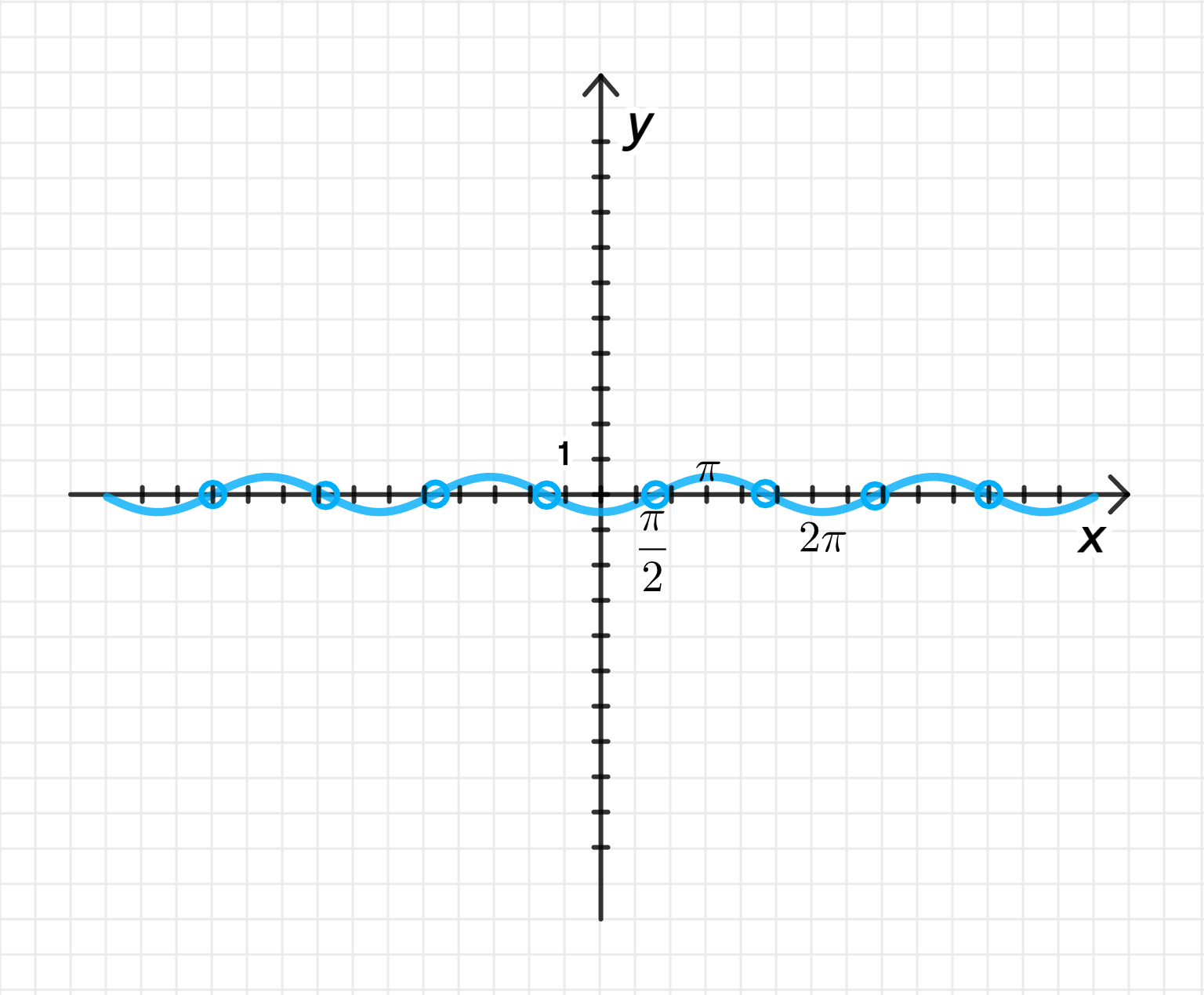
3) График функции

Функция $y = -\frac{1}{2} \cos x$ представляет собой косинусоиду с амплитудой $\frac{1}{2}$ и периодом $2\pi$. Это обычная косинусоидальная функция, но с уменьшенной амплитудой и перевернутым знаком (отрицательное значение).

• При $x = 0$ мы получаем $y = -\frac{1}{2} \cos(0) = -\frac{1}{2}$.
• При $x = \frac{\pi}{2}$ мы получаем $y = -\frac{1}{2} \cos\left(\frac{\pi}{2}\right) = 0$.
• При $x = \pi$ мы получаем $y = -\frac{1}{2} \cos(\pi) = \frac{1}{2}$.
• При $x = \frac{3\pi}{2}$ мы получаем $y = -\frac{1}{2} \cos\left(\frac{3\pi}{2}\right) = 0$.
• При $x = 2\pi$ мы получаем $y = -\frac{1}{2} \cos(2\pi) = -\frac{1}{2}$.

График функции будет колебаться между $-\frac{1}{2}$ и $\frac{1}{2}$, повторяя этот цикл каждые $2\pi$.