ГДЗ по Алгебре 10 Класс Номер 17.18 Профильный Уровень Мордкович — Подробные Ответы

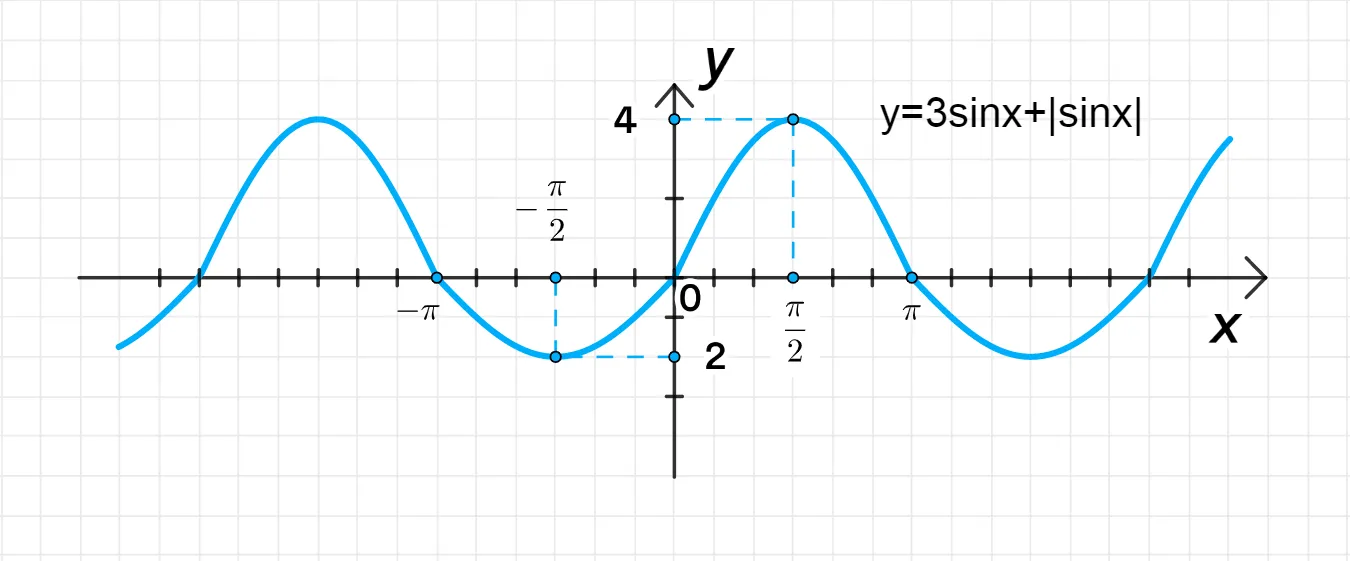
а) у = 3sinx + |sinх|;

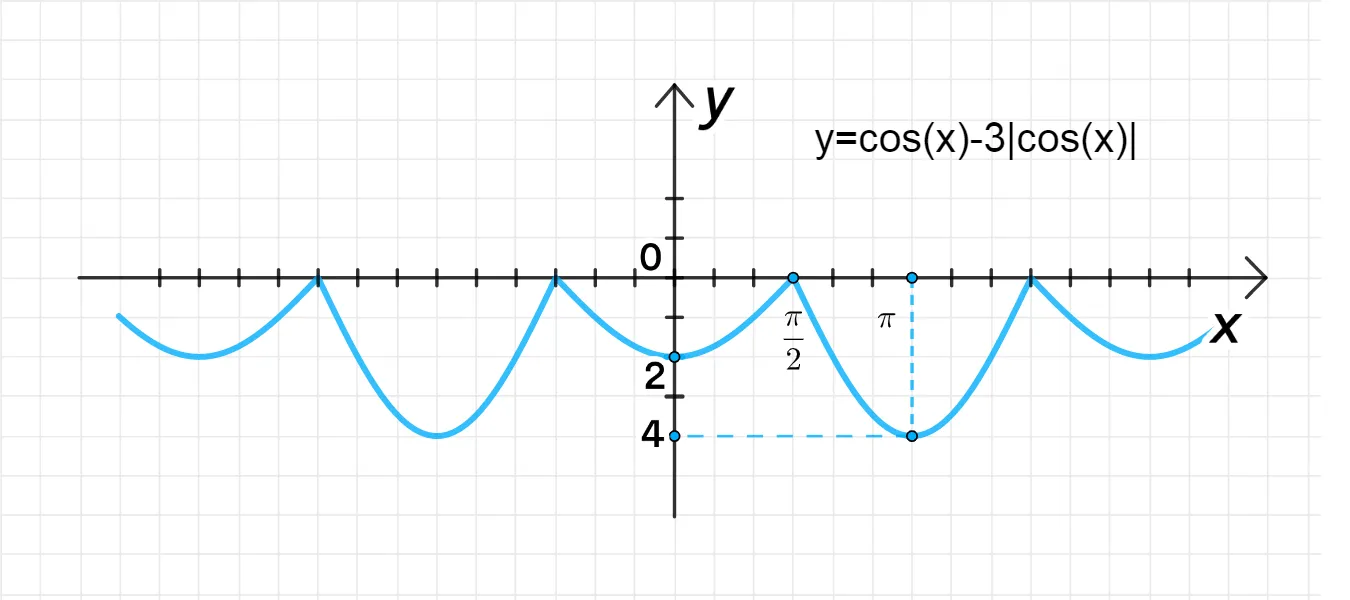
б) у = cosx — 3|cosx|.

а) $y = 3 \sin x + |\sin x|$;

Если $\sin x \geq 0$, тогда:

$$y = 3 \sin x + \sin x = 4 \sin x ;$$

Если $\sin x < 0$, тогда:

$$y = 3 \sin x — \sin x = 2 \sin x ;$$

График функции:

б) $y = \cos x — 3|\cos x|$;

Если $\cos x \geq 0$, тогда:

$$y = \cos x — 3 \cos x = -2 \cos x ;$$

Если $\cos x < 0$, тогда:

$$y = \cos x + 3 \cos x = 4 \cos x ;$$

График функции:

а) $y = 3 \sin x + |\sin x|$

1) Разбор функции

Функция включает абсолютную величину, что означает, что выражение будет зависеть от того, положительное или отрицательное значение имеет $\sin x$. Мы разобьем эту функцию на два случая:

Случай 1: $\sin x \geq 0$

Если $\sin x \geq 0$, то $|\sin x| = \sin x$. Подставляем это в выражение для $y$:

$$y = 3 \sin x + \sin x = 4 \sin x.$$

Значит, в интервале, где $\sin x \geq 0$, функция будет представлять собой обычную синусоиду с амплитудой 4.

Случай 2: $\sin x < 0$

Если $\sin x < 0$, то $|\sin x| = -\sin x$. Подставляем это в выражение для $y$:

$$y = 3 \sin x — \sin x = 2 \sin x.$$

Значит, в интервале, где $\sin x < 0$, функция будет представлять собой синусоиду с амплитудой 2.

2) График функции

График функции будет состоять из двух частей:

• В интервале, где $\sin x \geq 0$, график будет следовать за функцией $y = 4 \sin x$.
• В интервале, где $\sin x < 0$, график будет следовать за функцией $y = 2 \sin x$.

Таким образом, график функции будет иметь «перелом» на тех точках, где $\sin x = 0$ (в точках кратных $\pi$):

• При $x = 0, \pi, 2\pi, \dots$ значение функции будет $y = 0$.
• При $x = \frac{\pi}{2}, \frac{3\pi}{2}, \dots$ значения функции будут $y = 4$ или $y = -2$, в зависимости от того, где функция принимает положительные или отрицательные значения.

б) $y = \cos x — 3|\cos x|$

1) Разбор функции

Как и в предыдущем случае, функция включает абсолютную величину. Разделим её на два случая в зависимости от значения $\cos x$.

Случай 1: $\cos x \geq 0$

Если $\cos x \geq 0$, то $|\cos x| = \cos x$. Подставляем это в выражение для $y$:

$$y = \cos x — 3 \cos x = -2 \cos x.$$

Значит, в интервале, где $\cos x \geq 0$, функция будет представлять собой косинусоиду с амплитудой 2 и перевернутым знаком (умножена на -2).

Случай 2: $\cos x < 0$

Если $\cos x < 0$, то $|\cos x| = -\cos x$. Подставляем это в выражение для $y$:

$$y = \cos x + 3 \cos x = 4 \cos x.$$

Значит, в интервале, где $\cos x < 0$, функция будет представлять собой косинусоиду с амплитудой 4.

2) График функции

График функции будет выглядеть следующим образом:

• В интервале, где $\cos x \geq 0$, график будет следовать за функцией $y = -2 \cos x$.
• В интервале, где $\cos x < 0$, график будет следовать за функцией $y = 4 \cos x$.

Значения функции будут меняться в зависимости от знака $\cos x$:

• При $x = 0, 2\pi, 4\pi, \dots$ значение функции будет $y = -2$, так как $\cos x = 1$ в этих точках.
• При $x = \pi, 3\pi, 5\pi, \dots$ значение функции будет $y = 4$, так как $\cos x = -1$ в этих точках.

Таким образом, график будет колебаться между значениями $-2$ и $4$, но с перевернутым знаком в интервалах, где $\cos x \geq 0$.