ГДЗ по Алгебре 10 Класс Номер 17.19 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \frac{1}{\sin x} + \frac{1}{|\sin x|}$;

Если $\sin x > 0$, тогда:

$$y = \frac{1}{\sin x} + \frac{1}{\sin x} = 2 \cdot \frac{1}{\sin x};$$

Если $\sin x < 0$, тогда:

$$y = \frac{1}{\sin x} — \frac{1}{\sin x} = 0;$$

Выражение имеет смысл при:

$$\sin x \neq 0;$$ $$x \neq \pi n;$$

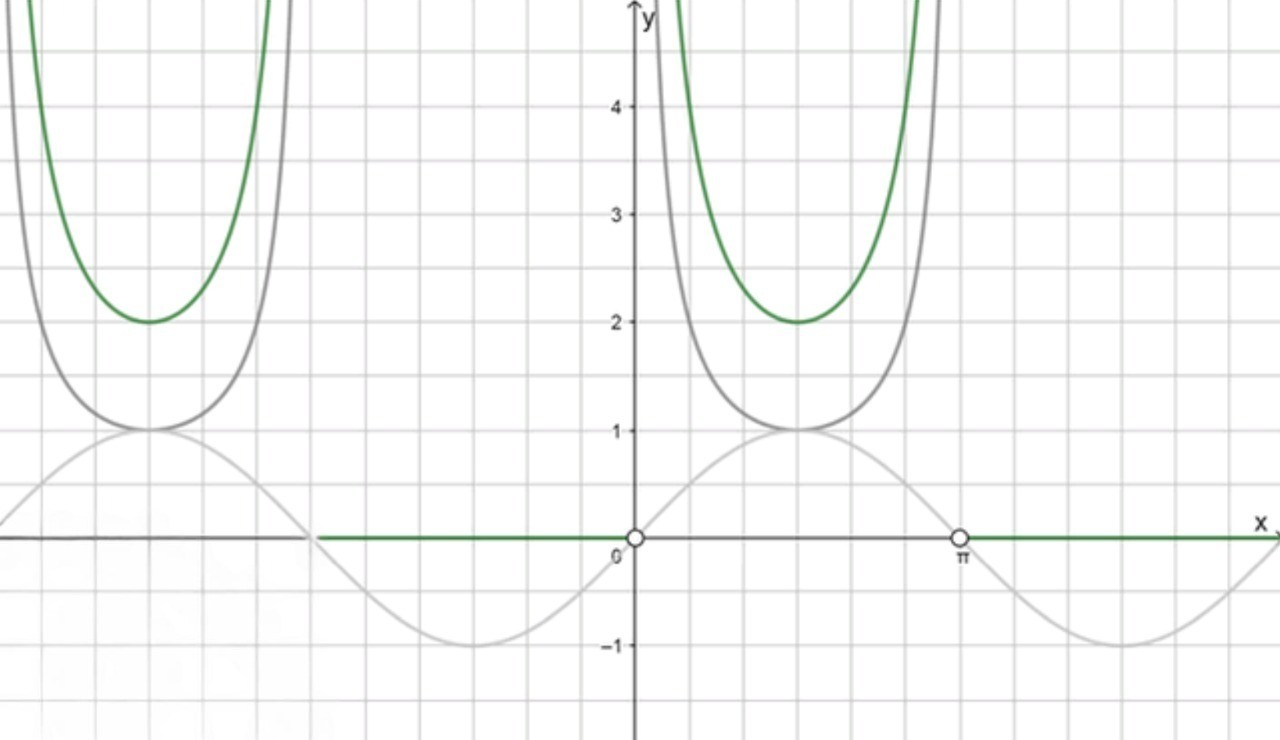
График функции:

б) $y = \frac{2}{\cos x} + \frac{1}{|\cos x|}$;

Если $\cos x > 0$, тогда:

$$y = \frac{2}{\cos x} + \frac{1}{\cos x} = 3 \cdot \frac{1}{\cos x};$$

Если $\cos x < 0$, тогда:

$$y = \frac{2}{\cos x} — \frac{1}{\cos x} = \frac{1}{\cos x};$$

Выражение имеет смысл при:

$$\cos x \neq 0;$$ $$x \neq \pm \frac{\pi}{2} + 2\pi n;$$

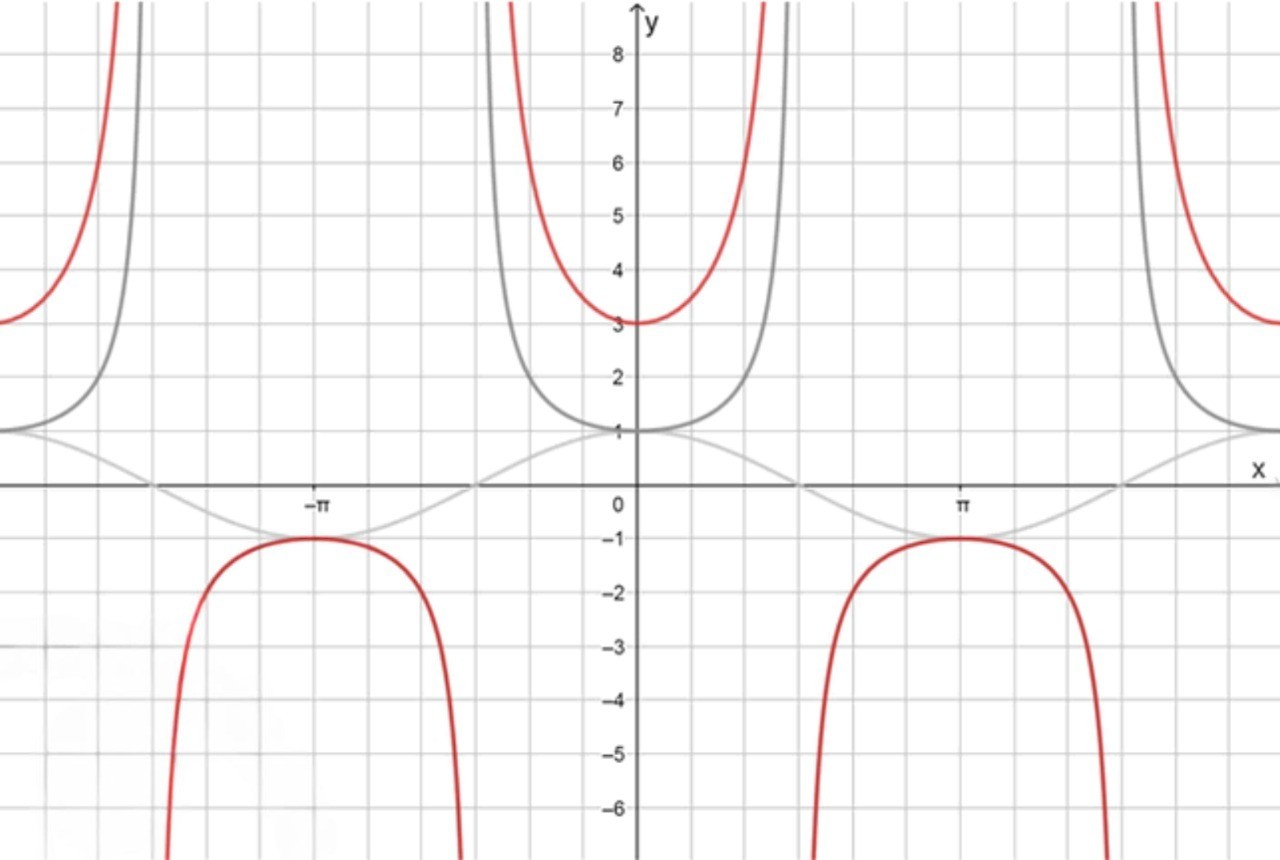
График функции:

а) $y = \frac{1}{\sin x} + \frac{1}{|\sin x|}$

1) Разбор выражения

Это выражение содержит дроби с тригонометрической функцией $\sin x$, и одна из дробей включает абсолютную величину $|\sin x|$. Чтобы точно решить выражение, необходимо рассматривать два случая, так как абсолютная величина меняет знак выражения в зависимости от значения $\sin x$.

Случай 1: $\sin x > 0$

Если $\sin x > 0$, то $|\sin x| = \sin x$, так как абсолютная величина числа всегда равна самому числу, если оно положительное. Подставляем это в выражение для $y$:

$$y = \frac{1}{\sin x} + \frac{1}{\sin x} = 2 \cdot \frac{1}{\sin x}.$$

Таким образом, если $\sin x > 0$, функция $y$ будет равна $2 \cdot \frac{1}{\sin x}$. Это выражение имеет вид гиперболы, которая стремится к бесконечности, когда $\sin x$ приближается к нулю, и уходит к нулю, когда $\sin x$ увеличивается.

Случай 2: $\sin x < 0$

Если $\sin x < 0$, то $|\sin x| = -\sin x$, так как абсолютная величина числа всегда положительная, а $\sin x$ в этом случае отрицательна. Подставляем это в выражение для $y$:

$$y = \frac{1}{\sin x} — \frac{1}{\sin x} = 0.$$

Таким образом, если $\sin x < 0$, функция $y$ будет равна 0. Это означает, что в интервалах, где $\sin x$ отрицательно, значение функции всегда будет равно нулю.

2) Условия, при которых выражение имеет смысл

Для того чтобы выражение было определено, знаменатели в обеих дробях не могут быть равны нулю. То есть, выражение будет иметь смысл, если $\sin x \neq 0$. Поскольку $\sin x = 0$ при $x = n\pi$, где $n$ — целое число, то из этого следует, что выражение имеет смысл при:

$$\sin x \neq 0;$$ $$x \neq \pi n.$$

Таким образом, $x$ не может быть кратным $\pi$, так как в этих точках $\sin x = 0$, и выражение станет неопределенным.

3) График функции

График функции будет зависеть от того, где $\sin x$ положительно или отрицательно:

• В интервале, где $\sin x > 0$ (то есть, в интервалах $(0, \pi), (2\pi, 3\pi), \dots$), график функции будет следовать за гиперболой $y = 2 \cdot \frac{1}{\sin x}$, что означает, что функция будет иметь бесконечность в точках, где $\sin x$ стремится к нулю (например, в точках $x = 0, \pi, 2\pi, \dots$).
• В интервале, где $\sin x < 0$ (то есть, в интервалах $(\pi, 2\pi), (3\pi, 4\pi), \dots$), график функции будет равен 0, то есть это будет горизонтальная линия $y = 0$.

Функция будет периодичной с периодом $2\pi$, так как $\sin x$ имеет период $2\pi$.

б) $y = \frac{2}{\cos x} + \frac{1}{|\cos x|}$

1) Разбор выражения

Аналогично первому случаю, здесь также есть дроби с тригонометрической функцией $\cos x$, и одна из дробей включает абсолютную величину $|\cos x|$. Для того чтобы разобраться, нужно рассматривать два случая в зависимости от знака $\cos x$.

Случай 1: $\cos x > 0$

Если $\cos x > 0$, то $|\cos x| = \cos x$, так как абсолютная величина положительного числа равна самому числу. Подставляем это в выражение для $y$:

$$y = \frac{2}{\cos x} + \frac{1}{\cos x} = 3 \cdot \frac{1}{\cos x}.$$

Таким образом, если $\cos x > 0$, функция $y$ будет равна $3 \cdot \frac{1}{\cos x}$. Это выражение также будет иметь гиперболическую форму, и она будет стремиться к бесконечности, когда $\cos x$ приближается к нулю.

Случай 2: $\cos x < 0$

Если $\cos x < 0$, то $|\cos x| = -\cos x$, так как абсолютная величина всегда положительная. Подставляем это в выражение для $y$:

$$y = \frac{2}{\cos x} — \frac{1}{\cos x} = \frac{1}{\cos x}.$$

Таким образом, если $\cos x < 0$, функция $y$ будет равна $\frac{1}{\cos x}$.

2) Условия, при которых выражение имеет смысл

Для того чтобы выражение было определено, знаменатели в обеих дробях не могут быть равны нулю. То есть, выражение имеет смысл, если $\cos x \neq 0$. Поскольку $\cos x = 0$ при $x = \pm \frac{\pi}{2} + 2\pi n$, где $n$ — целое число, из этого следует, что выражение имеет смысл при:

$$\cos x \neq 0;$$ $$x \neq \pm \frac{\pi}{2} + 2\pi n.$$

Таким образом, $x$ не может быть равно $\pm \frac{\pi}{2} + 2\pi n$, так как в этих точках $\cos x = 0$, и выражение станет неопределенным.

3) График функции

График функции будет зависеть от того, где $\cos x$ положительно или отрицательно:

• В интервале, где $\cos x > 0$ (то есть, в интервалах $(-\frac{\pi}{2}, \frac{\pi}{2}), (3\pi, 5\pi), \dots$), график функции будет следовать за гиперболой $y = 3 \cdot \frac{1}{\cos x}$, что означает, что функция будет иметь бесконечность в точках, где $\cos x$ стремится к нулю (например, в точках $x = \frac{\pi}{2}, \frac{3\pi}{2}, \dots$).
• В интервале, где $\cos x < 0$ (то есть, в интервалах $(\frac{\pi}{2}, \frac{3\pi}{2}), (\frac{5\pi}{2}, \frac{7\pi}{2}), \dots$), график функции будет следовать за гиперболой $y = \frac{1}{\cos x}$, и, как и в предыдущем случае, функция будет стремиться к бесконечности в точках, где $\cos x$ приближается к нулю.

Функция будет периодичной с периодом $2\pi$, так как $\cos x$ имеет период $2\pi$.