ГДЗ по Алгебре 10 Класс Номер 17.2 Профильный Уровень Мордкович — Подробные Ответы

а) $y=-2(x-1{)}^3$;

б) $y=3\mathrm{\mid }x+2\mathrm{\mid }$;

в) $y=-2\sqrt{x-3}$;

г) $y=0,5x^{-3}$

а) $y=-2(x-1{)}^3$;

Построим график функции $y=x^3$:

Переместим его на 1 единицу вправо вдоль оси абсцисс;

Отразим график относительно оси абсцисс;

Совершим растяжение графика от оси $Ox$ с коэффициентом $k=2$;

б) $y=3\mathrm{\mid }x+2\mathrm{\mid }$;

Построим график функции $y=\mathrm{\mid }x\mathrm{\mid }$:

Переместим его на 2 единицы влево вдоль оси абсцисс;

Совершим растяжение графика от оси $Ox$ с коэффициентом $k=3$;

в) $y=-2\sqrt{x-3}$;

Построим график функции $y=\sqrt{x}$:

Переместим его на 3 единицы вправо вдоль оси абсцисс;

Отразим график относительно оси абсцисс;

Совершим растяжение графика от оси $Ox$ с коэффициентом $k=2$;

г) $y=0,5x^{-3}$;

Построим график функции $y=\frac{1}{x^3}$:

Совершим сжатие графика к оси $Ox$ с коэффициентом $k=2$;

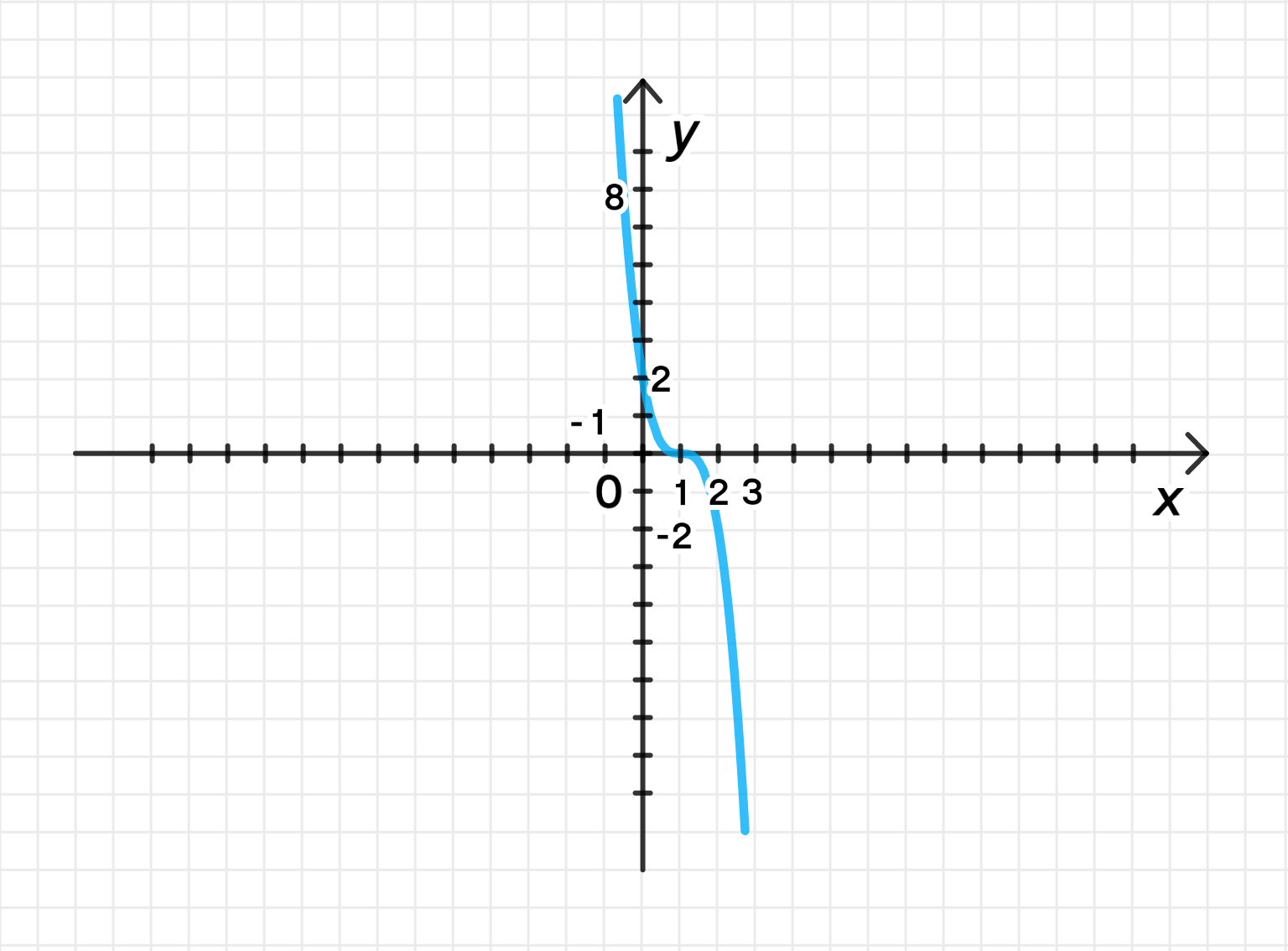
а) $y=-2(x-1{)}^3$

1) Построим график функции $y=x^3$

График функции $y=x^3$ представляет собой кубическую кривую. Рассмотрим несколько значений $x$ и соответствующие значения $y$:

• Когда $x=-2$, то $y=(-2{)}^3=-8$;
• Когда $x=-1$, то $y=(-1{)}^3=-1$;
• Когда $x=0$, то $y=0^3=0$;
• Когда $x=1$, то $y=1^3=1$;
• Когда $x=2$, то $y=2^3=8$.

График функции $y=x^3$ будет иметь точку перегиба в $(0,0)$ и будет выглядеть как гладкая кривая, направляющаяся вверх вправо и вниз влево.

2) Переместим его на 1 единицу вправо вдоль оси абсцисс

Чтобы переместить график функции $y=x^3$ на 1 единицу вправо, заменим $x$ на $(x-1)$, то есть новая функция будет $y=(x-1{)}^3$. Это означает, что каждая точка на графике функции $y=x^3$ будет сдвинута на 1 единицу вправо.

• Для $x=0$ в функции $y=x^3$ было $y=0$, а в функции $y=(x-1{)}^3$ при $x=1$ будет $y=0$.
• Для $x=1$ в функции $y=x^3$ было $y=1$, а для $x=2$ в функции $y=(x-1{)}^3$ будет $y=1$.

График будет сдвинут вправо, но по форме останется идентичным графику функции $y=x^3$.

3) Отразим график относительно оси абсцисс

Чтобы отразить график относительно оси абсцисс, нужно заменить знак у всей функции, то есть преобразуем $y=(x-1{)}^3$ в $y=-(x-1{)}^3$.

• Для $x=0$ в функции $y=-(x-1{)}^3$ значение $y=-(0-1{)}^3=-(-1{)}^3=1$.
• Для $x=1$ значение $y=-(1-1{)}^3=0$.
• Для $x=2$ значение $y=-(2-1{)}^3=-(1^3)=-1$.

Теперь весь график будет отражен относительно оси $y=0$, то есть все положительные значения $y$ станут отрицательными и наоборот.

4) Совершим растяжение графика от оси $Ox$ с коэффициентом $k=2$

Растяжение графика функции по оси $y$ с коэффициентом 2 означает, что каждый $y$ будет умножен на 2. Таким образом, функция $y=-2(x-1{)}^3$ будет иметь следующие изменения:

• Для $x=0$ значение $y=2\times 1=2$.
• Для $x=1$ значение $y=2\times 0=0$.
• Для $x=2$ значение $y=2\times (-1)=-2$.

График станет более «крутым», то есть будет растянут по оси $y$ в 2 раза, и его «амплитуда» увеличится.

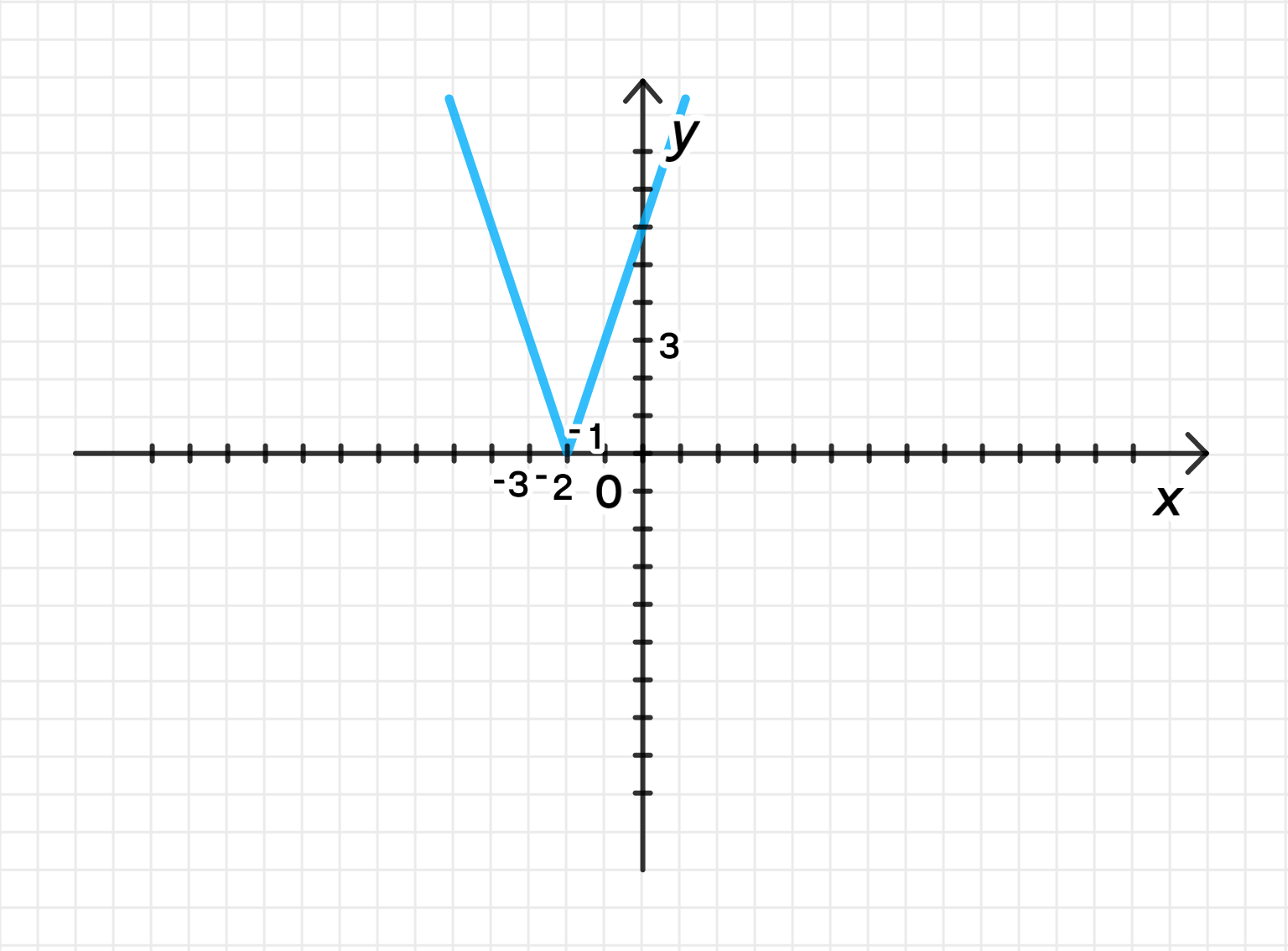
б) $y=3\mathrm{\mid }x+2\mathrm{\mid }$

1) Построим график функции $y=\mathrm{\mid }x\mathrm{\mid }$

График функции $y=\mathrm{\mid }x\mathrm{\mid }$ представляет собой «V»-образную фигуру с вершиной в точке $(0,0)$. Рассмотрим несколько значений:

График будет симметричен относительно оси $y$, и каждый $y$ для положительных $x$ будет равен $x$, а для отрицательных $x$ — равен $-x$.

2) Переместим его на 2 единицы влево вдоль оси абсцисс

Чтобы переместить график функции $y=\mathrm{\mid }x\mathrm{\mid }$ на 2 единицы влево, заменим $x$ на $(x+2)$, то есть новая функция будет $y=\mathrm{\mid }x+2\mathrm{\mid }$.

• Для $x=-2$, значение $y=0$ (вершина «V»);
• Для $x=-1$, значение $y=1$;
• Для $x=0$, значение $y=2$.

График сдвинется влево на 2 единицы.

3) Совершим растяжение графика от оси $Ox$ с коэффициентом $k=3$

Для растяжения графика по оси $y$ на коэффициент 3, нужно умножить все значения функции на 3. Это приведет к следующему:

• Для $x=-2$, значение $y=3\times 0=0$;
• Для $x=-1$, значение $y=3\times 1=3$;
• Для $x=0$, значение $y=3\times 2=6$.

График будет растянут в 3 раза по оси $y$, и его «высота» увеличится.

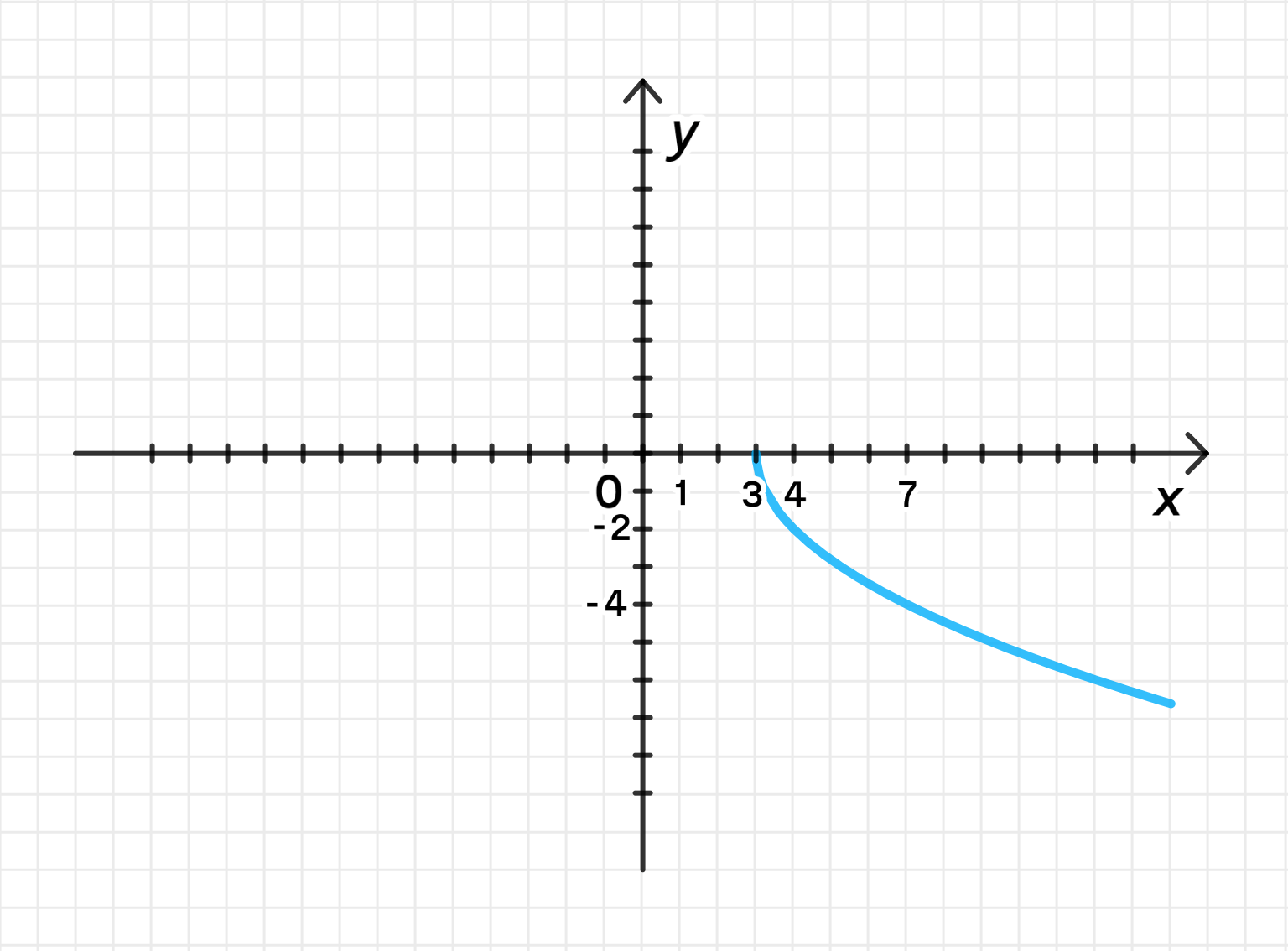
в) $y=-2\sqrt{x-3}$

1) Построим график функции $y=\sqrt{x}$

График функции $y=\sqrt{x}$ — это половина параболы, которая растет от нуля при $x=0$ и направляется вверх вправо:

График будет проходить через точки $(0,0),(1,1),(4,2)$, и далее будет продолжаться вправо.

2) Переместим его на 3 единицы вправо вдоль оси абсцисс

Чтобы переместить график функции $y=\sqrt{x}$ на 3 единицы вправо, заменим $x$ на $(x-3)$, то есть новая функция будет $y=\sqrt{x-3}$.

• Для $x=3$ в функции $y=\sqrt{x-3}$ значение $y=0$;
• Для $x=4$ значение $y=1$;
• Для $x=5$ значение $y=2$.

График сдвинется вправо на 3 единицы.

3) Отразим график относительно оси абсцисс

Отражение графика относительно оси абсцисс означает изменение знака функции на противоположный. Таким образом, функция станет $y=-\sqrt{x-3}$. Теперь график будет опускаться вниз вместо подъема.

• Для $x=3$, значение $y=0$;
• Для $x=4$, значение $y=-1$;
• Для $x=5$, значение $y=-2$.

4) Совершим растяжение графика от оси $Ox$ с коэффициентом $k=2$

Растяжение графика по оси $y$ с коэффициентом 2 означает, что каждый $y$ будет умножен на 2:

• Для $x=3$, значение $y=2\times 0=0$;
• Для $x=4$, значение $y=2\times (-1)=-2$;
• Для $x=5$, значение $y=2\times (-2)=-4$.

График станет более «крутым», и его амплитуда увеличится в 2 раза.

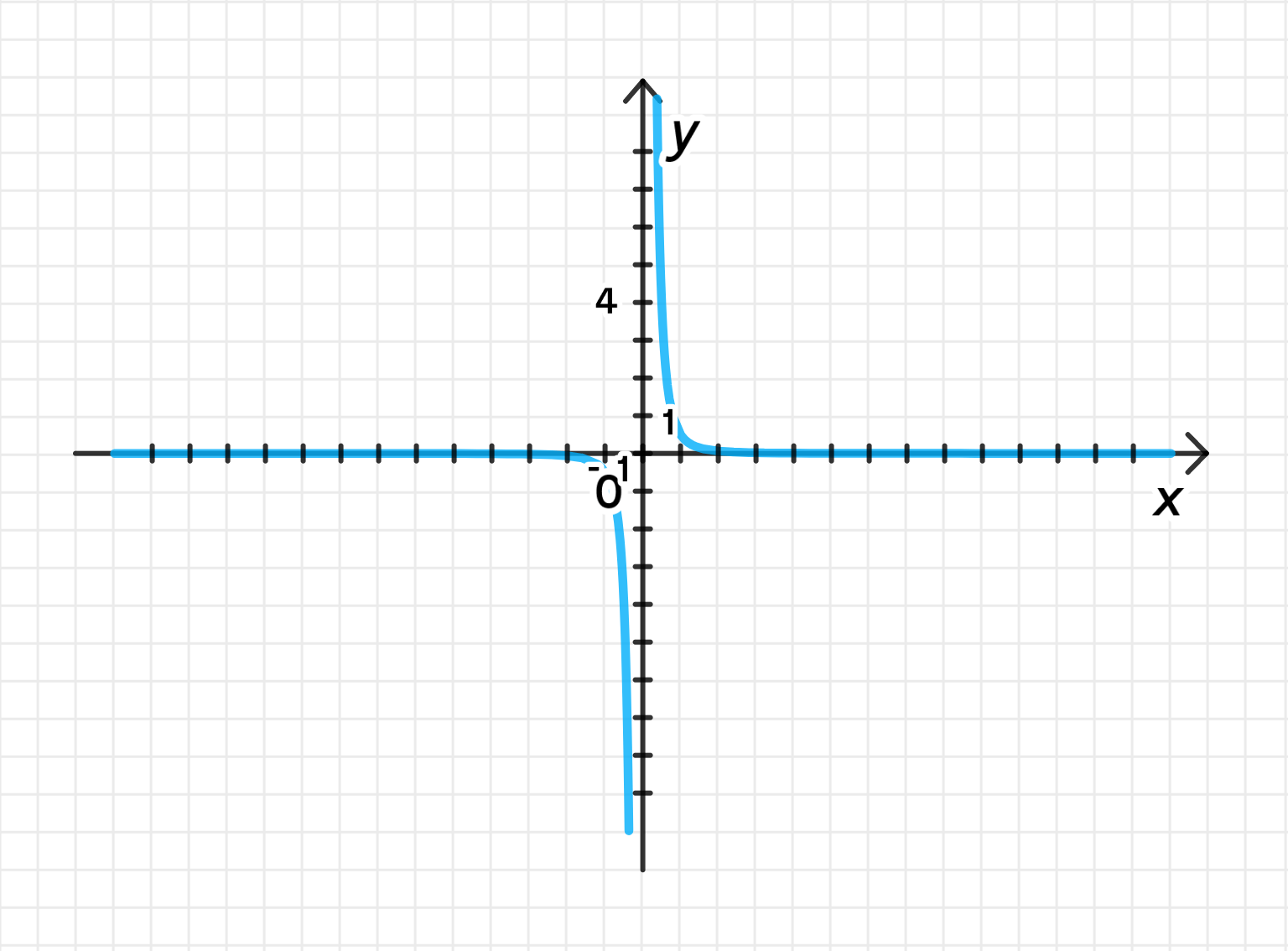
г) $y=0,5x^{-3}$

1) Построим график функции $y=\frac{1}{x^3}$

График функции $y=\frac{1}{x^3}$ представляет собой гиперболу. Рассмотрим несколько значений:

График функции имеет вертикальную асимптоту в точке $x=0$ и стремится к нулю, когда $\mathrm{\mid }x\mathrm{\mid }\to \mathrm{\infty }$.

2) Совершим сжатие графика к оси $Ox$ с коэффициентом $k=2$

Сжатие графика функции по оси $y$ с коэффициентом 2 означает, что каждое значение $y$ будет уменьшено в 2 раза. Это приведет к следующему:

• Для $x=-1$, значение $y=-1$ станет $y=-0.5$;
• Для $x=-0.5$, значение $y=-8$ станет $y=-4$;
• Для $x=0.5$, значение $y=8$ станет $y=4$;
• Для $x=1$, значение $y=1$ станет $y=0.5$.

График будет сжат в 2 раза по вертикали, и его амплитуда уменьшится.