ГДЗ по Алгебре 10 Класс Номер 17.21 Профильный Уровень Мордкович — Подробные Ответы

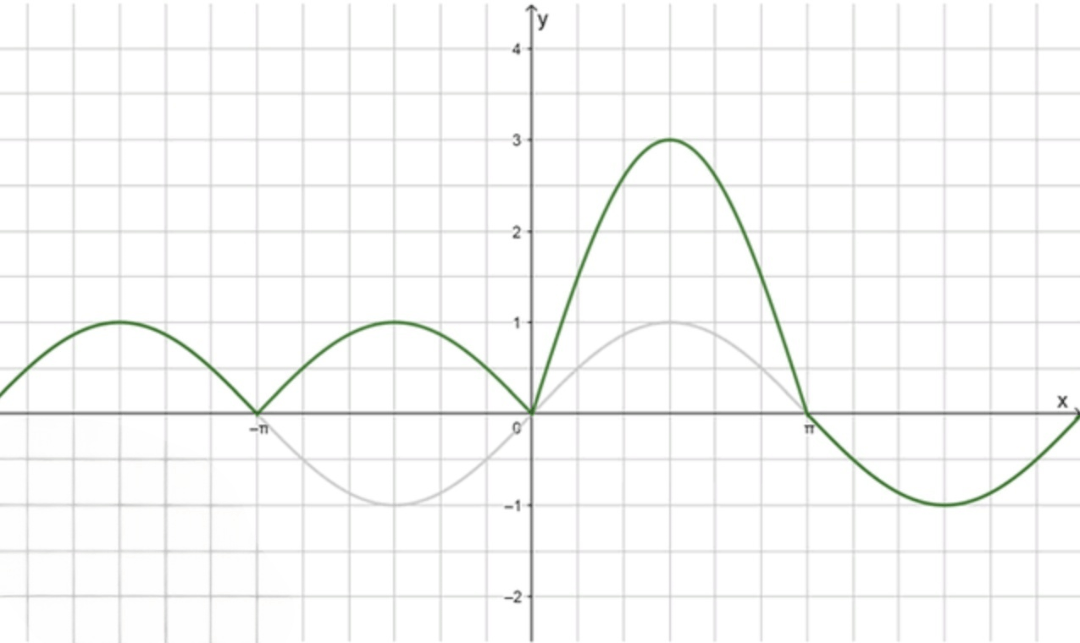
а) у = sinx + sin|x| + |sinx|;

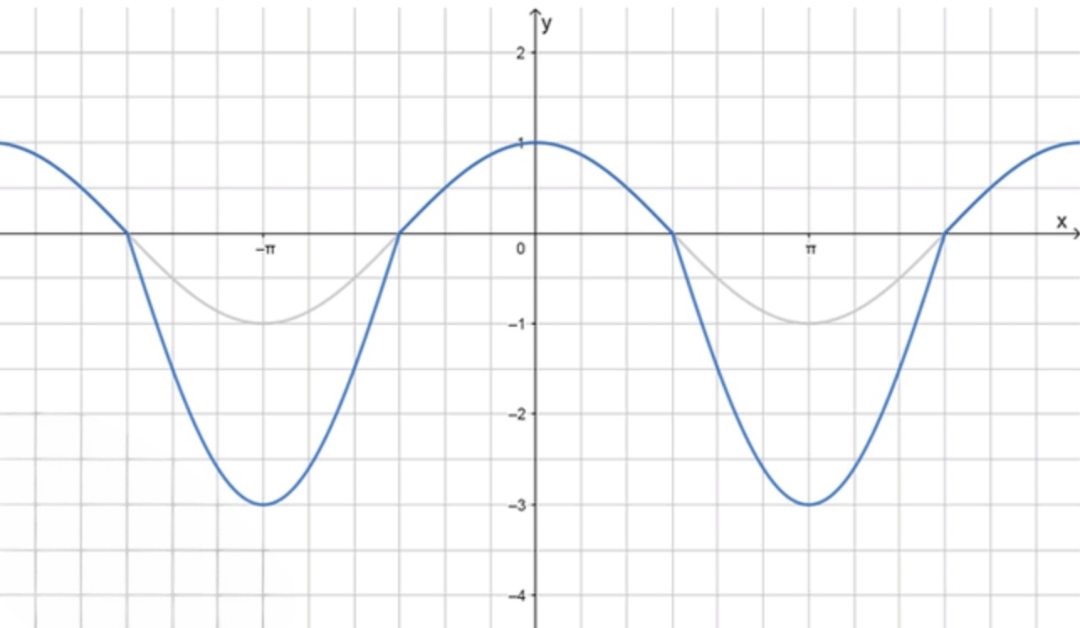
б) у = cosx + cos|x| — |cosх|.

а) $y = \sin x + \sin |x| + |\sin x|$;

Если $\begin{cases} x \geq 0 \\ \sin x \geq 0 \end{cases}$, тогда:

$$y = \sin x + \sin x + \sin x = 3 \sin x;$$

Если $\begin{cases} x \geq 0 \\ \sin x < 0 \end{cases}$, тогда:

$$y = \sin x + \sin x — \sin x = \sin x;$$

Если $\begin{cases} x < 0 \\ \sin x \geq 0 \end{cases}$, тогда:

$$y = \sin x + \sin(-x) + \sin x = \sin x;$$

Если $\begin{cases} x < 0 \\ \sin x < 0 \end{cases}$, тогда:

$$y = \sin x + \sin(-x) — \sin x = -\sin x;$$

б) $y = \cos x + \cos |x| — |\cos x|$;

Если $\begin{cases} x \geq 0 \\ \cos x \geq 0 \end{cases}$, тогда:

$$y = \cos x + \cos x — \cos x = \cos x;$$

Если $\begin{cases} x \geq 0 \\ \cos x < 0 \end{cases}$, тогда:

$$y = \cos x + \cos x + \cos x = 3 \cos x;$$

Если $\begin{cases} x < 0 \\ \cos x \geq 0 \end{cases}$, тогда:

$$y = \cos x + \cos(-x) — \cos x = \cos x;$$

Если $\begin{cases} x < 0 \\ \cos x < 0 \end{cases}$, тогда:

$$y = \cos x + \cos(-x) + \cos x = 3 \cos x;$$

а) $y = \sin x + \sin |x| + |\sin x|$

1) Разбор выражения

Это выражение включает три части: $\sin x$, $\sin |x|$ и $|\sin x|$. Чтобы корректно проанализировать поведение этой функции, необходимо учитывать два аспекта:

• $\sin |x|$ зависит от значения $x$, так как синус от абсолютного значения $|x|$ — это синус от положительного числа, независимо от того, является ли $x$ положительным или отрицательным.
• Абсолютная величина $|\sin x|$ вносит дополнительные изменения в знак функции, в зависимости от того, положительное или отрицательное значение имеет $\sin x$.

2) Разделение на случаи

Теперь давайте рассмотрим различные случаи для значений $x$, чтобы понять, как выражение будет вести себя в разных диапазонах.

Случай 1: $\begin{cases} x \geq 0 \\ \sin x \geq 0 \end{cases}$

В этом случае, $\sin x$ положительно, и абсолютная величина $|\sin x| = \sin x$, так как синус уже положителен. Поскольку $\sin |x| = \sin x$ (так как $|x| = x$ для $x \geq 0$), подставляем в выражение:

$$y = \sin x + \sin x + \sin x = 3 \sin x.$$

Таким образом, для $x \geq 0$ и $\sin x \geq 0$ функция принимает вид $y = 3 \sin x$, то есть это стандартная синусоида с амплитудой 3.

Случай 2: $\begin{cases} x \geq 0 \\ \sin x < 0 \end{cases}$

В этом случае, $\sin x$ отрицателен, и $|\sin x| = -\sin x$ (так как абсолютная величина всегда положительна). Поскольку $|x| = x$ при $x \geq 0$, то $\sin |x| = \sin x$, и получаем:

$$y = \sin x + \sin x — \sin x = \sin x.$$

Таким образом, для $x \geq 0$ и $\sin x < 0$ функция принимает вид $y = \sin x$, то есть обычная синусоида.

Случай 3: $\begin{cases} x < 0 \\ \sin x \geq 0 \end{cases}$

В этом случае, $x$ отрицательно, но $\sin x$ положительно. Поскольку $|x| = -x$ при $x < 0$, то $\sin |x| = \sin(-x) = -\sin x$, так как синус от отрицательного аргумента равен отрицательному значению синуса от положительного аргумента. Таким образом:

$$y = \sin x + \sin(-x) + \sin x = \sin x.$$

Здесь функция сводится к обычной синусоиде $y = \sin x$, так как $\sin(-x) = -\sin x$, и результат будет равен просто $\sin x$.

Случай 4: $\begin{cases} x < 0 \\ \sin x < 0 \end{cases}$

В этом случае, $x$ отрицательно, и $\sin x$ также отрицательно. Поскольку $\sin |x| = \sin(-x) = -\sin x$, то получаем:

$$y = \sin x + \sin(-x) — \sin x = -\sin x.$$

Таким образом, для $x < 0$ и $\sin x < 0$, функция примет вид $y = -\sin x$.

3) График функции

График функции будет состоять из четырех частей:

• Для $x \geq 0$ и $\sin x \geq 0$ функция будет $y = 3 \sin x$, то есть амплитуда синусоиды будет в три раза больше.
• Для $x \geq 0$ и $\sin x < 0$ функция будет $y = \sin x$, стандартная синусоида.
• Для $x < 0$ и $\sin x \geq 0$ функция будет $y = \sin x$, также стандартная синусоида.
• Для $x < 0$ и $\sin x < 0$ функция будет $y = -\sin x$, перевернутая синусоида.

Таким образом, график будет представлять собой чередующиеся синусоиды с разными амплитудами и знаками.

б) $y = \cos x + \cos |x| — |\cos x|$

1) Разбор выражения

Это выражение также включает три части: $\cos x$, $\cos |x|$ и $|\cos x|$. Так как абсолютная величина $|\cos x|$ меняет знак функции в зависимости от того, положительное или отрицательное значение имеет $\cos x$, необходимо рассматривать все возможные случаи.

2) Разделение на случаи

Случай 1: $\begin{cases} x \geq 0 \\ \cos x \geq 0 \end{cases}$

Если $\cos x \geq 0$, то $|\cos x| = \cos x$. Поскольку $\cos |x| = \cos x$, подставляем в выражение:

$$y = \cos x + \cos x — \cos x = \cos x.$$

Таким образом, когда $x \geq 0$ и $\cos x \geq 0$, функция принимает вид $y = \cos x$, то есть обычная косинусоида.

Случай 2: $\begin{cases} x \geq 0 \\ \cos x < 0 \end{cases}$

Если $\cos x < 0$, то $|\cos x| = -\cos x$. Поскольку $\cos |x| = \cos x$, подставляем в выражение:

$$y = \cos x + \cos x + \cos x = 3 \cos x.$$

Таким образом, когда $x \geq 0$ и $\cos x < 0$, функция будет $y = 3 \cos x$, то есть это косинусоида с амплитудой 3.

Случай 3: $\begin{cases} x < 0 \\ \cos x \geq 0 \end{cases}$

Если $x < 0$, но $\cos x \geq 0$, то $\cos |x| = \cos(-x) = \cos x$, так как косинус от отрицательного числа равен косинусу от положительного числа. Подставляем:

$$y = \cos x + \cos x — \cos x = \cos x.$$

Таким образом, для $x < 0$ и $\cos x \geq 0$, функция будет равна $y = \cos x$.

Случай 4: $\begin{cases} x < 0 \\ \cos x < 0 \end{cases}$

Если $x < 0$ и $\cos x < 0$, то $\cos |x| = \cos(-x) = \cos x$, так как косинус от отрицательного числа равен косинусу от положительного числа. Подставляем:

$$y = \cos x + \cos x + \cos x = 3 \cos x.$$

Таким образом, для $x < 0$ и $\cos x < 0$, функция будет $y = 3 \cos x$.

3) График функции

График функции будет:

• Для $x \geq 0$ и $\cos x \geq 0$ функция будет $y = \cos x$, стандартная косинусоида.
• Для $x \geq 0$ и $\cos x < 0$ функция будет $y = 3 \cos x$, амплитуда будет в три раза больше.
• Для $x < 0$ и $\cos x \geq 0$ функция будет $y = \cos x$.
• Для $x < 0$ и $\cos x < 0$ функция будет $y = 3 \cos x$.

График будет представлять собой чередующиеся косинусоиды с разными амплитудами и знаками.