ГДЗ по Алгебре 10 Класс Номер 17.22 Профильный Уровень Мордкович — Подробные Ответы

а) $y=\cos x+\cos \frac{x-\mathrm{\mid }x\mathrm{\mid }}{2}+\mathrm{\mid }\cos x\mathrm{\mid }$;

Если $\{\begin{array}{l}x\ge 0\\ \cos x\ge 0\end{array}$, тогда:

$$y=\cos x+\cos \frac{x-x}{2}+\cos x=2\cos x+\cos 0=2\cos x+1;$$

Если $\{\begin{array}{l}x\ge 0\\ \cos x<0\end{array}$, тогда:

$$y=\cos x+\cos \frac{x-x}{2}-\cos x=\cos 0=1;$$

Если $\{\begin{array}{l}x<0\\ \cos x\ge 0\end{array}$, тогда:

$$y=\cos x+\cos \frac{x+x}{2}+\cos x=2\cos x+\cos x=3\cos x;$$

Если $\{\begin{array}{l}x<0\\ \cos x<0\end{array}$, тогда:

$$y=\cos x+\cos \frac{x+x}{2}-\cos x=\cos x;$$

б) $y=\sin x-\sin \frac{x+\mathrm{\mid }x\mathrm{\mid }}{2}+\mathrm{\mid }\sin x\mathrm{\mid }$;

Если $\{\begin{array}{l}x\ge 0\\ \sin x\ge 0\end{array}$, тогда:

$$y=\sin x-\sin \frac{x+x}{2}+\sin x=2\sin x-\sin x=\sin x;$$

Если $\{\begin{array}{l}x\ge 0\\ \sin x<0\end{array}$, тогда:

$$y=\sin x-\sin \frac{x+x}{2}-\sin x=-\sin x;$$

Если $\{\begin{array}{l}x<0\\ \sin x\ge 0\end{array}$, тогда:

$$y=\sin x-\sin \frac{x-x}{2}+\sin x=2\sin x-\sin 0=2\sin x;$$

Если $\{\begin{array}{l}x<0\\ \sin x<0\end{array}$, тогда:

$$y=\sin x-\sin \frac{x-x}{2}-\sin x=0-\sin 0=0;$$

а) $y = \cos x + \cos \frac{x — |x|}{2} + |\cos x|$

1) Разбор выражения

Это выражение состоит из трех частей:

1. $\cos x$ — стандартная косинусоидальная функция.
2. $\cos \frac{x — |x|}{2}$ — функция, содержащая абсолютную величину, которая будет изменять аргумент косинуса в зависимости от того, является ли $x$ положительным или отрицательным.
3. $|\cos x|$ — абсолютная величина косинуса, которая всегда положительна и будет менять знак в зависимости от того, положительный или отрицательный $\cos x$.

Чтобы понять, как будет себя вести функция, разберем ее для разных случаев.

2) Разделение на случаи

Случай 1: $\begin{cases} x \geq 0 \\ \cos x \geq 0 \end{cases}$

Когда $x \geq 0$, $|x| = x$, и это означает, что $\frac{x — |x|}{2} = \frac{x — x}{2} = 0$. Таким образом:

$$\cos \frac{x — |x|}{2} = \cos 0 = 1.$$

Теперь, учитывая, что $\cos x \geq 0$, подставляем в исходное выражение:

$$y = \cos x + 1 + \cos x = 2 \cos x + 1.$$

Таким образом, при $x \geq 0$ и $\cos x \geq 0$ функция будет $y = 2 \cos x + 1$, то есть линейная модификация стандартной косинусоиды с амплитудой, умноженной на 2, и с добавлением 1 по оси $y$.

Случай 2: $\begin{cases} x \geq 0 \\ \cos x < 0 \end{cases}$

Когда $\cos x < 0$, то $|\cos x| = -\cos x$, и мы получаем следующее:

$$y = \cos x + \cos 0 — \cos x = \cos 0 = 1.$$

Таким образом, при $x \geq 0$ и $\cos x < 0$, функция будет равна $y = 1$, то есть постоянная величина.

Случай 3: $\begin{cases} x < 0 \\ \cos x \geq 0 \end{cases}$

Когда $x < 0$, $|x| = -x$, и следовательно:

$$\frac{x — |x|}{2} = \frac{x + x}{2} = x.$$

Таким образом:

$$\cos \frac{x — |x|}{2} = \cos x.$$

Подставляем в исходное выражение:

$$y = \cos x + \cos x + \cos x = 3 \cos x.$$

Таким образом, при $x < 0$ и $\cos x \geq 0$, функция будет $y = 3 \cos x$, что является модификацией стандартной косинусоиды с амплитудой, увеличенной в 3 раза.

Случай 4: $\begin{cases} x < 0 \\ \cos x < 0 \end{cases}$

Если $\cos x < 0$, то:

$$y = \cos x + \cos x — \cos x = \cos x.$$

Таким образом, при $x < 0$ и $\cos x < 0$, функция будет равна $y = \cos x$, то есть стандартная косинусоида.

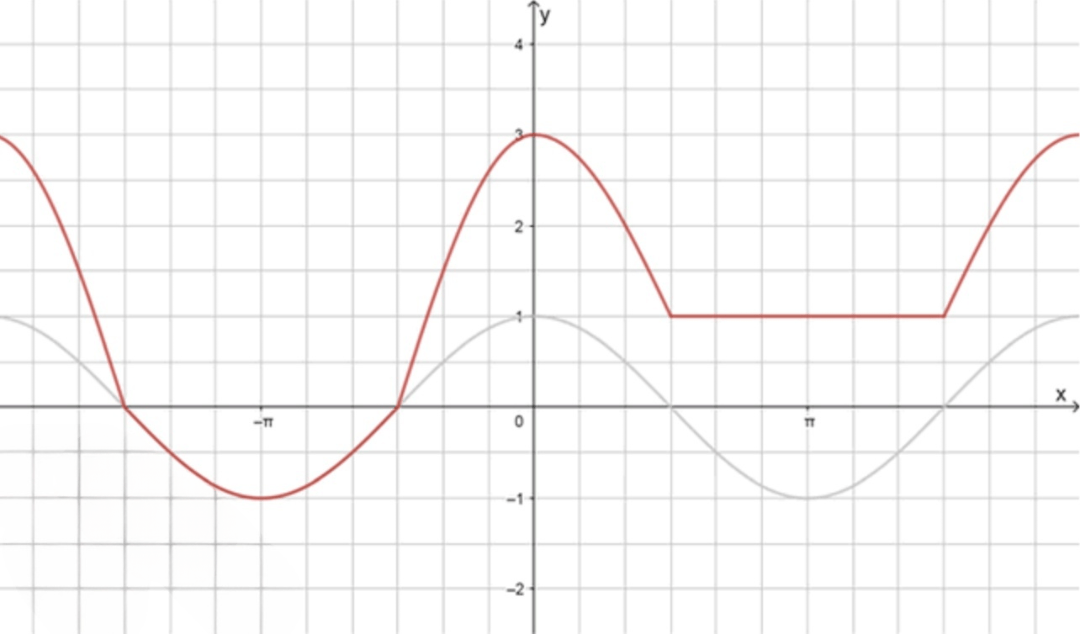
3) График функции

• Для $x \geq 0$ и $\cos x \geq 0$, график будет $y = 2 \cos x + 1$.
• Для $x \geq 0$ и $\cos x < 0$, график будет $y = 1$.
• Для $x < 0$ и $\cos x \geq 0$, график будет $y = 3 \cos x$.
• Для $x < 0$ и $\cos x < 0$, график будет $y = \cos x$.

Таким образом, график будет чередоваться между линейными преобразованиями косинусоид и постоянными значениями в зависимости от знака $\cos x$ и положения $x$.

б) $y = \sin x — \sin \frac{x + |x|}{2} + |\sin x|$

1) Разбор выражения

Это выражение также состоит из трех частей: $\sin x$, $\sin \frac{x + |x|}{2}$ и $|\sin x|$. Абсолютная величина будет менять знак, в зависимости от того, положительное или отрицательное значение имеет $\sin x$, а также будет влиять на функцию $\sin \frac{x + |x|}{2}$, так как $|x|$ изменяет аргумент функции.

2) Разделение на случаи

Случай 1: $\begin{cases} x \geq 0 \\ \sin x \geq 0 \end{cases}$

Когда $x \geq 0$ и $\sin x \geq 0$, то $|x| = x$, и:

$$\sin \frac{x + |x|}{2} = \sin \frac{x + x}{2} = \sin x.$$

Теперь, учитывая, что $|\sin x| = \sin x$, подставляем в выражение:

$$y = \sin x — \sin x + \sin x = \sin x.$$

Таким образом, при $x \geq 0$ и $\sin x \geq 0$, функция будет равна $y = \sin x$, то есть стандартная синусоида.

Случай 2: $\begin{cases} x \geq 0 \\ \sin x < 0 \end{cases}$

Когда $\sin x < 0$, то $|\sin x| = -\sin x$, и $\sin \frac{x + |x|}{2} = \sin x$, подставляем:

$$y = \sin x — \sin x — \sin x = -\sin x.$$

Таким образом, при $x \geq 0$ и $\sin x < 0$, функция будет $y = -\sin x$.

Случай 3: $\begin{cases} x < 0 \\ \sin x \geq 0 \end{cases}$

Когда $x < 0$, $|x| = -x$, и:

$$\sin \frac{x + |x|}{2} = \sin \frac{x — x}{2} = \sin 0 = 0.$$

Подставляем в исходное выражение:

$$y = \sin x — 0 + \sin x = 2 \sin x.$$

Таким образом, при $x < 0$ и $\sin x \geq 0$, функция будет $y = 2 \sin x$.

Случай 4: $\begin{cases} x < 0 \\ \sin x < 0 \end{cases}$

Если $\sin x < 0$, то $|\sin x| = -\sin x$, и $\sin \frac{x + |x|}{2} = \sin 0 = 0$, подставляем:

$$y = \sin x — 0 — \sin x = 0.$$

Таким образом, при $x < 0$ и $\sin x < 0$, функция будет равна $y = 0$.

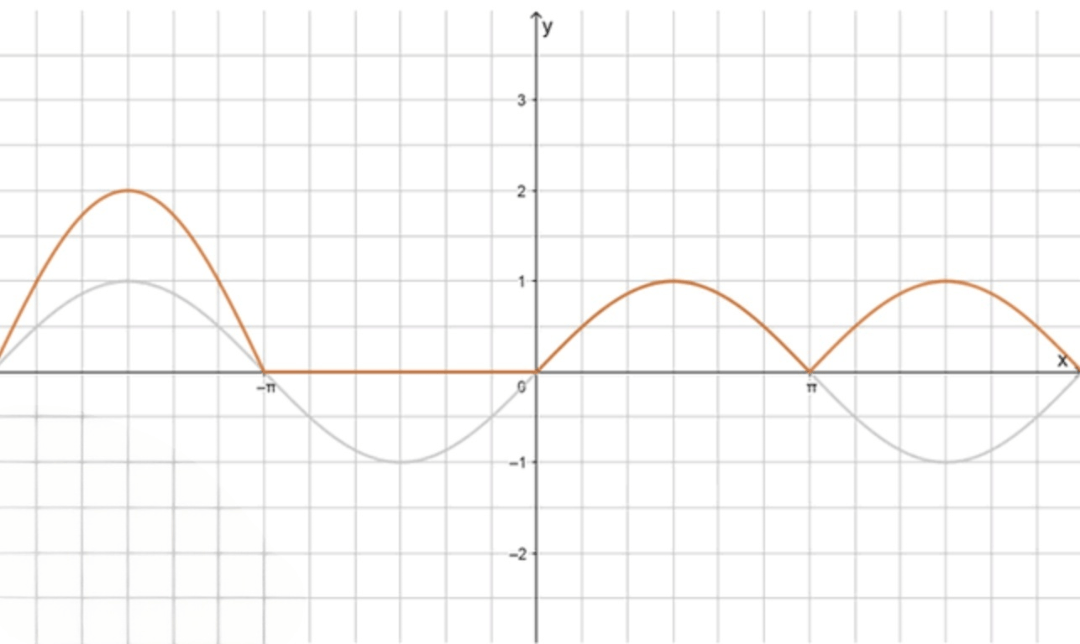
3) График функции

• Для $x \geq 0$ и $\sin x \geq 0$, график будет $y = \sin x$.
• Для $x \geq 0$ и $\sin x < 0$, график будет $y = -\sin x$.
• Для $x < 0$ и $\sin x \geq 0$, график будет $y = 2 \sin x$.
• Для $x < 0$ и $\sin x < 0$, график будет $y = 0$.

График будет представлять собой чередующиеся синусоиды с разными амплитудами и знаками в зависимости от того, является ли $\sin x$ положительным или отрицательным и от того, является ли $x$ положительным или отрицательным.