ГДЗ по Алгебре 10 Класс Номер 17.3 Профильный Уровень Мордкович — Подробные Ответы

а) $y = 2 \sin x$;

б) $y = 3 \cos x$;

в) $y = -\sin x$;

г) $y = -\cos x$

а) $y = 2 \sin x$;

Построим график функции $y = \sin x$;

Совершим растяжение графика от оси $Ox$ с коэффициентом $k = 2$:

б) $y = 3 \cos x$;

Построим график функции $y = \cos x$;

Совершим растяжение графика от оси $Ox$ с коэффициентом $k = 3$:

в) $y = -\sin x$;

Построим график функции $y = \sin x$;

Отразим график относительно оси абсцисс:

г) $y = -\cos x$;

Построим график функции $y = \cos x$;

Отразим график относительно оси абсцисс:

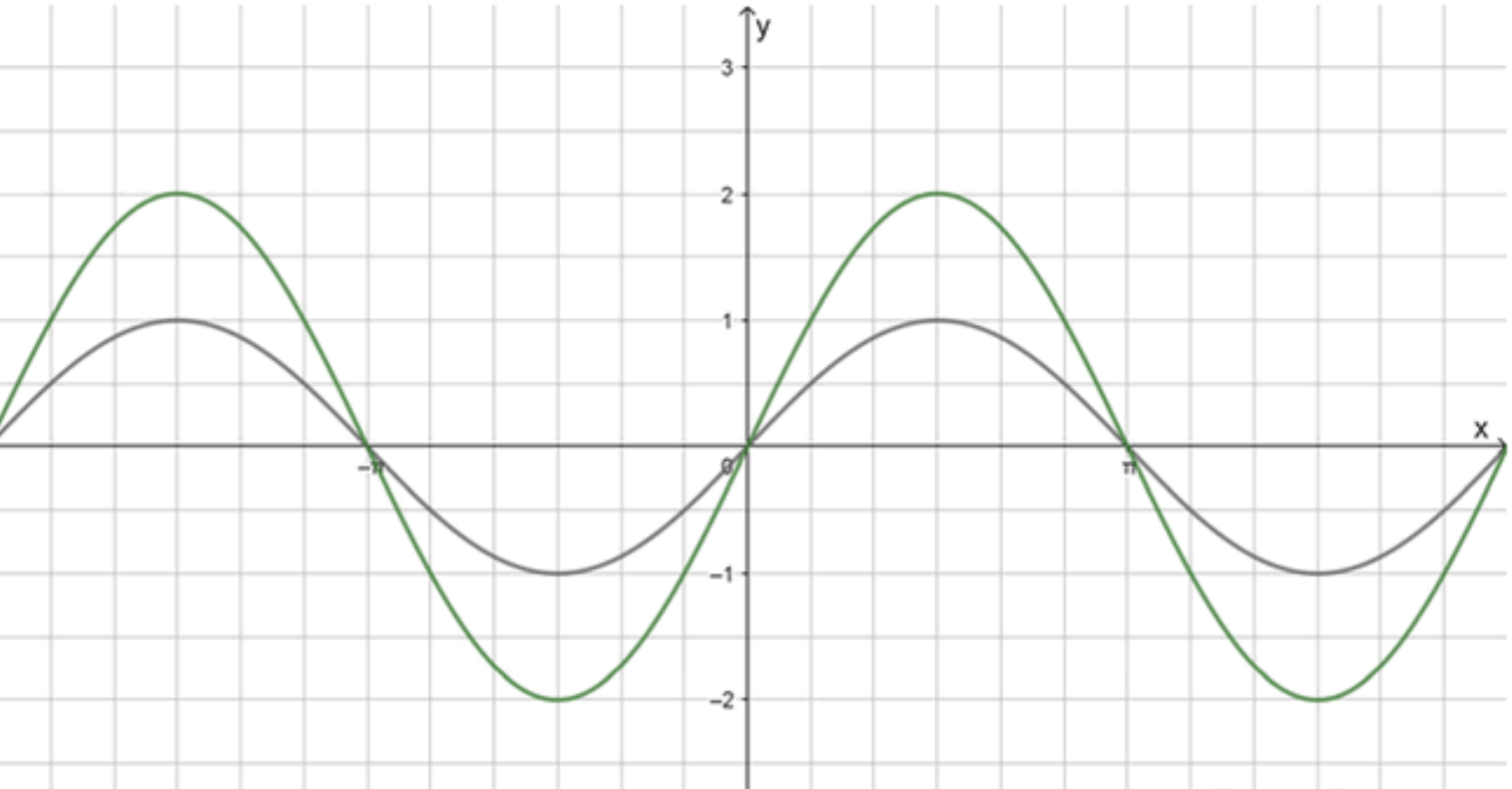
а) $y = 2 \sin x$

1) Построим график функции $y = \sin x$

Функция $y = \sin x$ является стандартной синусоидой. График этой функции представляет собой волну, которая колеблется между значениями $-1$ и $1$, с периодом $2\pi$ и амплитудой 1. Рассмотрим несколько значений функции для разных значений $x$:

Таким образом, график функции $y = \sin x$ будет выглядеть как синусоида, колеблющаяся между -1 и 1 с периодом $2\pi$, проходящая через точки $(0, 0)$, $\left( \frac{\pi}{2}, 1 \right)$, $(\pi, 0)$, $\left( \frac{3\pi}{2}, -1 \right)$, $(2\pi, 0)$.

2) Совершим растяжение графика от оси $Ox$ с коэффициентом $k = 2$

Чтобы растянуть график функции по оси $y$ с коэффициентом 2, нужно умножить все значения функции на 2. То есть, новая функция будет $y = 2 \sin x$, и для каждого значения $y$ на графике $y = \sin x$ значение будет увеличено в 2 раза.

Рассмотрим это на примере:

• Для $x = 0$, $y = 2 \times 0 = 0$.
• Для $x = \frac{\pi}{2}$, $y = 2 \times 1 = 2$.
• Для $x = \pi$, $y = 2 \times 0 = 0$.
• Для $x = \frac{3\pi}{2}$, $y = 2 \times (-1) = -2$.
• Для $x = 2\pi$, $y = 2 \times 0 = 0$.

График функции $y = 2 \sin x$ будет колебаться между значениями $-2$ и $2$, и амплитуда синусоиды увеличится в 2 раза по сравнению с графиком $y = \sin x$.

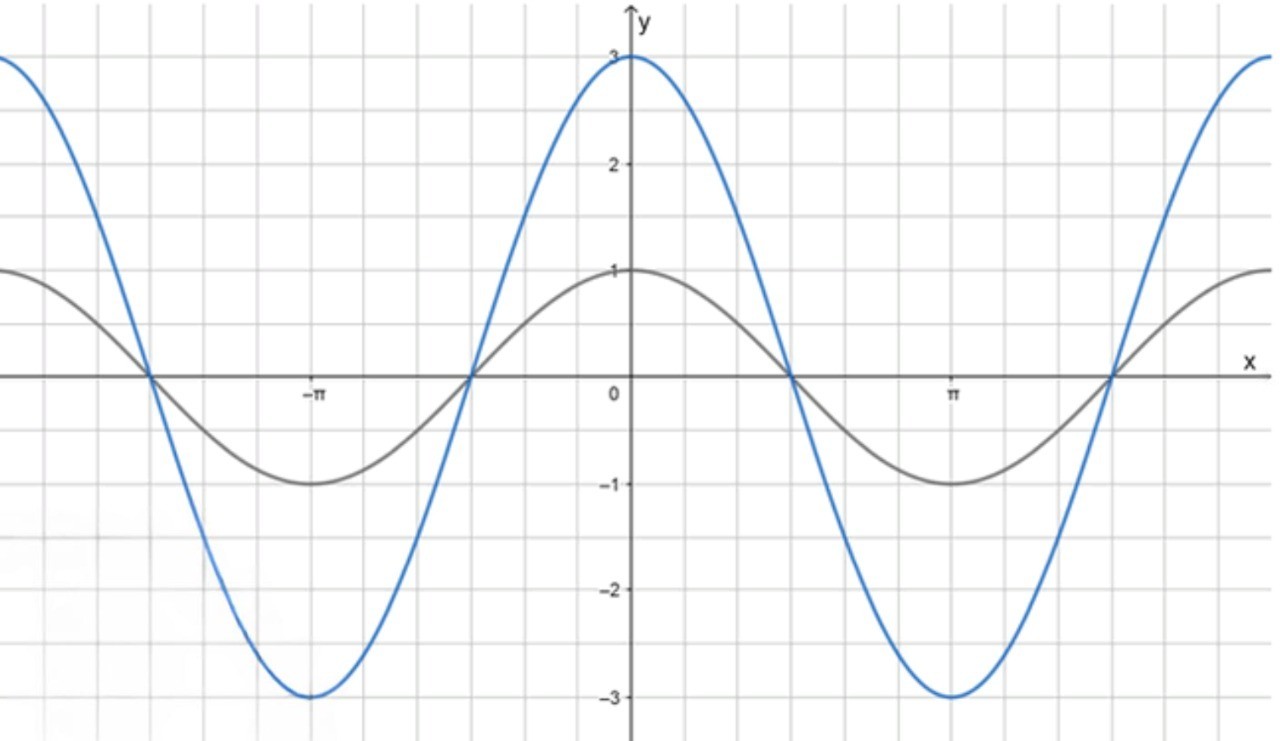
б) $y = 3 \cos x$

1) Построим график функции $y = \cos x$

График функции $y = \cos x$ также представляет собой волну (косинусоиду), но с фазовым сдвигом по сравнению с синусоидой. График функции $y = \cos x$ будет колебаться между значениями $-1$ и $1$ с периодом $2\pi$ и амплитудой 1. Рассмотрим несколько значений функции для разных значений $x$:

График функции $y = \cos x$ будет выглядеть как косинусоида, колеблющаяся между значениями -1 и 1, с периодом $2\pi$, проходящая через точки $(0, 1)$, $\left( \frac{\pi}{2}, 0 \right)$, $(\pi, -1)$, $\left( \frac{3\pi}{2}, 0 \right)$, $(2\pi, 1)$.

2) Совершим растяжение графика от оси $Ox$ с коэффициентом $k = 3$

Для растяжения графика функции по оси $y$ с коэффициентом 3, нужно умножить все значения $y$ на 3. То есть новая функция будет $y = 3 \cos x$, и для каждого значения $y$ на графике $y = \cos x$ значение будет увеличено в 3 раза.

Рассмотрим это на примере:

• Для $x = 0$, $y = 3 \times 1 = 3$.
• Для $x = \frac{\pi}{2}$, $y = 3 \times 0 = 0$.
• Для $x = \pi$, $y = 3 \times (-1) = -3$.
• Для $x = \frac{3\pi}{2}$, $y = 3 \times 0 = 0$.
• Для $x = 2\pi$, $y = 3 \times 1 = 3$.

График функции $y = 3 \cos x$ будет колебаться между значениями $-3$ и $3$, и амплитуда косинусоиды увеличится в 3 раза по сравнению с графиком $y = \cos x$.

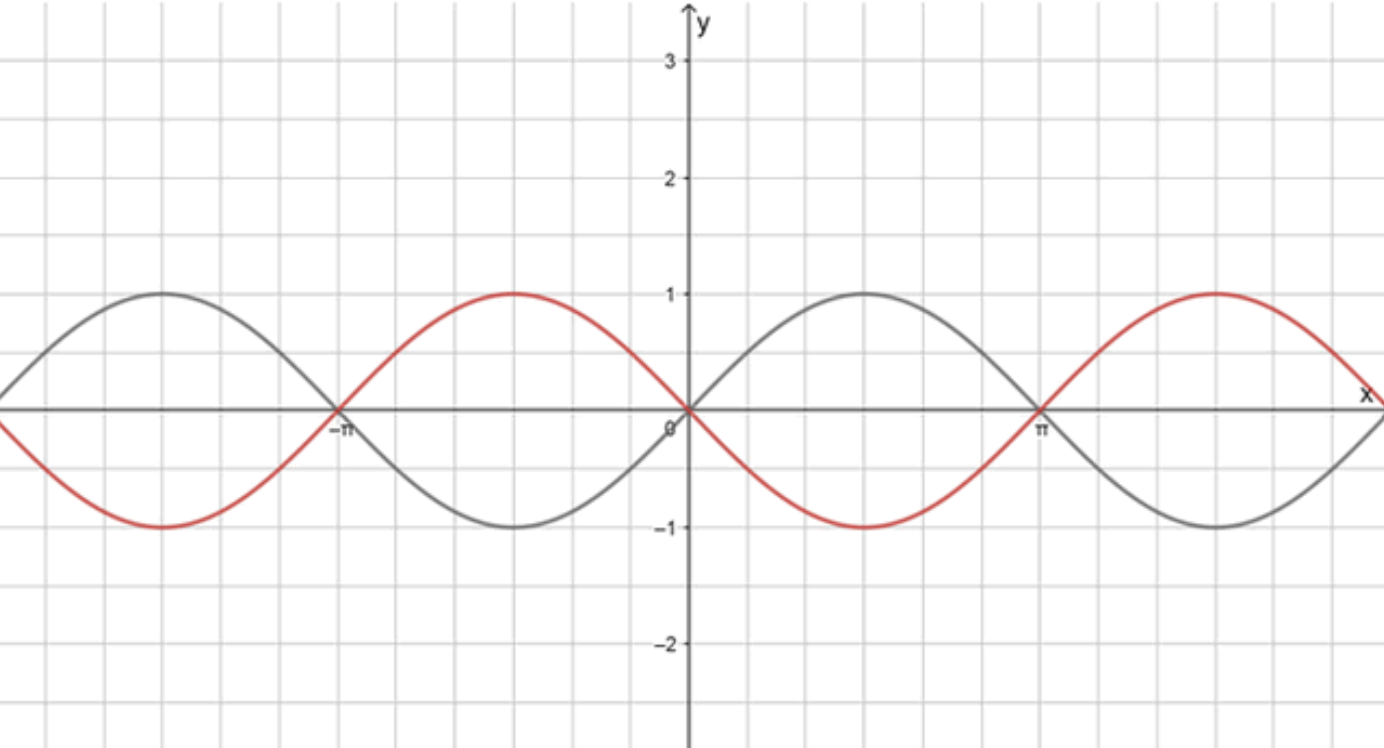
в) $y = -\sin x$

1) Построим график функции $y = \sin x$

График функции $y = \sin x$ был рассмотрен в пункте 1 для функции $y = 2 \sin x$, и он представляет собой стандартную синусоиду, колеблющуюся между $-1$ и $1$.

2) Отразим график относительно оси абсцисс

Отражение графика функции относительно оси абсцисс означает замену всех значений $y$ на противоположные. Таким образом, если для функции $y = \sin x$ значение в точке $x = 0$ равно $0$, то для функции $y = -\sin x$ это значение также будет равно $0$, но все остальные значения $y$ изменятся на противоположные.

• Для $x = 0$, $y = 0$.
• Для $x = \frac{\pi}{2}$, $y = -1$.
• Для $x = \pi$, $y = 0$.
• Для $x = \frac{3\pi}{2}$, $y = 1$.
• Для $x = 2\pi$, $y = 0$.

Теперь график будет опущен вниз, и все положительные значения функции $y = \sin x$ станут отрицательными, а все отрицательные значения — положительными.

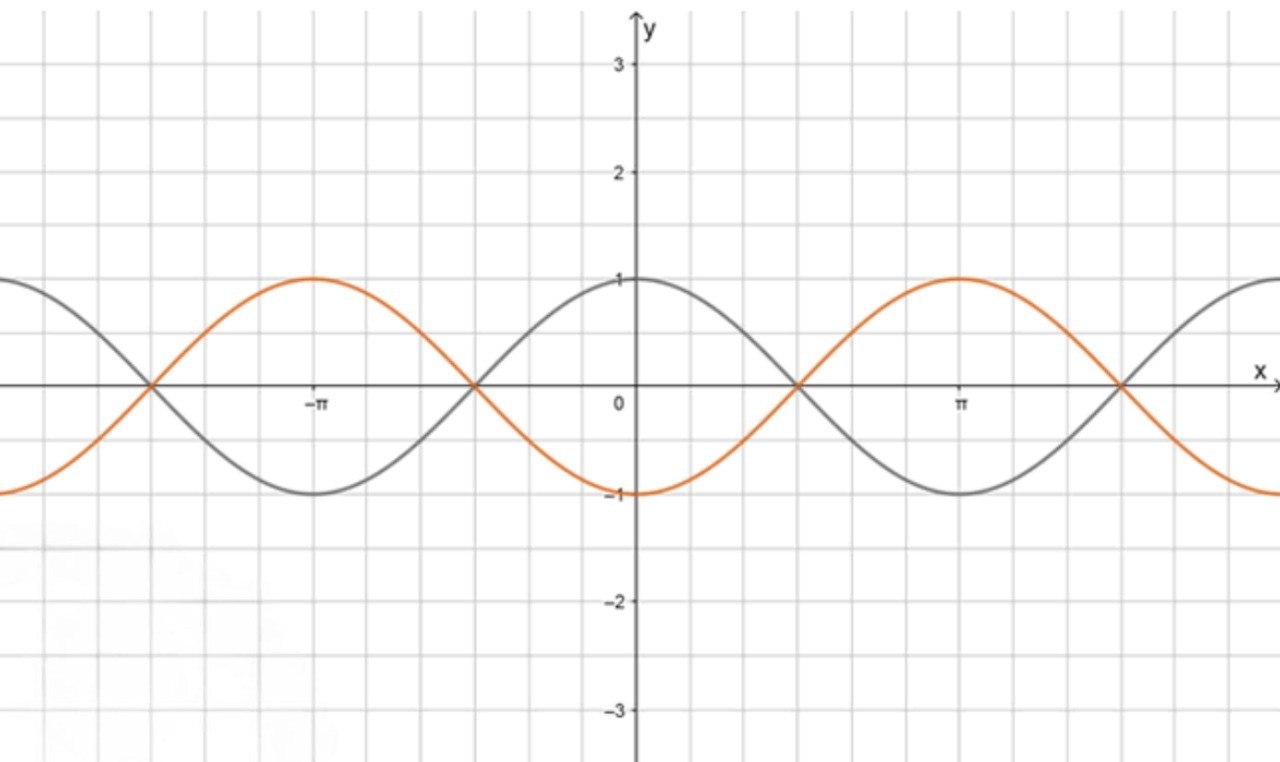
г) $y = -\cos x$

1) Построим график функции $y = \cos x$

График функции $y = \cos x$ был рассмотрен в пункте 1 для функции $y = 3 \cos x$, и он представляет собой стандартную косинусоиду, колеблющуюся между $-1$ и $1$.

2) Отразим график относительно оси абсцисс

Отражение графика функции относительно оси абсцисс также будет заключаться в замене знака у всех значений $y$. То есть для функции $y = \cos x$ заменим все значения на противоположные, получив $y = -\cos x$.

• Для $x = 0$, $y = -1$.
• Для $x = \frac{\pi}{2}$, $y = 0$.
• Для $x = \pi$, $y = 1$.
• Для $x = \frac{3\pi}{2}$, $y = 0$.
• Для $x = 2\pi$, $y = -1$.

График функции $y = -\cos x$ будет симметричен графику функции $y = \cos x$, но расположен ниже оси $x$. Все значения, которые были положительными на графике $y = \cos x$, теперь будут отрицательными.