Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 17.4 Профильный Уровень Мордкович — Подробные Ответы
а) ;
б) ;
в) ;
г)
а) ;
Построим график функции ;
Отразим график относительно оси абсцисс;
Совершим растяжение графика от оси с коэффициентом .
б) ;
Построим график функции ;
Отразим график относительно оси абсцисс;
Совершим растяжение графика от оси с коэффициентом .
в) ;
Построим график функции ;
Совершим растяжение графика от оси с коэффициентом .
г) ;
Построим график функции ;
Отразим график относительно оси абсцисс;
Совершим растяжение графика от оси с коэффициентом .
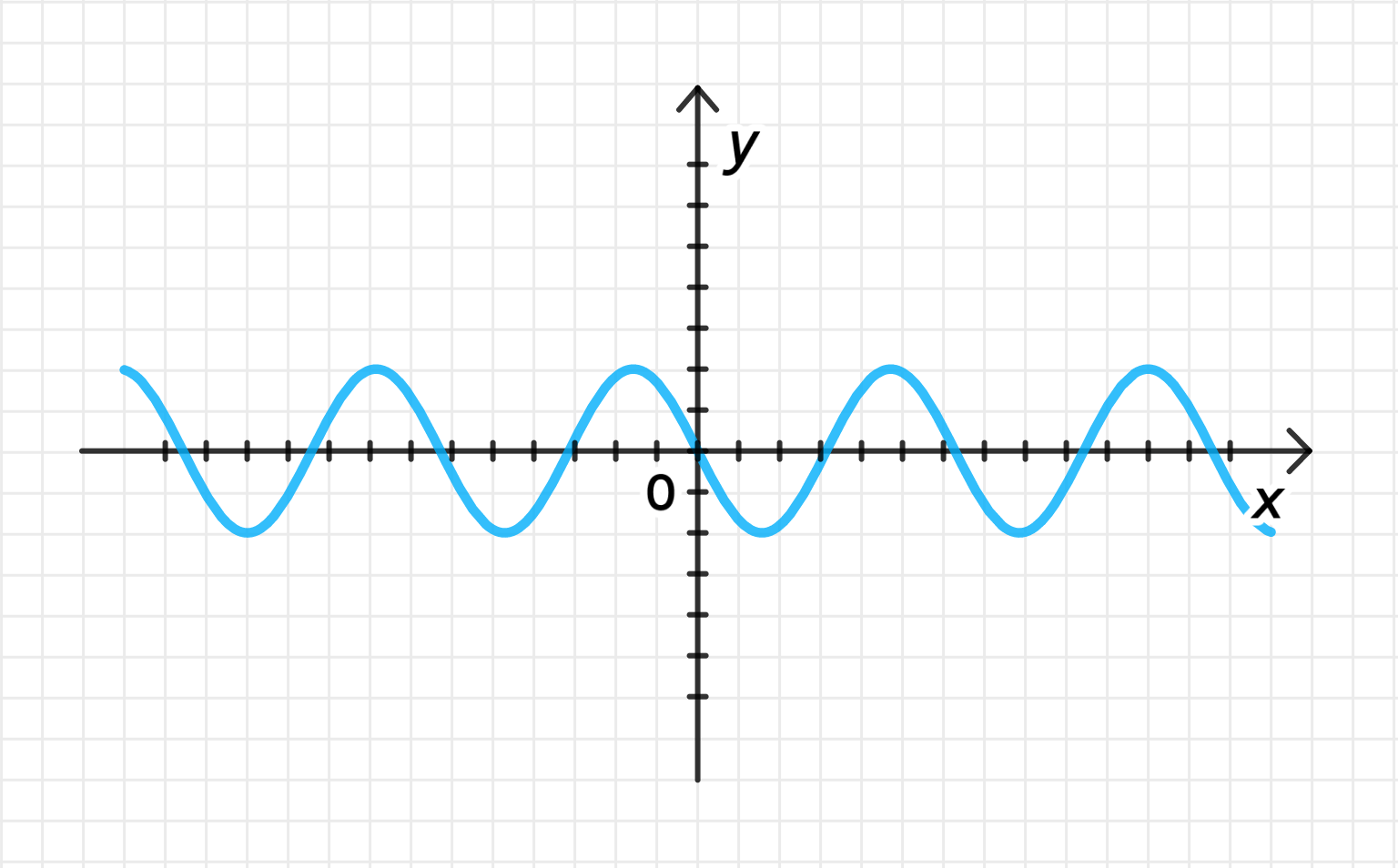
а)
1) Построим график функции
Функция — это стандартная синусоида. Рассмотрим несколько значений и соответствующие значения :
График функции представляет собой волну, которая:
- В точке принимает значение ,
- В точке принимает значение ,
- В точке принимает значение ,
- В точке принимает значение ,
- В точке снова принимает значение .
График синусоиды будет колебаться между значениями и , с периодом .
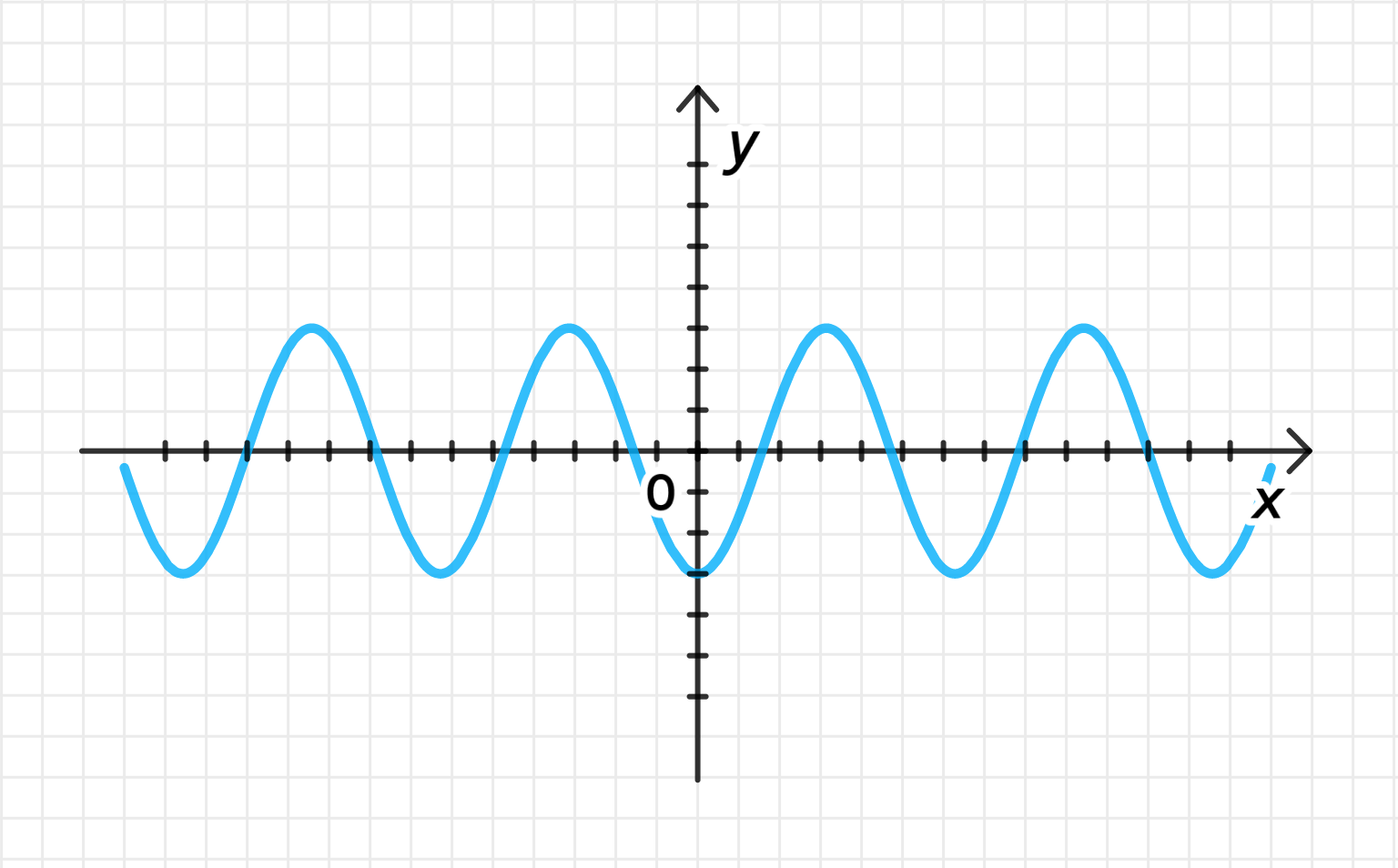
2) Отразим график относительно оси абсцисс
Отражение графика относительно оси абсцисс означает замену знака функции. Если для функции при было значение , то для отраженной функции это значение будет . Таким образом, график будет «повернут» вниз.
После отражения:
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
График функции будет точно таким же по форме, как график , но расположен ниже оси .
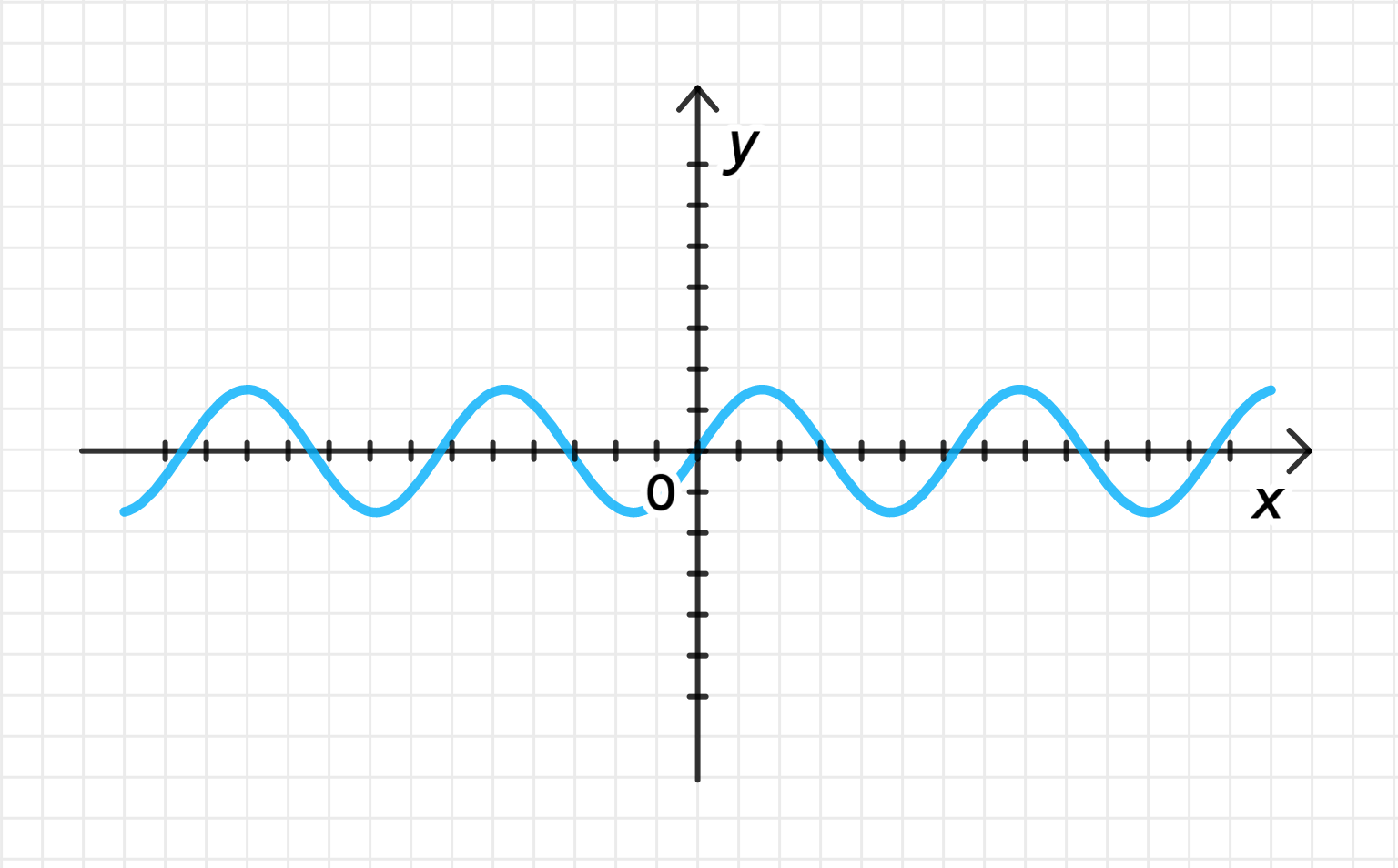
3) Совершим растяжение графика от оси с коэффициентом
Растяжение графика функции по оси с коэффициентом 2 означает, что каждый -координат будет умножен на 2. Таким образом, новая функция будет . Пример для нескольких значений :
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
График функции будет иметь амплитуду 2, то есть он будет растянут по вертикали в 2 раза.
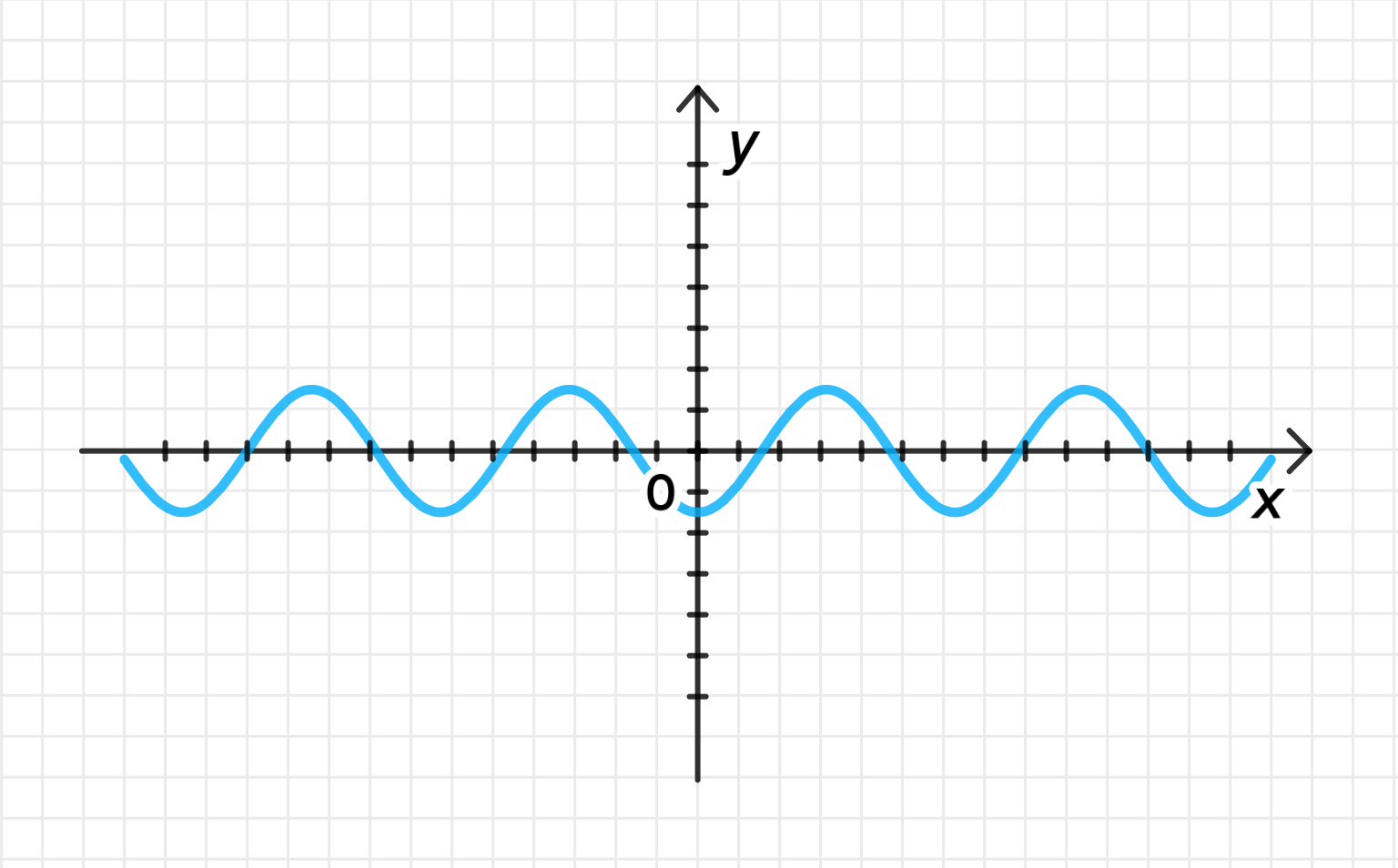
б)
1) Построим график функции
График функции является стандартной косинусоидой. Рассмотрим несколько значений и соответствующие значения :
График функции будет выглядеть как волна, колеблющаяся между значениями и с периодом . Он будет проходить через точки , , , , .
2) Отразим график относительно оси абсцисс
Отражение графика относительно оси абсцисс также будет означать изменение знака функции. Функция станет . График будет зеркально отражен вниз.
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
Теперь весь график будет располагаться ниже оси .
3) Совершим растяжение графика от оси с коэффициентом
Растяжение графика функции по оси с коэффициентом 3 означает, что все значения будут умножены на 3. Таким образом, новая функция будет . Пример для нескольких значений:
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
График функции будет иметь амплитуду 3, то есть его «высота» увеличится в 3 раза по сравнению с графиком .
в)
1) Построим график функции
График функции был рассмотрен в пункте 1 для функции , и он представляет собой стандартную синусоиду, колеблющуюся между и .
2) Совершим растяжение графика от оси с коэффициентом
Растяжение графика функции по оси с коэффициентом 1,5 означает, что каждый -координат будет умножен на 1,5. Таким образом, новая функция будет . Пример для нескольких значений:
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
График функции будет колебаться между и , и амплитуда синусоиды увеличится в 1,5 раза по сравнению с графиком .
г)
1) Построим график функции
График функции был рассмотрен в пункте 1 для функции , и он представляет собой стандартную косинусоиду, колеблющуюся между и .
2) Отразим график относительно оси абсцисс
Отражение графика относительно оси абсцисс также будет заключаться в изменении знака функции. Таким образом, функция станет . График будет отражен вниз.
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
3) Совершим растяжение графика от оси с коэффициентом
Для растяжения графика функции по оси с коэффициентом 1,5, все значения будут умножены на 1,5. Таким образом, новая функция будет . Пример для нескольких значений:
- Для , ,
- Для , ,
- Для , ,
- Для , ,
- Для , .
График функции будет иметь амплитуду 1,5, то есть его «высота» увеличится в 1,5 раза по сравнению с графиком .