ГДЗ по Алгебре 10 Класс Номер 17.9 Профильный Уровень Мордкович — Подробные Ответы

а) $y = 2 \sin \left( x + \frac{\pi}{3} \right) + 1$;

б) $y = -3 \cos \left( x — \frac{5\pi}{6} \right) — 2$;

в) $y = -1,5 \sin \left( x — \frac{2\pi}{3} \right) + 2$;

г) $y=2,5\cos (x+\frac{2\pi }{3})-1,5$

а) $y = 2 \sin \left( x + \frac{\pi}{3} \right) + 1$;

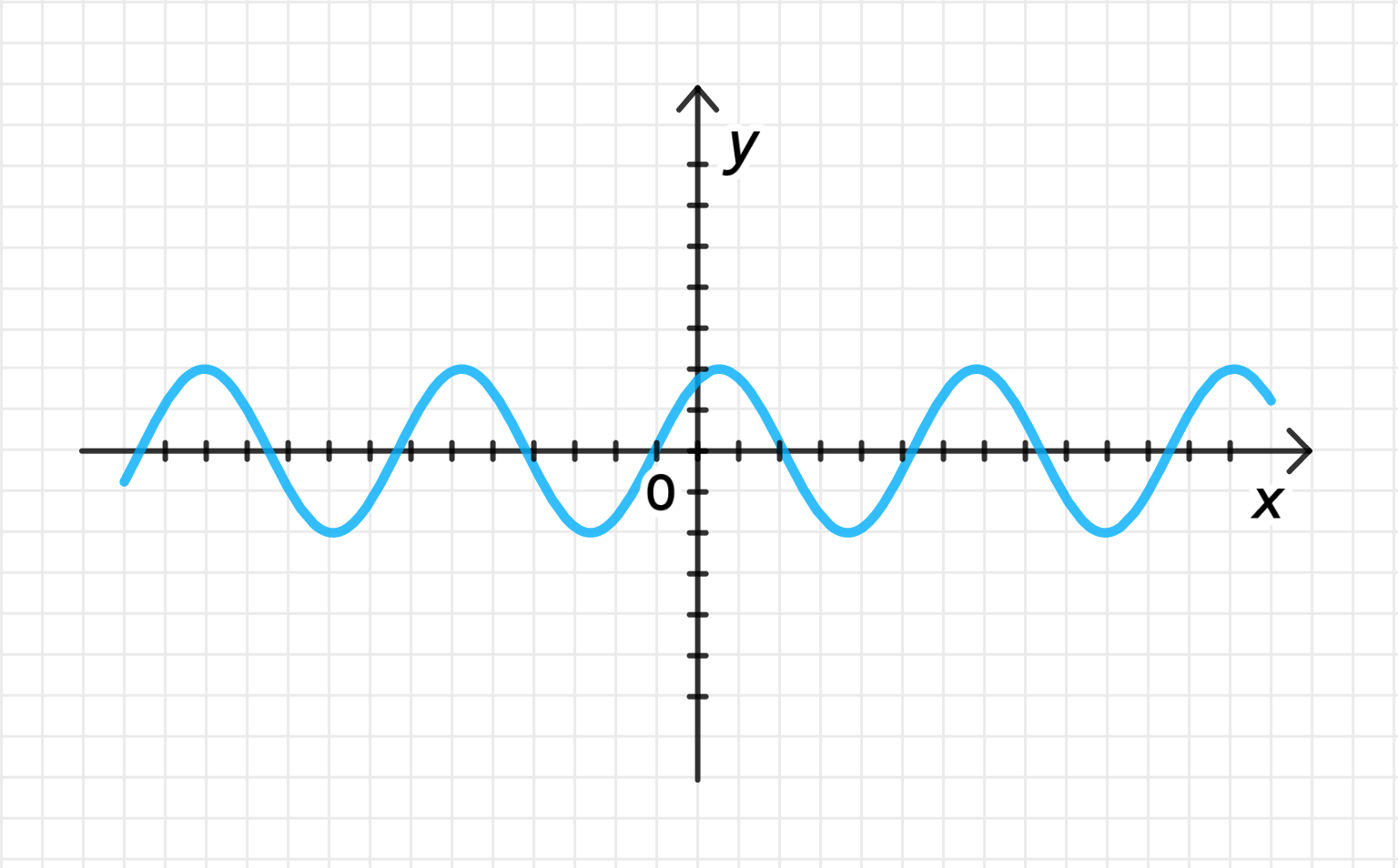
Построим дугу графика $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{3}$ единиц влево вдоль оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;
• Переместим ее на 1 единицу вверх вдоль оси ординат;

Достроим график функции:

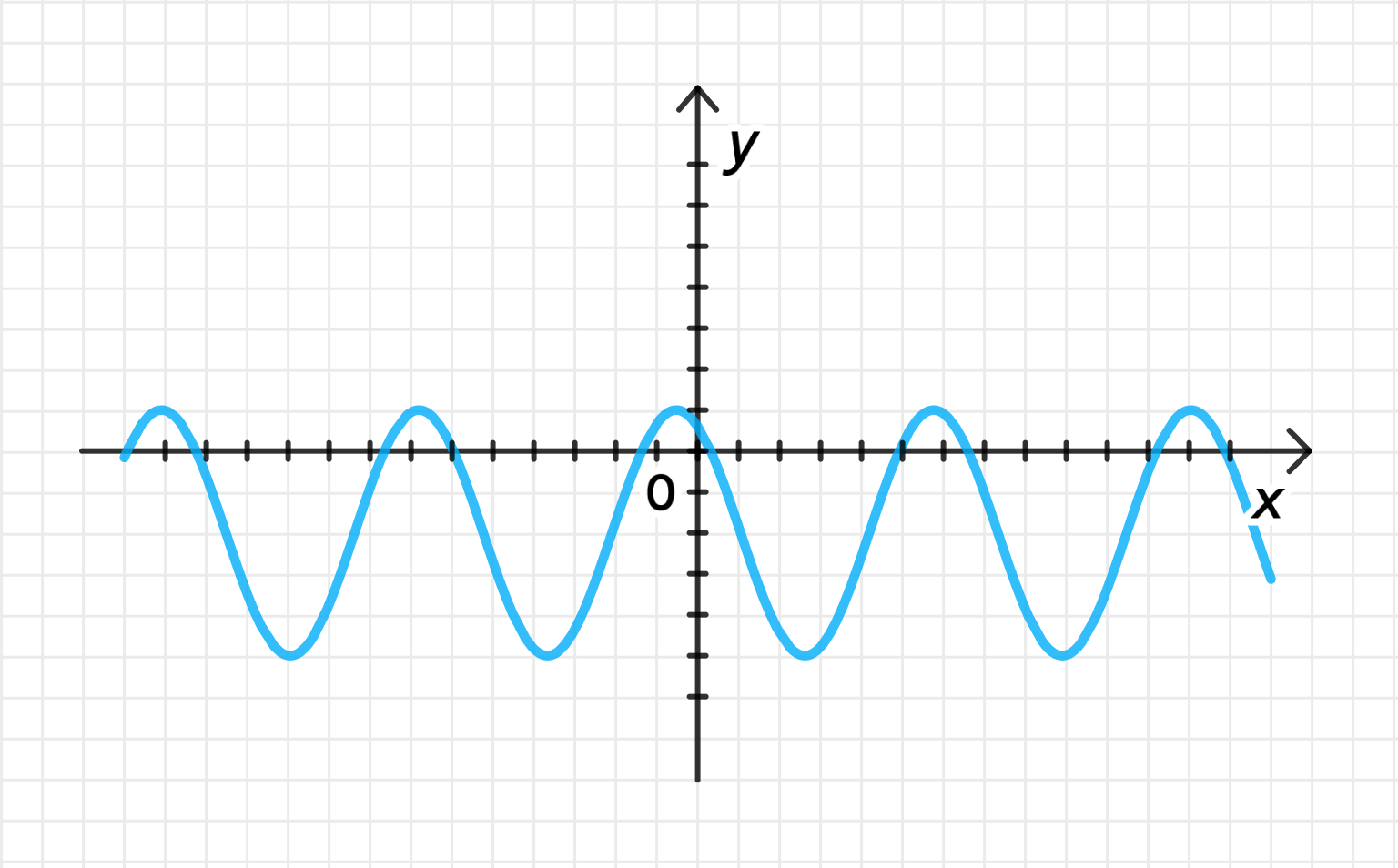
б) $y = -3 \cos \left( x — \frac{5\pi}{6} \right) — 2$;

Построим дугу графика $y = \cos x$, а затем:

• Переместим ее на $\frac{5\pi}{6}$ единиц вправо вдоль оси абсцисс;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 3$;
• Переместим ее на 2 единицы вниз вдоль оси ординат;

Достроим график функции:

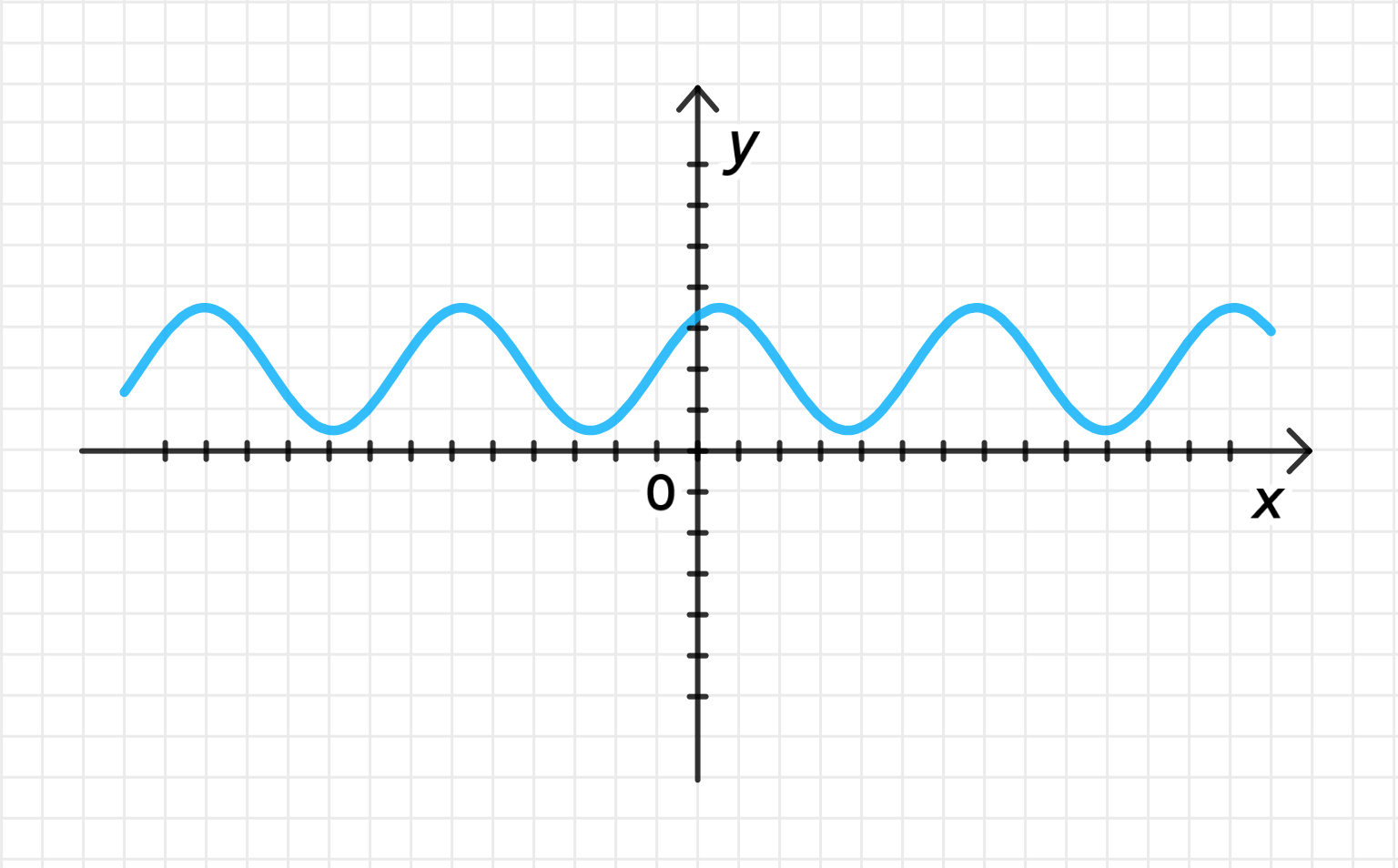
в) $y = -1,5 \sin \left( x — \frac{2\pi}{3} \right) + 2$;

Построим дугу графика $y = \sin x$, а затем:

• Переместим ее на $\frac{2\pi}{3}$ единиц вправо вдоль оси абсцисс;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 1,5$;
• Переместим ее на 2 единицы вверх вдоль оси ординат;

Достроим график функции:

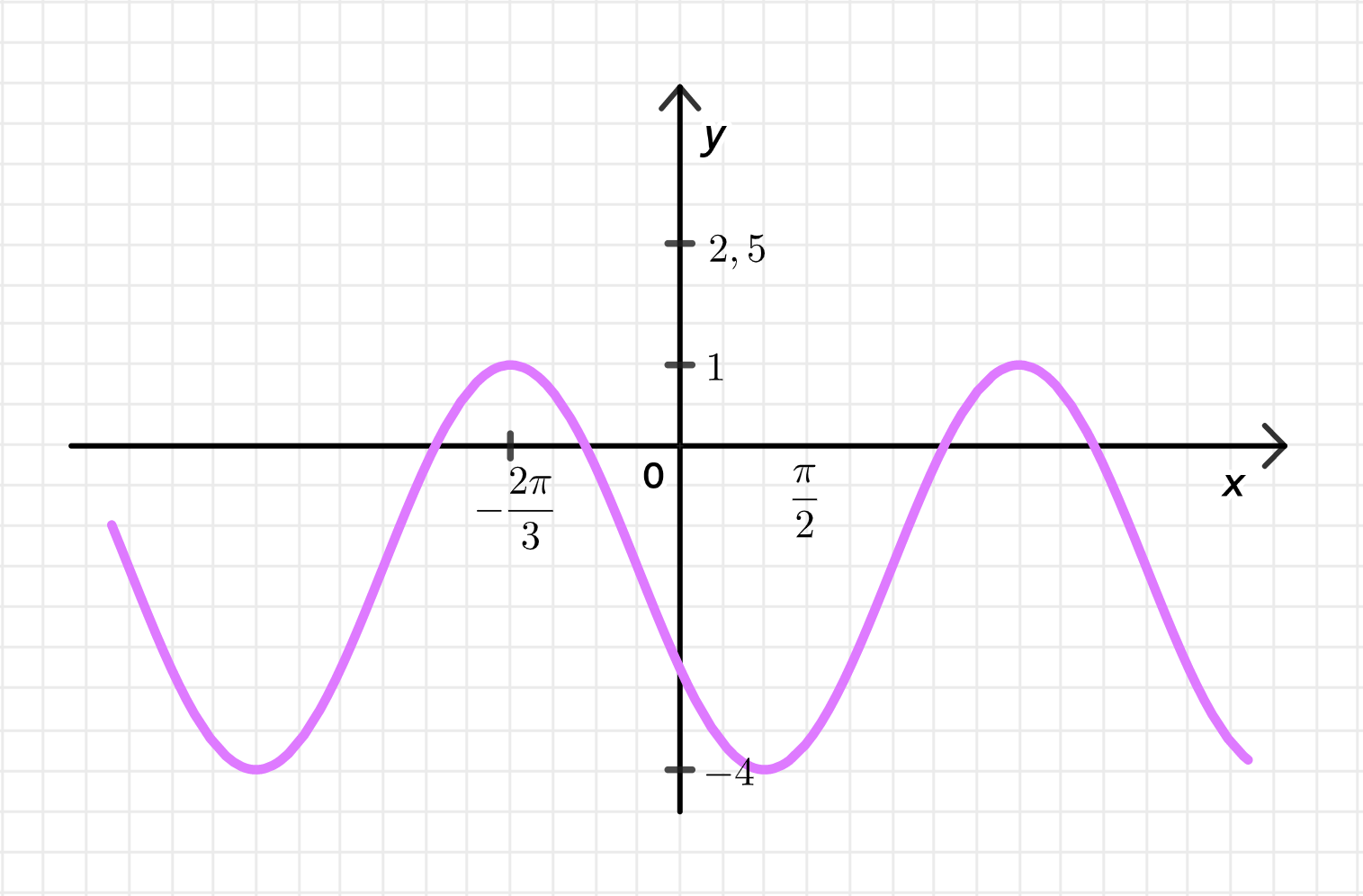
г) $y = 2,5 \cos \left( x + \frac{2\pi}{3} \right) — 1,5$;

Построим дугу графика $y = \cos x$, а затем:

• Переместим ее на $\frac{2\pi}{3}$ единиц влево вдоль оси абсцисс;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2,5$;
• Переместим ее на 1,5 единицы вниз вдоль оси ординат;

Достроим график функции:

а) $y = 2 \sin \left( x + \frac{\pi}{3} \right) + 1$

Шаг 1: Построение графика функции $y = \sin x$

График функции $y = \sin x$ — это стандартная синусоида, которая:

• Имеет период $T = 2\pi$,
• Колеблется между значениями $-1$ и $1$,
• Имеет амплитуду 1,
• Переходит через точку $(0, 0)$, достигает максимума в точке $x = \frac{\pi}{2}$, минимума в точке $x = \frac{3\pi}{2}$, и снова возвращается в точку $(2\pi, 0)$.

Рассмотрим несколько значений для функции $y = \sin x$:

Шаг 2: Перемещение графика на $\frac{\pi}{3}$ единиц влево вдоль оси абсцисс

Перемещаем график функции $y = \sin x$ на $\frac{\pi}{3}$ единиц влево. Это можно сделать, заменив $x$ на $x + \frac{\pi}{3}$. Такой сдвиг означает, что все значения $x$ на графике сдвигаются влево на $\frac{\pi}{3}$.

Для новых значений:

• Когда $x = -\frac{\pi}{3}$, $y = \sin \left( -\frac{\pi}{3} \right) = -\frac{\sqrt{3}}{2}$,
• Когда $x = 0$, $y = \sin(0) = 0$,
• Когда $x = \frac{\pi}{6}$, $y = \sin \left( \frac{\pi}{6} \right) = \frac{1}{2}$,
• Когда $x = \frac{\pi}{2}$, $y = \sin \left( \frac{\pi}{2} \right) = 1$,
• Когда $x = \frac{2\pi}{3}$, $y = \sin \left( \frac{2\pi}{3} \right) = \frac{\sqrt{3}}{2}$.

График теперь будет сдвинут на $\frac{\pi}{3}$ влево, и все его значения изменятся соответствующим образом.

Шаг 3: Растяжение графика по оси $y$ с коэффициентом $k = 2$

Теперь растягиваем график по оси $y$ с коэффициентом 2. Это означает, что все значения функции $y = \sin \left( x + \frac{\pi}{3} \right)$ умножаются на 2. Новый график будет $y = 2 \sin \left( x + \frac{\pi}{3} \right)$, и все значения $y$ будут колебаться между $-2$ и $2$.

• Когда $x = -\frac{\pi}{3}$, $y = 2 \times -\frac{\sqrt{3}}{2} = -\sqrt{3}$,
• Когда $x = 0$, $y = 2 \times 0 = 0$,
• Когда $x = \frac{\pi}{6}$, $y = 2 \times \frac{1}{2} = 1$,
• Когда $x = \frac{\pi}{2}$, $y = 2 \times 1 = 2$,
• Когда $x = \frac{2\pi}{3}$, $y = 2 \times \frac{\sqrt{3}}{2} = \sqrt{3}$.

Теперь амплитуда функции увеличена в 2 раза, и значения графика колеблются между $-2$ и $2$.

Шаг 4: Перемещение графика на 1 единицу вверх

Теперь перемещаем график функции на 1 единицу вверх. Для этого прибавляем 1 ко всем значениям функции. Получаем новую функцию:

$$y = 2 \sin \left( x + \frac{\pi}{3} \right) + 1$$

Теперь значения функции будут колебаться между $-1$ и $3$:

• Когда $x = -\frac{\pi}{3}$, $y = -\sqrt{3} + 1$,
• Когда $x = 0$, $y = 0 + 1 = 1$,
• Когда $x = \frac{\pi}{6}$, $y = 1 + 1 = 2$,
• Когда $x = \frac{\pi}{2}$, $y = 2 + 1 = 3$,
• Когда $x = \frac{2\pi}{3}$, $y = \sqrt{3} + 1$.

Шаг 5: Достроим график функции

б) $y = -3 \cos \left( x — \frac{5\pi}{6} \right) — 2$

Шаг 1: Построение графика функции $y = \cos x$

График функции $y = \cos x$ является стандартной косинусоидой:

• Период $T = 2\pi$,
• Колеблется между значениями $-1$ и $1$,
• Переходит через точку $(0, 1)$, достигает минимального значения в $x = \pi$, где $y = -1$.

Шаг 2: Перемещение графика на $\frac{5\pi}{6}$ единиц вправо вдоль оси абсцисс

Теперь перемещаем график функции $y = \cos x$ на $\frac{5\pi}{6}$ единиц вправо. Для этого заменяем $x$ на $x — \frac{5\pi}{6}$. График теперь начнется не с точки $(0, 1)$, а с точки $\left( \frac{5\pi}{6}, 1 \right)$.

Шаг 3: Отражение графика относительно оси абсцисс

Затем отражаем график относительно оси абсцисс, умножив все значения $y$ на -1. Это приведет к функции $y = -\cos \left( x — \frac{5\pi}{6} \right)$, которая будет располагаться ниже оси $x$.

Шаг 4: Растяжение графика по оси $y$ с коэффициентом $k = 3$

Теперь растягиваем график по оси $y$ с коэффициентом 3. Это означает, что все значения $y$ будут умножены на 3. Получаем функцию $y = -3 \cos \left( x — \frac{5\pi}{6} \right)$, которая будет колебаться между значениями $-3$ и $3$.

Шаг 5: Перемещение графика на 2 единицы вниз

Теперь сдвигаем график функции на 2 единицы вниз, вычитая 2 из всех значений $y$. Получаем новую функцию:

$$y = -3 \cos \left( x — \frac{5\pi}{6} \right) — 2$$

График будет колебаться между $-5$ и $1$.

Шаг 6: Достроим график функции

в) $y = -1,5 \sin \left( x — \frac{2\pi}{3} \right) + 2$

Шаг 1: Построение графика функции $y = \sin x$

График функции $y = \sin x$ уже рассмотрен. Он колеблется между значениями $-1$ и $1$.

Шаг 2: Перемещение графика на $\frac{2\pi}{3}$ единиц вправо вдоль оси абсцисс

Перемещаем график на $\frac{2\pi}{3}$ единиц вправо, заменив $x$ на $x — \frac{2\pi}{3}$. График теперь начнется в точке $\left( \frac{2\pi}{3}, 0 \right)$.

Шаг 3: Отражение графика относительно оси абсцисс

Отражаем график относительно оси абсцисс, умножив значения функции на -1. Теперь получаем график функции $y = -\sin \left( x — \frac{2\pi}{3} \right)$.

Шаг 4: Растяжение графика по оси $y$ с коэффициентом $k = 1,5$

Растягиваем график по оси $y$ с коэффициентом $k = 1,5$. Функция будет $y = -1,5 \sin \left( x — \frac{2\pi}{3} \right)$.

Шаг 5: Перемещение графика на 2 единицы вверх

Теперь сдвигаем график на 2 единицы вверх, прибавив 2 ко всем значениям функции. Получаем:

$$y = -1,5 \sin \left( x — \frac{2\pi}{3} \right) + 2$$

Шаг 6: Достроим график функции

г) $y = 2,5 \cos \left( x + \frac{2\pi}{3} \right) — 1,5$

Шаг 1: Построение графика функции $y = \cos x$

График функции $y = \cos x$ был рассмотрен ранее. Он колеблется между $-1$ и $1$.

Шаг 2: Перемещение графика на $\frac{2\pi}{3}$ единиц влево

Перемещаем график на $\frac{2\pi}{3}$ единиц влево, заменив $x$ на $x + \frac{2\pi}{3}$.

Шаг 3: Отражение графика относительно оси абсцисс

Отражаем график относительно оси абсцисс, получаем функцию $y = -\cos \left( x + \frac{2\pi}{3} \right)$.

Шаг 4: Растяжение графика по оси $y$ с коэффициентом $k = 2,5$

Растягиваем график по оси $y$ с коэффициентом 2,5. Получаем функцию $y = 2,5 \cos \left( x + \frac{2\pi}{3} \right)$.

Шаг 5: Перемещение графика на 1,5 единицы вниз

Теперь сдвигаем график на 1,5 единицы вниз:

$$y = 2,5 \cos \left( x + \frac{2\pi}{3} \right) — 1,5$$

Шаг 6: Достроим график функции