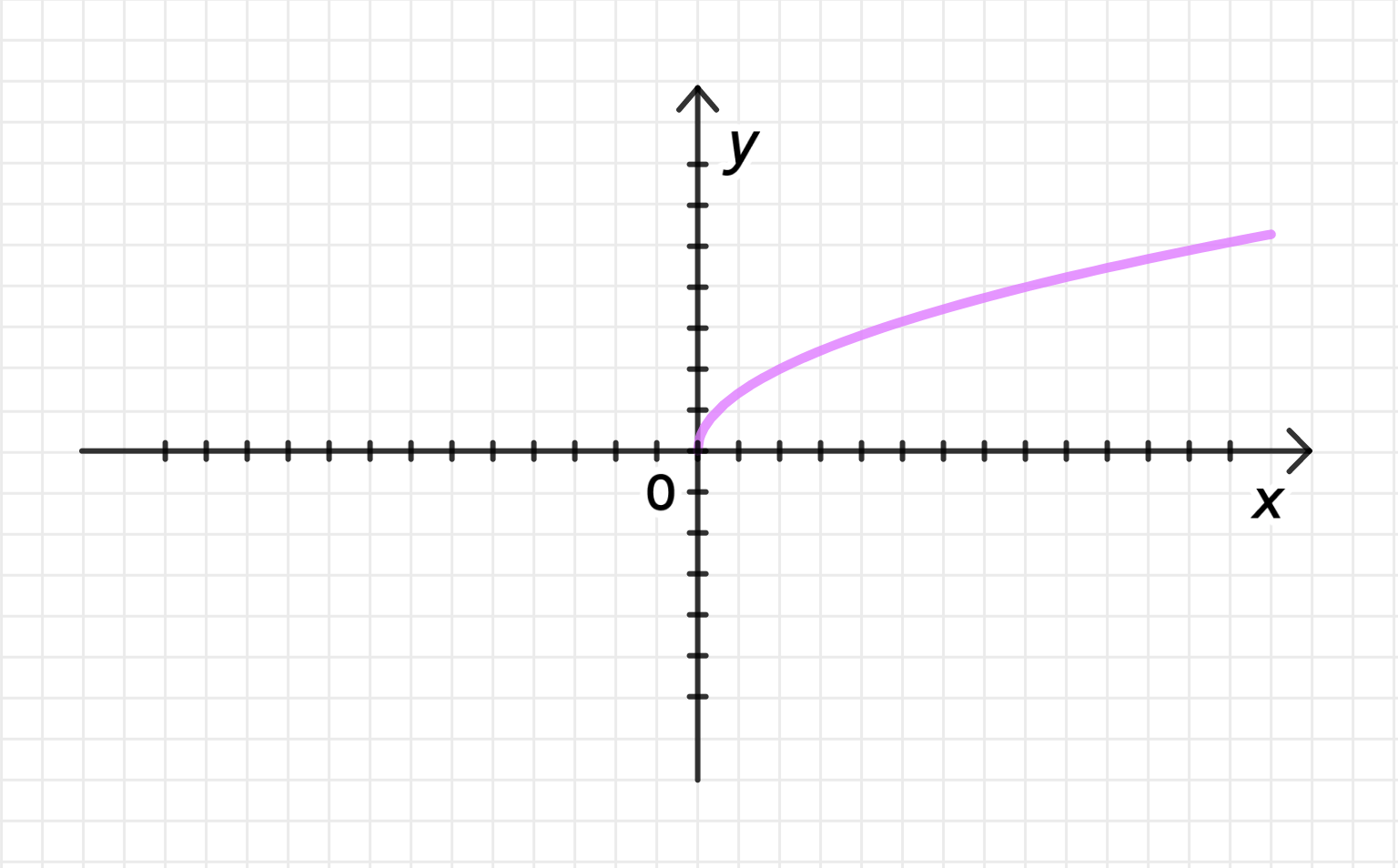Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 18.1 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а) ;
б) ;
в) ;
г)
а) ;
Построим график функции :
| 0 | 1 | 4 | 9 | 16 | |
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 |
Совершим сжатие графика к оси с коэффициентом .
б) ;
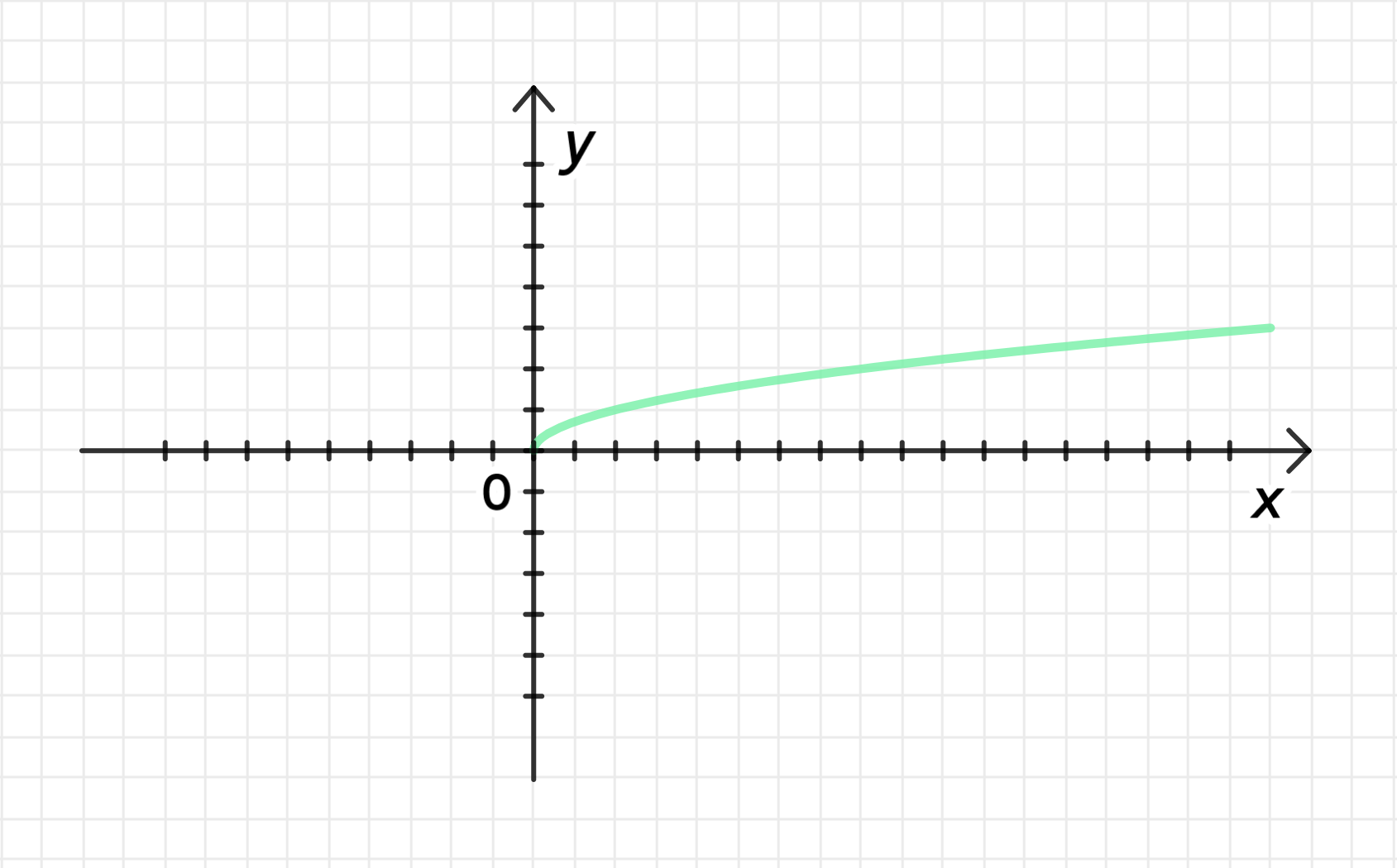
Построим график функции :
| 0 | 1 | 4 | 9 | |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 |
Совершим растяжение графика от оси с коэффициентом .
в) ;
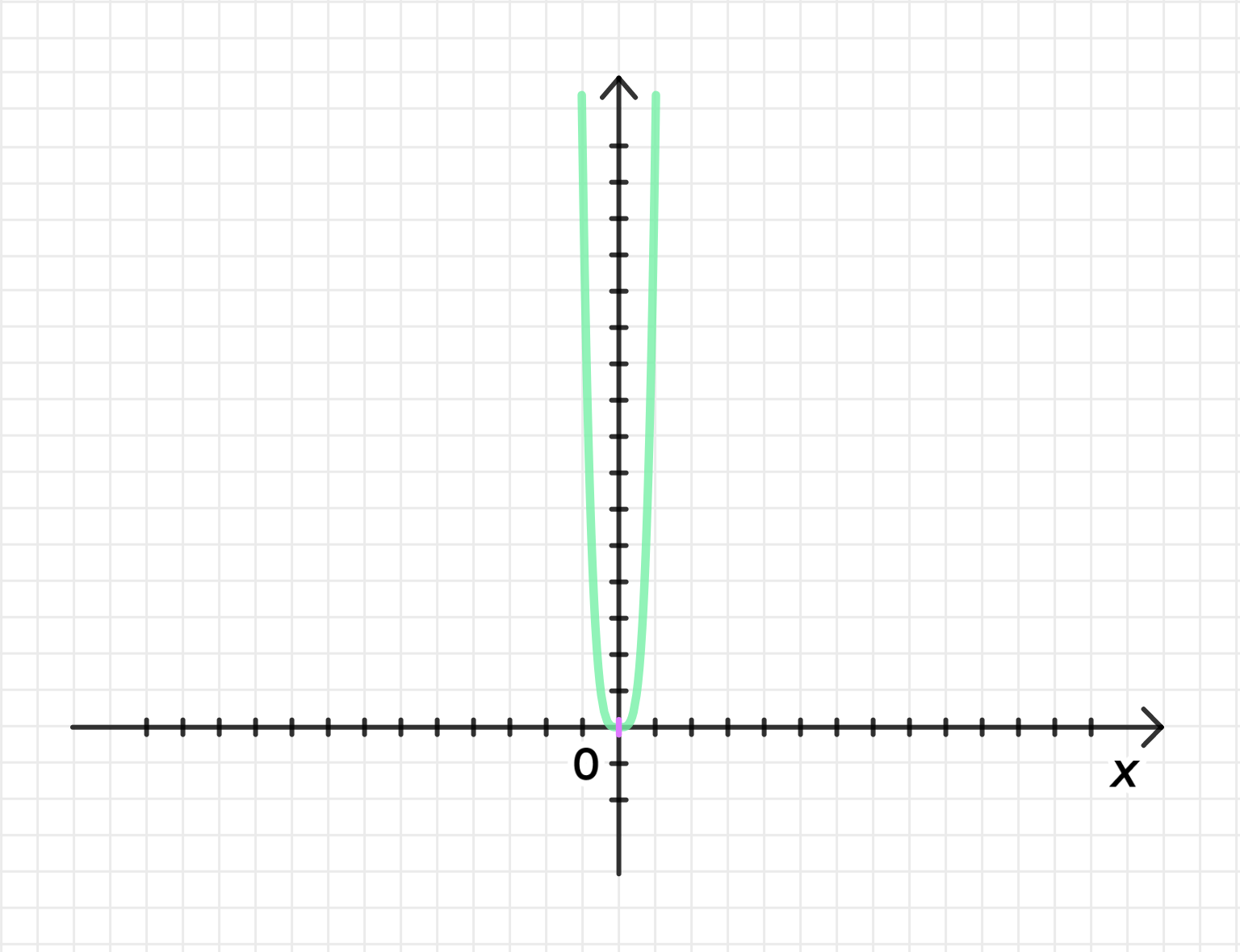
Построим график функции :
| -2 | -1 | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| 16 | 1 | 0 | 1 | 16 |
Совершим сжатие графика к оси с коэффициентом .
г) ;
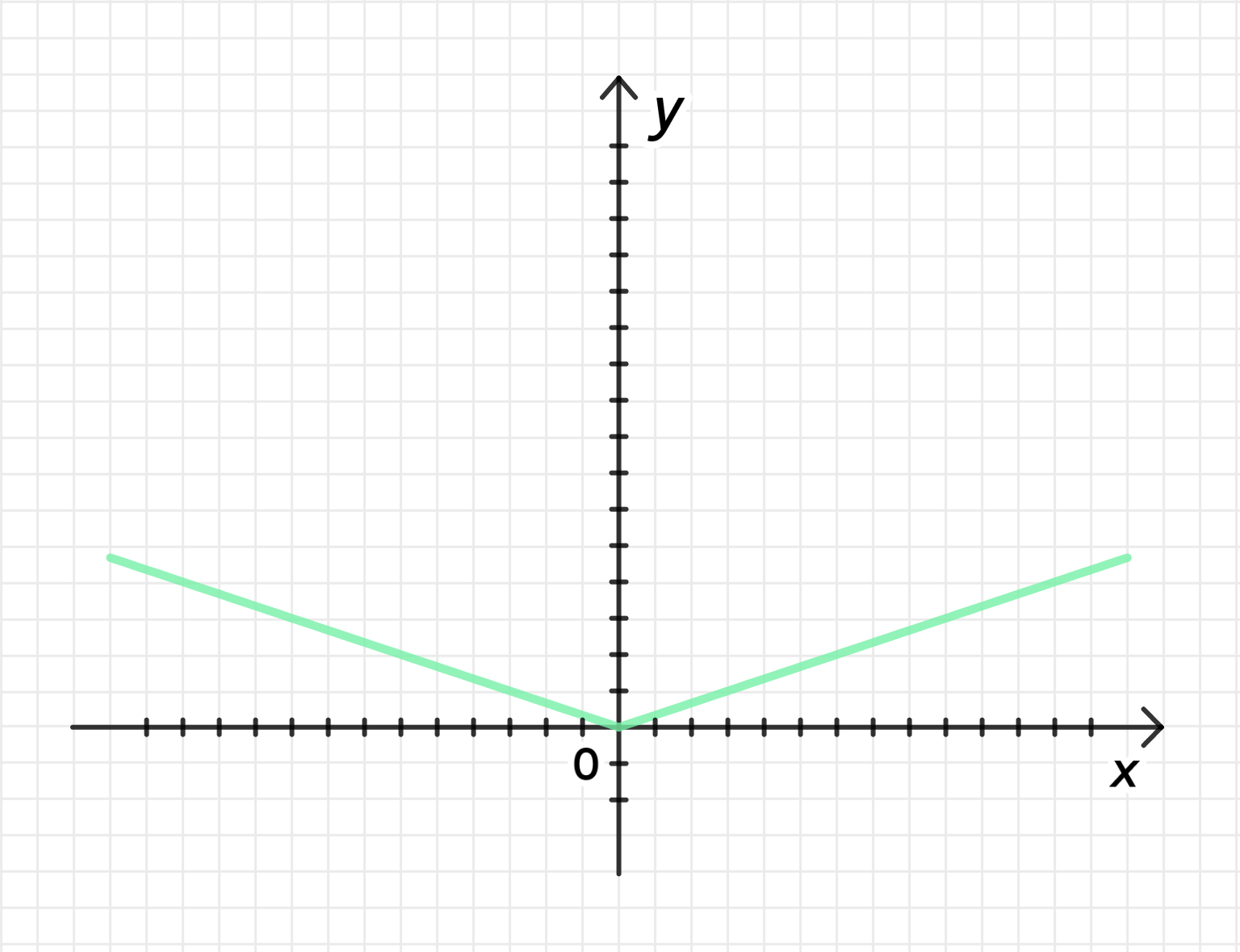
Построим график функции :
| -1 | 0 | 1 | |
|---|---|---|---|
| 1 | 0 | 1 |
Совершим растяжение графика от оси с коэффициентом .
а)
1) Построение графика функции
Для начала рассмотрим график функции , которая является стандартной корневой функцией.
- Для : .
- Для : .
- Для : .
- Для : .
- Для : .
Получаем таблицу значений:
| 0 | 1 | 4 | 9 | 16 | |
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 |
График этой функции будет выглядеть как плавно возрастающая кривая, начинающаяся от начала координат и стремящаяся к бесконечности по мере увеличения . График функции всегда лежит в первой и второй четверти, так как для отрицательных значений она не определена.
2) Совершим сжатие графика к оси с коэффициентом
Функция отличается от тем, что в её аргументе присутствует множитель 2. Это вызовет сжатие графика вдоль оси , что эквивалентно растяжению вдоль оси на коэффициент .
Чтобы это понять, нужно провести замену: при для любого мы получаем . Это означает, что для того, чтобы получить то же самое значение , нужно в два раза уменьшить, то есть растягивается в два раза в сравнении с графиком функции .
Таким образом, график функции будет «сжат» вдоль оси , и его значения для всех будут в два раза меньше, чем значения на графике .
б)
1) Построение графика функции
Сначала построим график функции , как и в предыдущем примере.
- Для : .
- Для : .
- Для : .
- Для : .
Таблица значений:
| 0 | 1 | 4 | 9 | |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 |
График функции будет тем же, что и в примере выше.
2) Совершим растяжение графика от оси с коэффициентом
Теперь рассмотрим функцию . Эта функция отличается от тем, что в аргументе синуса присутствует деление на 2. Это означает, что график будет растянут вдоль оси .
Чтобы понять это, вспомним, что если у нас есть функция вида , где , то график будет сжаться вдоль оси , а если , то график будет растягиваться.
В нашем случае , то есть график будет растягиваться по оси на коэффициент , так как вместо на графике будет иметься , что увеличивает значения функции для каждого .
в)
1) Построение графика функции
Рассмотрим стандартную функцию . Значения для будут следующие:
- Для : .
- Для : .
- Для : .
- Для : .
- Для : .
Таблица значений:
| -2 | -1 | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| 16 | 1 | 0 | 1 | 16 |
График функции будет симметричен относительно оси (поскольку функция четная), и будет иметь «вытянутую» форму, стремящуюся к бесконечности как при , так и при .
2) Совершим сжатие графика к оси с коэффициентом
Теперь рассматриваем функцию . Заметим, что для каждого , функция , что означает увеличение всех значений функции в 16 раз.
Однако, по сравнению с , происходит сжатие вдоль оси , так как множитель в выражении внутри скобок увеличивает амплитуду функции.
Таким образом, график функции будет сжат вдоль оси с коэффициентом , то есть для каждого значения , функция будет более «плоской», чем .
г)
1) Построение графика функции
Рассмотрим стандартную функцию , которая представляет собой «V»-образную фигуру:
- Для : .
- Для : .
- Для : .
Таблица значений:
| -1 | 0 | 1 | |
|---|---|---|---|
| 1 | 0 | 1 |
График функции будет «V»-образной линией, с вершиной в точке , и с угловым коэффициентом, равным 1.
2) Совершим растяжение графика от оси с коэффициентом
Теперь рассматриваем функцию . Это выражение является растяжением функции вдоль оси , так как мы делим на 3. Это растягивает график вдоль оси .
Для каждой точки , значение функции будет в 3 раза больше, чем на графике , так как теперь в каждой точке будет большее значение функции.
Таким образом, график функции будет растянут вдоль оси с коэффициентом .