ГДЗ по Алгебре 10 Класс Номер 18.15 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

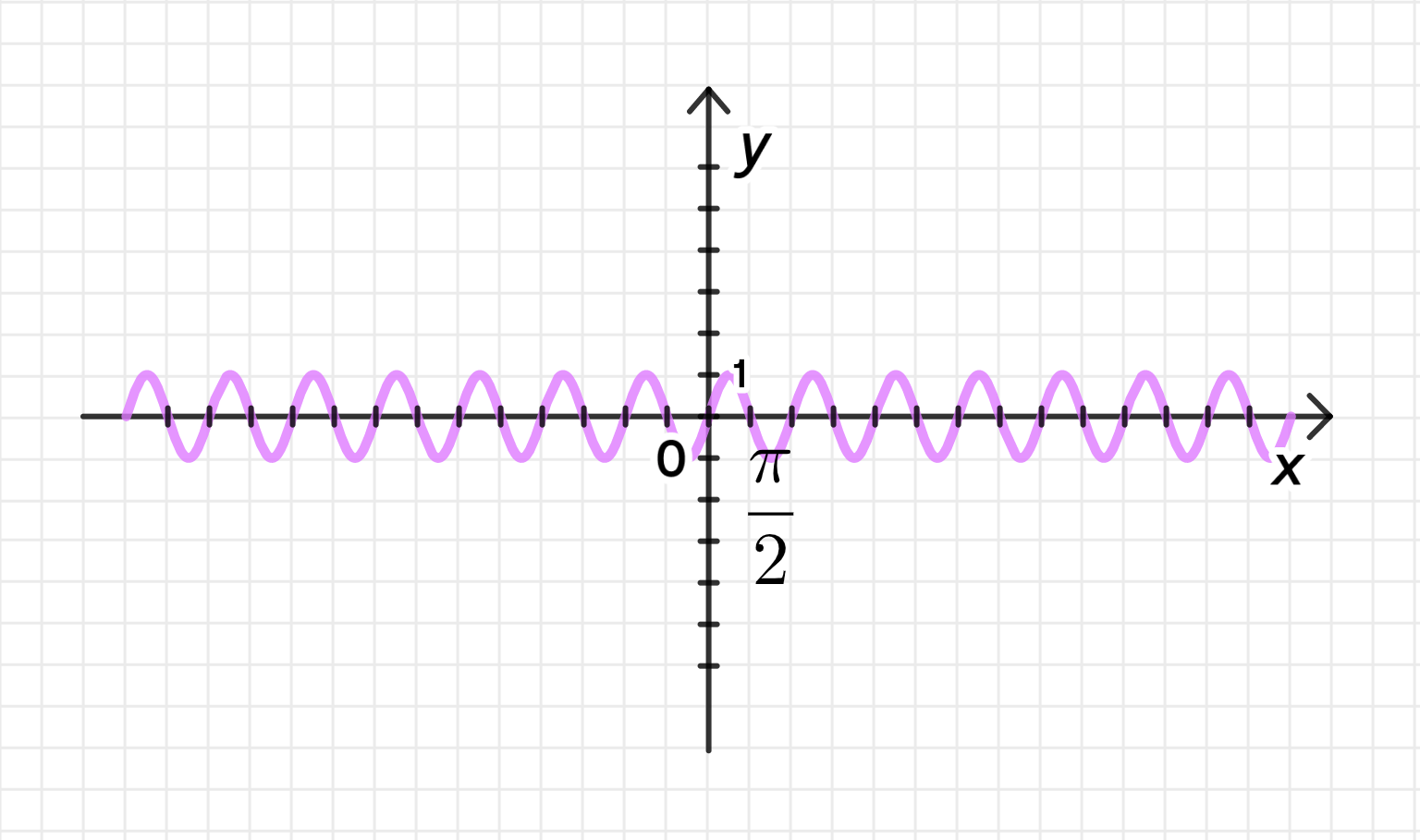
а) $y = \sin \pi x$;

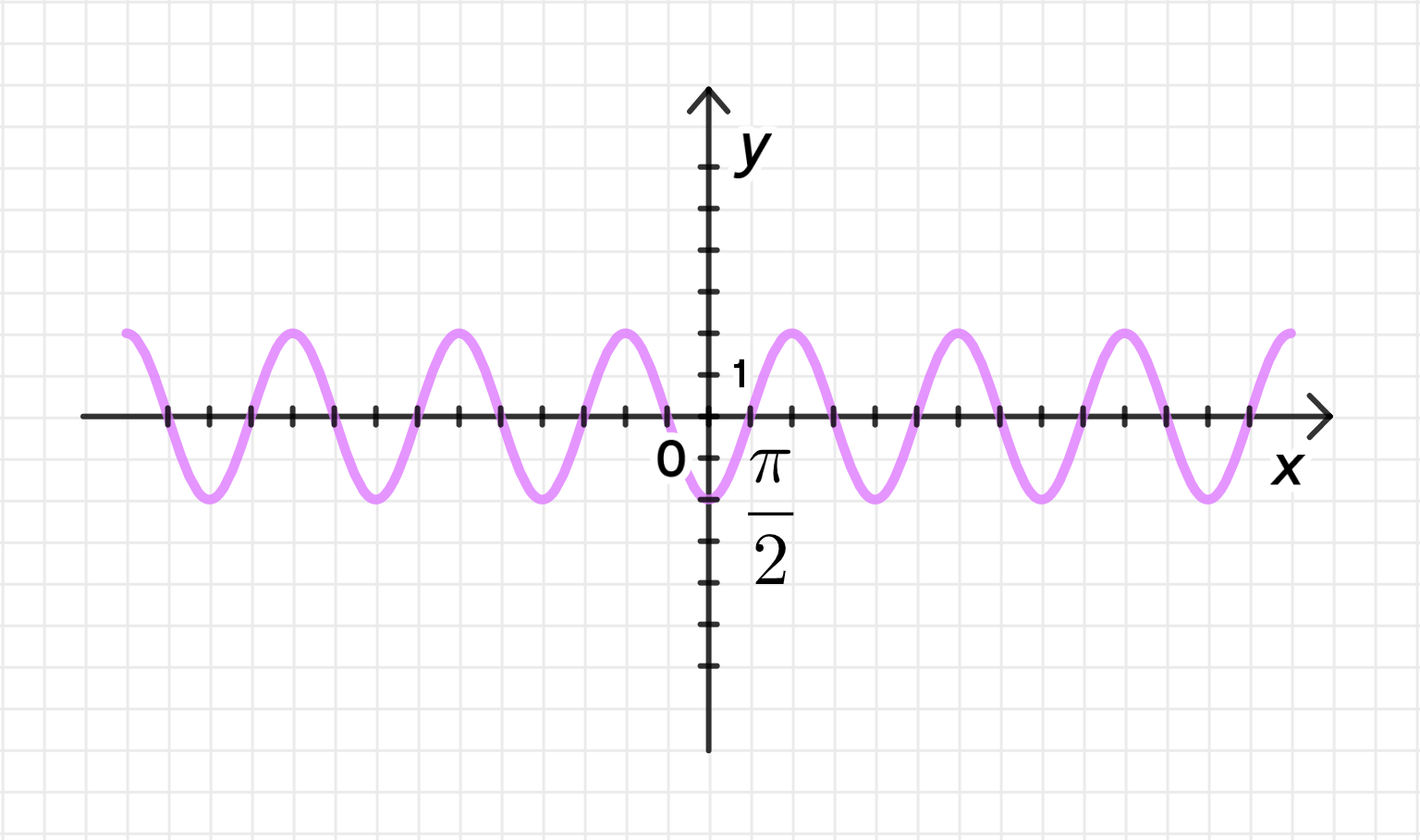
$$y(1) = \sin \pi = 0;$$б) $y = -2 \cos \frac{\pi x}{2}$;

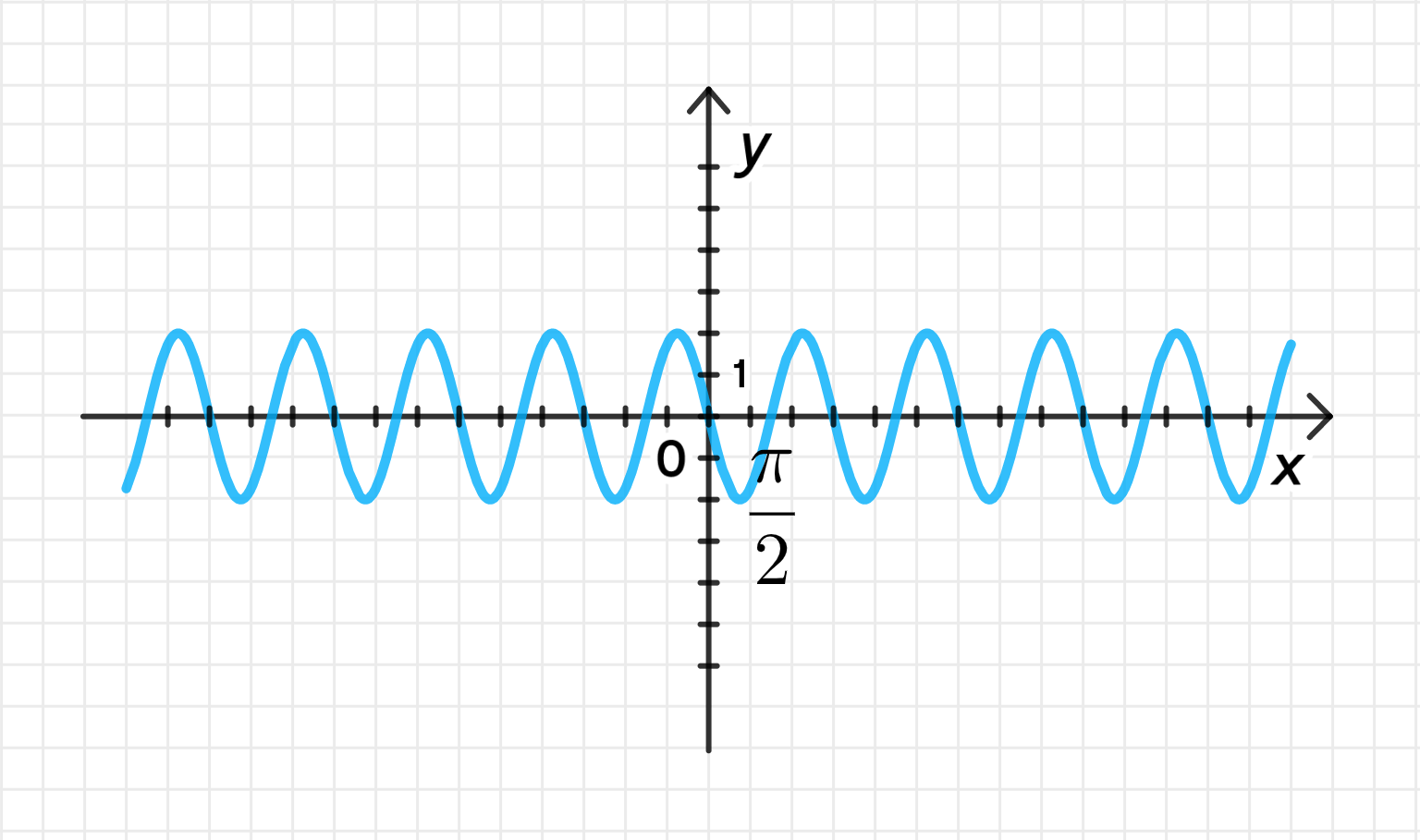
в) $y = -2 \sin \frac{2\pi x}{3}$;

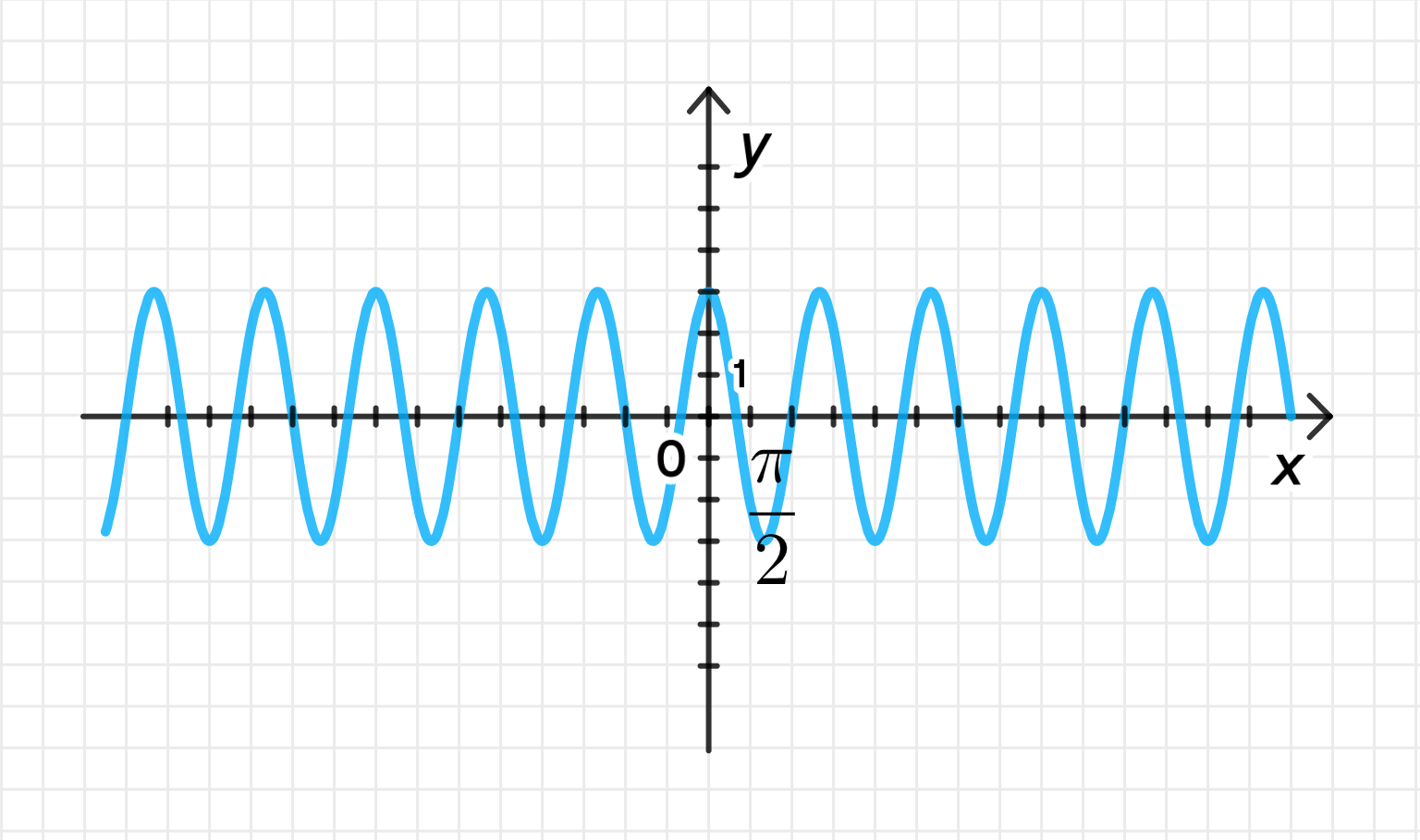
г) $y = 3 \cos \frac{3\pi x}{4}$

а) $y = \sin \pi x$;

Первая дуга лежит на отрезке:

$$0 \leq x \leq \pi;$$ $$0 \leq x \leq \frac{\pi}{\pi};$$ $$0 \leq x \leq 1;$$

Построим дугу синусоиды:

$$y(0) = \sin(\pi \cdot 0) = \sin 0 = 0;$$ $$y(0.5) = \sin \frac{\pi}{2} = 1;$$ $$y(1) = \sin \pi = 0;$$

Достроим график функции:

б) $y = -2 \cos \frac{\pi x}{2}$;

Первая дуга лежит на отрезке:

$$-\frac{\pi}{2} \leq x \leq \frac{\pi}{2};$$ $$-\frac{\pi}{2} \cdot \frac{2}{\pi} \leq x \leq \frac{\pi}{2} \cdot \frac{2}{\pi};$$ $$-1 \leq x \leq 1;$$

Построим дугу синусоиды:

$$y(\pm 1) = -2 \cos \left( \frac{\pi}{2} \right) = -2 \cdot 0 = 0;$$ $$y(0) = -2 \cos \left( \frac{\pi}{2} \cdot 0 \right) = -2 \cos 0 = -2 \cdot 1 = -2;$$

Достроим график функции:

в) $y = -2 \sin \frac{2\pi x}{3}$;

Первая дуга лежит на отрезке:

$$0 \leq x \leq \pi;$$ $$0 \cdot \frac{3}{2\pi} \leq x \leq \pi \cdot \frac{3}{2\pi};$$ $$0 \leq x \leq \frac{3}{2};$$

Построим дугу синусоиды:

$$y(0) = -2 \sin \left( \frac{2\pi}{3} \cdot 0 \right) = -2 \sin 0 = -2 \cdot 0 = 0;$$ $$y(0.75) = -2 \sin \left( \frac{2\pi}{3} \cdot \frac{3}{4} \right) = -2 \sin \frac{\pi}{2} = -2 \cdot 1 = -2;$$ $$y(1.5) = -2 \sin \left( \frac{2\pi}{3} \cdot \frac{3}{2} \right) = -2 \sin \pi = -2 \cdot 0 = 0;$$

Достроим график функции:

г) $y = 3 \cos \frac{3\pi x}{4}$;

Первая дуга лежит на отрезке:

$$-\frac{\pi}{2} \leq x \leq \frac{\pi}{2};$$ $$-\frac{\pi}{2} \cdot \frac{4}{3\pi} \leq x \leq \frac{\pi}{2} \cdot \frac{4}{3\pi};$$ $$-\frac{2}{3} \leq x \leq \frac{2}{3};$$

Построим дугу синусоиды:

$$y \left( \pm \frac{2}{3} \right) = 3 \cos \left( \frac{3\pi}{4} \cdot \frac{2}{3} \right) = 3 \cos \frac{\pi}{2} = 3 \cdot 0 = 0;$$ $$y(0) = 3 \cos \left( \frac{3\pi}{4} \cdot 0 \right) = 3 \cos 0 = 3 \cdot 1 = 3;$$

Достроим график функции:

а) $y = \sin \pi x$

Шаг 1: Анализ функции

Общий вид функции:
Функция $y = \sin \pi x$ — это стандартная синусоида, но с коэффициентом $\pi$ перед переменной $x$. Это влияет на период функции.

Период:
Период функции $y = \sin kx$ вычисляется по формуле:

$$T = \frac{2\pi}{|k|}.$$

Для нашей функции $k = \pi$, поэтому период будет равен:

$$T = \frac{2\pi}{\pi} = 2.$$

Это означает, что функция будет повторяться каждые 2 единицы по оси $x$.

Шаг 2: Исследование графика

Первая дуга:
Первая дуга функции начинается при $x = 0$ и заканчивается на $x = 1$, так как $y = \sin \pi x$ делает полный цикл на интервале от 0 до 2. Таким образом, первая дуга будет лежать на отрезке $0 \leq x \leq 1$.

Построение значений на ключевых точках:
Для того чтобы построить график функции, вычислим её значения в ключевых точках:

• $y(0) = \sin(\pi \cdot 0) = \sin(0) = 0$,
• $y(0.5) = \sin \left( \pi \cdot 0.5 \right) = \sin \left( \frac{\pi}{2} \right) = 1$,
• $y(1) = \sin(\pi \cdot 1) = \sin(\pi) = 0$.

Таким образом, функция начинается в точке $(0, 0)$, достигает максимума в точке $(0.5, 1)$, и возвращается в точку $(1, 0)$.

График функции:

б) $y = -2 \cos \frac{\pi x}{2}$

Шаг 1: Анализ функции

Общий вид функции:
Функция $y = -2 \cos \frac{\pi x}{2}$ — это косинусоида с двумя трансформациями:

• Множитель $-2$ влияет на амплитуду функции, растягивая её по вертикали и меняя знак.
• Аргумент $\frac{\pi x}{2}$ изменяет период функции.

Период:
Период функции $y = \cos(kx)$ вычисляется по формуле:

$$T = \frac{2\pi}{|k|}.$$

Здесь $k = \frac{\pi}{2}$, поэтому период будет равен:

$$T = \frac{2\pi}{\frac{\pi}{2}} = 4.$$

Таким образом, период функции равен 4, то есть она будет повторяться каждые 4 единицы по оси $x$.

Шаг 2: Исследование графика

Первая дуга:
Первая дуга функции будет лежать на отрезке $-1 \leq x \leq 1$, поскольку косинусоида с таким периодом пройдёт один полный цикл именно на этом промежутке.

Построение значений на ключевых точках:
Вычислим значения функции в ключевых точках:

• $y(\pm 1) = -2 \cos \left( \frac{\pi}{2} \right) = -2 \cdot 0 = 0$,
• $y(0) = -2 \cos \left( \frac{\pi}{2} \cdot 0 \right) = -2 \cdot 1 = -2$.

Таким образом, функция начинается в точке $(0, -2)$, проходит через точки $(-1, 0)$ и $(1, 0)$.

График функции:

в) $y = -2 \sin \frac{2\pi x}{3}$

Шаг 1: Анализ функции

Общий вид функции:
Функция $y = -2 \sin \frac{2\pi x}{3}$ — это синусоида с двумя трансформациями:

• Множитель $-2$ меняет амплитуду функции и инвертирует её по вертикали.
• Аргумент $\frac{2\pi x}{3}$ влияет на период функции.

Период:
Период функции $y = \sin(kx)$ вычисляется по формуле:

$$T = \frac{2\pi}{|k|}.$$

Здесь $k = \frac{2\pi}{3}$, поэтому период будет равен:

$$T = \frac{2\pi}{\frac{2\pi}{3}} = 3.$$

Период функции равен 3, то есть функция будет повторяться каждые 3 единицы по оси $x$.

Шаг 2: Исследование графика

Первая дуга:
Первая дуга функции будет лежать на отрезке $0 \leq x \leq 1.5$, так как на этом промежутке синусоида проходит половину своего цикла.

Построение значений на ключевых точках:
Вычислим значения функции в ключевых точках:

• $y(0) = -2 \sin \left( \frac{2\pi}{3} \cdot 0 \right) = -2 \sin 0 = 0$,
• $y(0.75) = -2 \sin \left( \frac{2\pi}{3} \cdot \frac{3}{4} \right) = -2 \sin \frac{\pi}{2} = -2 \cdot 1 = -2$,
• $y(1.5) = -2 \sin \left( \frac{2\pi}{3} \cdot \frac{3}{2} \right) = -2 \sin \pi = 0$.

Таким образом, функция начинается в точке $(0, 0)$, достигает минимального значения $-2$ в точке $(0.75, -2)$, и возвращается в точку $(1.5, 0)$.

График функции:

г) $y = 3 \cos \frac{3\pi x}{4}$

Шаг 1: Анализ функции

Общий вид функции:
Функция $y = 3 \cos \frac{3\pi x}{4}$ — это косинусоида с двумя трансформациями:

• Множитель $3$ увеличивает амплитуду функции.
• Аргумент $\frac{3\pi x}{4}$ изменяет период функции.

Период:
Период функции $y = \cos(kx)$ вычисляется по формуле:

$$T = \frac{2\pi}{|k|}.$$

Здесь $k = \frac{3\pi}{4}$, поэтому период будет равен:

$$T = \frac{2\pi}{\frac{3\pi}{4}} = \frac{8}{3}.$$

Период функции равен $\frac{8}{3}$, то есть функция будет повторяться каждые $\frac{8}{3}$ единиц по оси $x$.

Шаг 2: Исследование графика

Первая дуга:
Первая дуга функции будет лежать на отрезке $-\frac{2}{3} \leq x \leq \frac{2}{3}$, так как на этом промежутке функция делает полный цикл.

Построение значений на ключевых точках:
Вычислим значения функции в ключевых точках:

• $y \left( \pm \frac{2}{3} \right) = 3 \cos \left( \frac{3\pi}{4} \cdot \frac{2}{3} \right) = 3 \cos \frac{\pi}{2} = 0$,
• $y(0) = 3 \cos \left( \frac{3\pi}{4} \cdot 0 \right) = 3 \cos 0 = 3$.

Таким образом, функция начинается в точке $(0, 3)$, проходит через точки $\left( -\frac{2}{3}, 0 \right)$ и $\left( \frac{2}{3}, 0 \right)$.

График функции: