ГДЗ по Алгебре 10 Класс Номер 18.16 Профильный Уровень Мордкович — Подробные Ответы

а) $y=\frac{1}{2}\cos 3(x-\frac{\pi }{3})$

б) $y=-1,5\sin \frac{2}{3}(x+\frac{\pi }{2})$$$$$

а) $y = \frac{1}{2} \cos 3 \left( x — \frac{\pi}{3} \right) = \frac{1}{2} \cos (3x — \pi)$;

Построим дугу графика $y = \cos x$, а затем:

• Переместим ее на $\pi$ единиц вправо вдоль оси абсцисс;
• Совершим ее сжатие к оси $Oy$ с коэффициентом $k = 3$;
• Совершим ее сжатие к оси $Ox$ с коэффициентом $k = 2$;

Достроим график функции:

б) $y = -1,5 \sin \frac{2}{3} \left( x + \frac{\pi}{2} \right) = -1,5 \sin \left( \frac{2}{3} x + \frac{\pi}{3} \right)$;

Построим дугу графика $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{3}$ единиц влево вдоль оси абсцисс;
• Совершим ее растяжение от оси $Oy$ с коэффициентом $k = 1,5$;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 1,5$;

Достроим график функции:

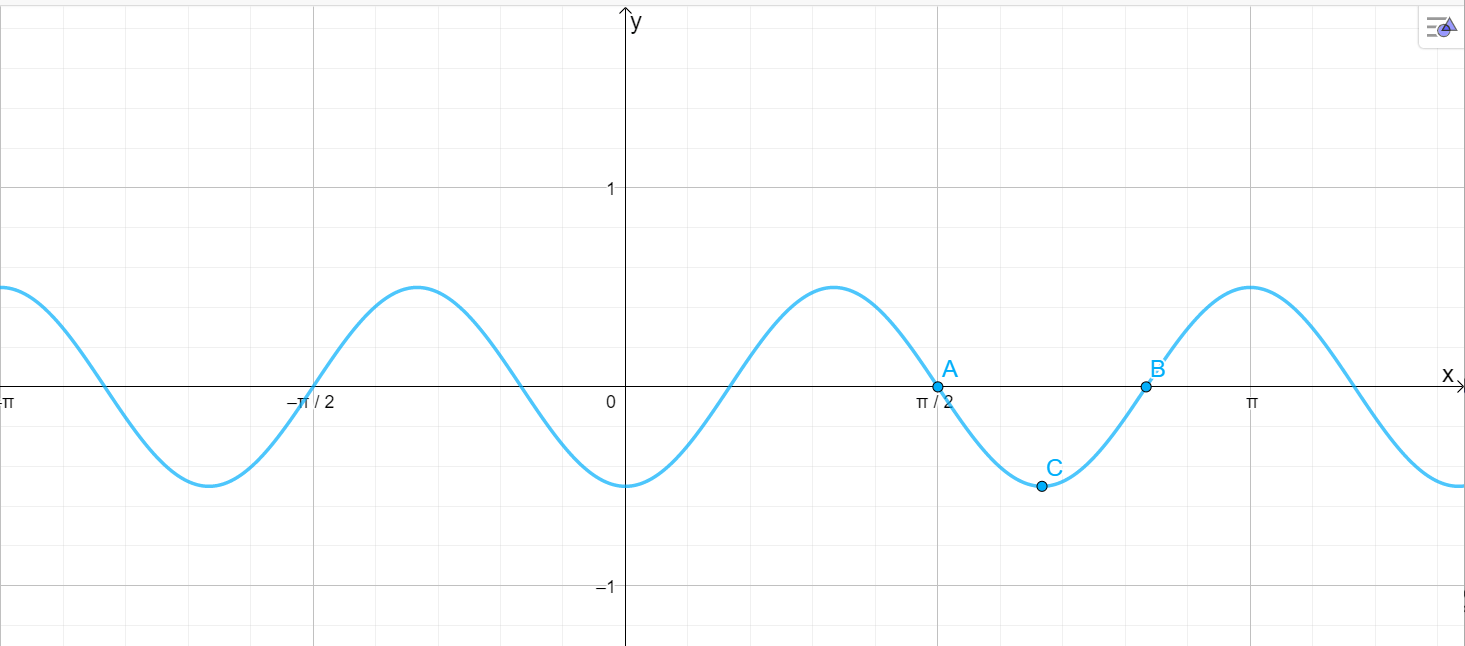
а) $y = \frac{1}{2} \cos 3 \left( x — \frac{\pi}{3} \right) = \frac{1}{2} \cos (3x — \pi)$

Мы ищем график функции, полученной из стандартной функции $y = \cos x$ с рядом преобразований. Важно выделить, какие конкретно преобразования происходят с графиком, исходя из выражения $y = \frac{1}{2} \cos (3x — \pi)$. Преобразования описываются следующими шагами:

1) Построим дугу графика $y = \cos x$:

График функции $y = \cos x$ — это стандартная косинусоида, которая:

• Имеет амплитуду 1, то есть колеблется от -1 до 1.
• Имеет период $2\pi$, то есть она повторяется через $2\pi$.
• Пересекает ось $Ox$ в точках $x = \frac{\pi}{2}, \frac{3\pi}{2}, \dots$.
• Пересекает ось $Oy$ в точке $x = 0$.

Теперь рассмотрим, как видоизменяется этот график.

2) Перемещаем график на $\pi$ единиц вправо вдоль оси абсцисс:

Мы видим, что выражение в скобках $\left( x — \frac{\pi}{3} \right)$ указывает на сдвиг графика вправо на $\frac{\pi}{3}$. Однако, после приведения этого выражения к виду $3x — \pi$, можно говорить о сдвиге вправо на $\frac{\pi}{3}$, что соответствует сдвигу графика вправо.

3) Совершаем сжатие графика вдоль оси $Oy$ с коэффициентом $k = 3$:

Перед коэффициентом $\cos x$ стоит множитель $\frac{1}{2}$. Это означает, что весь график сжимается вдоль оси $Oy$, то есть амплитуда косинусоиды уменьшается с 1 до $\frac{1}{2}$.

4) Совершаем сжатие графика вдоль оси $Ox$ с коэффициентом $k = 2$:

В выражении $\cos (3x — \pi)$ перед $x$ стоит множитель 3. Это означает, что график сжимается вдоль оси $Ox$ в 3 раза, что приводит к сокращению периода функции. Период функции $y = \cos x$ равен $2\pi$, а для графика функции с коэффициентом 3 в аргументе период будет $\frac{2\pi}{3}$.

5) Достроим график функции:

В результате этих преобразований получим график функции $y = \frac{1}{2} \cos (3x — \pi)$. Он будет иметь следующие характеристики:

• Амплитуда $\frac{1}{2}$.
• Период $\frac{2\pi}{3}$.
• Сдвиг вправо на $\frac{\pi}{3}$.
• Сжатие вдоль оси $Oy$ и оси $Ox$.

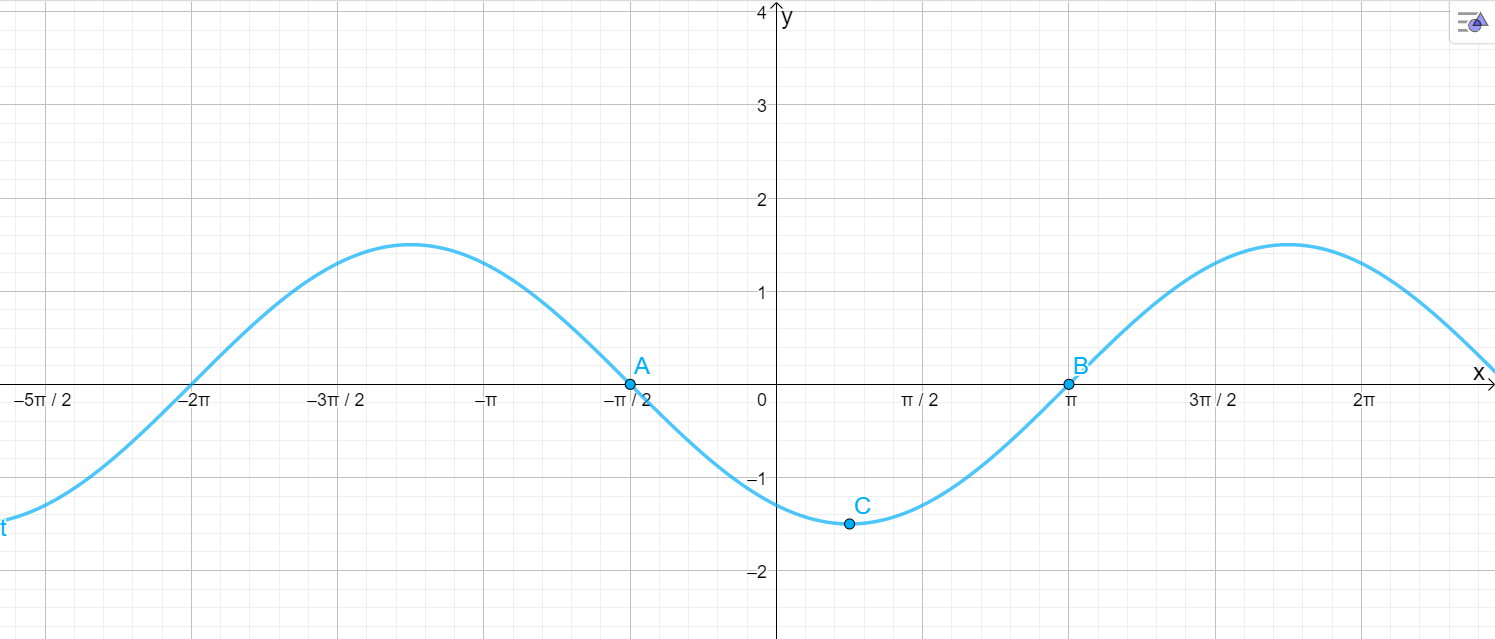
б) $y = -1,5 \sin \frac{2}{3} \left( x + \frac{\pi}{2} \right) = -1,5 \sin \left( \frac{2}{3} x + \frac{\pi}{3} \right)$

Теперь рассмотрим график функции $y = -1,5 \sin \frac{2}{3} \left( x + \frac{\pi}{2} \right)$. Мы снова будем рассматривать преобразования стандартного графика функции $y = \sin x$.

1) Построим дугу графика $y = \sin x$:

График функции $y = \sin x$ — это стандартная синусоида, которая:

• Имеет амплитуду 1.
• Имеет период $2\pi$.
• Пересекает ось $Ox$ в точках $x = 0, \pi, 2\pi, \dots$.
• Пересекает ось $Oy$ в точке $x = 0$.

2) Перемещаем график на $\frac{\pi}{3}$ единиц влево вдоль оси абсцисс:

В выражении $\sin \left( \frac{2}{3} x + \frac{\pi}{3} \right)$ присутствует сдвиг на $-\frac{\pi}{3}$ по оси $x$, что означает перемещение графика на $\frac{\pi}{3}$ влево.

3) Совершаем растяжение графика вдоль оси $Oy$ с коэффициентом $k = 1,5$:

Перед синусом стоит множитель $-1,5$. Это означает, что график будет растягиваться вдоль оси $Oy$ с коэффициентом 1,5, а также изменится знак, так как множитель отрицательный. Следовательно, график будет перевернут относительно оси $Ox$, и его амплитуда станет 1,5.

4) Совершаем растяжение графика вдоль оси $Ox$ с коэффициентом $k = 1,5$:

Коэффициент $\frac{2}{3}$ перед $x$ приводит к растяжению графика по оси $x$. Период функции изменится, и новый период будет равен $\frac{2\pi}{\frac{2}{3}} = 3\pi$.

5) Достроим график функции:

Таким образом, график функции $y = -1,5 \sin \frac{2}{3} (x + \frac{\pi}{2})$ будет иметь следующие характеристики:

• Амплитуда 1,5, и она будет направлена вниз (из-за минусового знака перед множителем).
• Период $3\pi$.
• Сдвиг влево на $\frac{\pi}{3}$.