ГДЗ по Алгебре 10 Класс Номер 18.17 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \sin(x + |x|);$

б) $y = \cos\frac{x — 2|x|}{2};$

в) $y = \cos(x + |x|);$

г) $y=\sin \frac{x+3\mathrm{\mid }x\mathrm{\mid }}{2}$

а) $y = \sin(x + |x|);$

Если $x \geq 0$, тогда:

$$y = \sin(x + x) = \sin 2x;$$

Если $x < 0$, тогда:

$$y = \sin(x — x) = \sin 0 = 0;$$

График функции:

б) $y = \cos\frac{x — 2|x|}{2};$

Если $x \geq 0$, тогда:

$$y = \cos\frac{x — 2x}{2} = \cos\left(-\frac{x}{2}\right) = \cos\frac{x}{2};$$

Если $x < 0$, тогда:

$$y = \cos\frac{x + 2x}{2} = \cos\frac{3x}{2};$$

График функции:

в) $y = \cos(x + |x|);$

Если $x \geq 0$, тогда:

$$y = \cos(x + x) = \cos 2x;$$

Если $x < 0$, тогда:

$$y = \cos(x — x) = \cos 0 = 1;$$

График функции:

г) $y = \sin\frac{x + 3|x|}{2};$

Если $x \geq 0$, тогда:

$$y = \sin\frac{x + 3x}{2} = \sin 2x;$$

Если $x < 0$, тогда:

$$y = \sin\frac{x — 3x}{2} = \sin(-x) = -\sin x;$$

График функции:

а) $y = \sin(x + |x|)$

1. Рассмотрим случай $x \geq 0$:

Когда $x \geq 0$, то $|x| = x$. Подставим это в выражение функции:

$$y = \sin(x + |x|) = \sin(x + x) = \sin(2x)$$

Таким образом, при $x \geq 0$ функция $y = \sin(x + |x|)$ превращается в $y = \sin(2x)$.

2. Рассмотрим случай $x < 0$:

Когда $x < 0$, то $|x| = -x$. Подставим это в выражение функции:

$$y = \sin(x + |x|) = \sin(x — x) = \sin(0) = 0$$

Таким образом, при $x < 0$ функция $y = \sin(x + |x|)$ всегда равна 0.

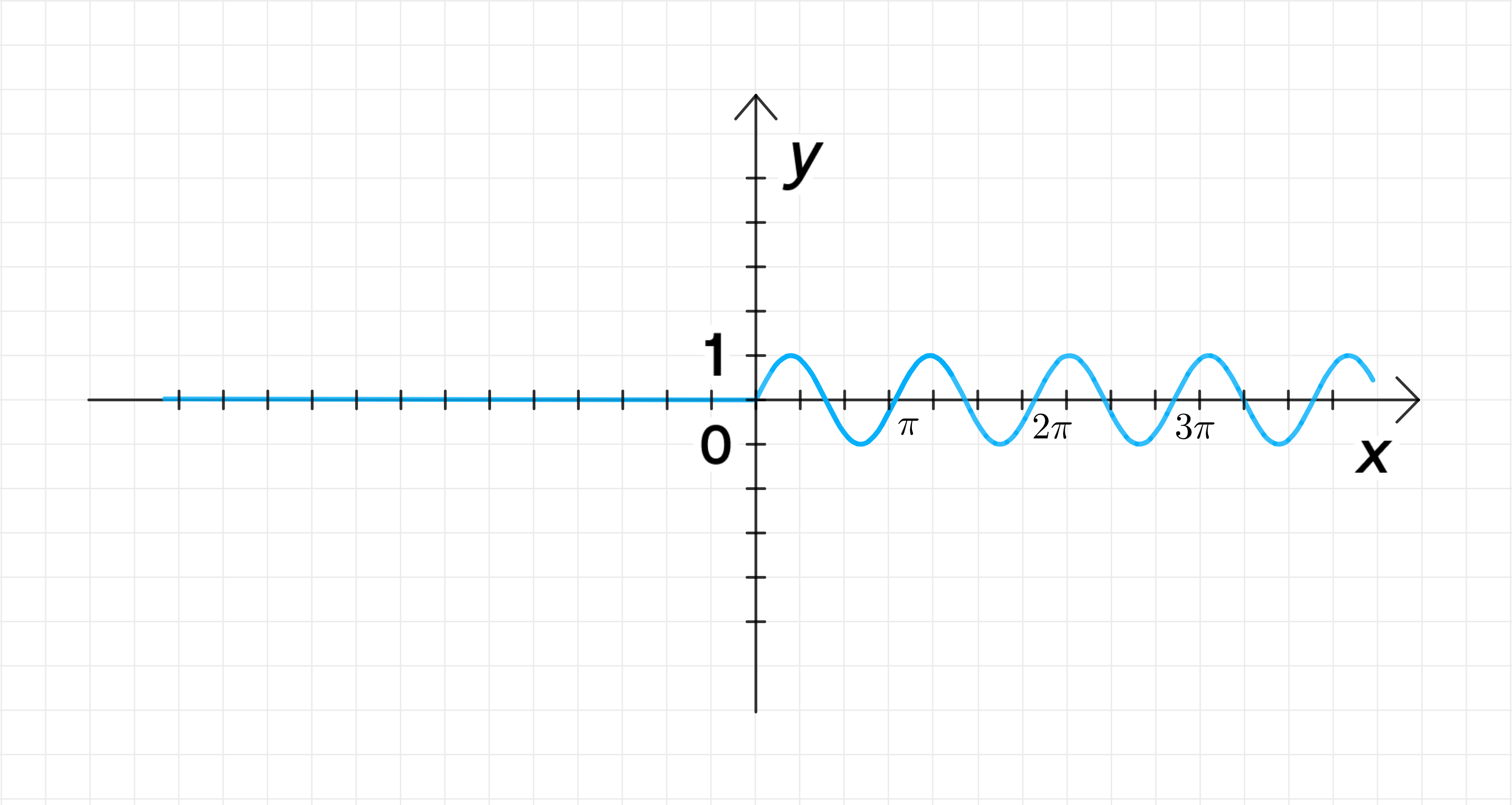
3. Построение графика функции:

График функции состоит из двух частей:

• Для $x \geq 0$ график будет представлять собой синусоиду с аргументом $2x$, то есть амплитуда будет такой же, но период будет в 2 раза меньше, чем у стандартной функции $y = \sin x$.
• Для $x < 0$ график будет горизонтальной линией, равной 0.

График можно представить как синусоиду для $x \geq 0$ и прямую линию $y = 0$ для $x < 0$.

б) $y = \cos\frac{x — 2|x|}{2}$

1. Рассмотрим случай $x \geq 0$:

Когда $x \geq 0$, то $|x| = x$. Подставим это в выражение функции:

$$y = \cos\frac{x — 2|x|}{2} = \cos\frac{x — 2x}{2} = \cos\left(-\frac{x}{2}\right)$$

Из свойств косинуса ($\cos(-\theta) = \cos(\theta)$) получаем:

$$y = \cos\frac{x}{2}$$

Таким образом, при $x \geq 0$ функция превращается в $y = \cos\frac{x}{2}$.

2. Рассмотрим случай $x < 0$:

Когда $x < 0$, то $|x| = -x$. Подставим это в выражение функции:

$$y = \cos\frac{x — 2|x|}{2} = \cos\frac{x + 2x}{2} = \cos\frac{3x}{2}$$

Таким образом, при $x < 0$ функция становится $y = \cos\frac{3x}{2}$.

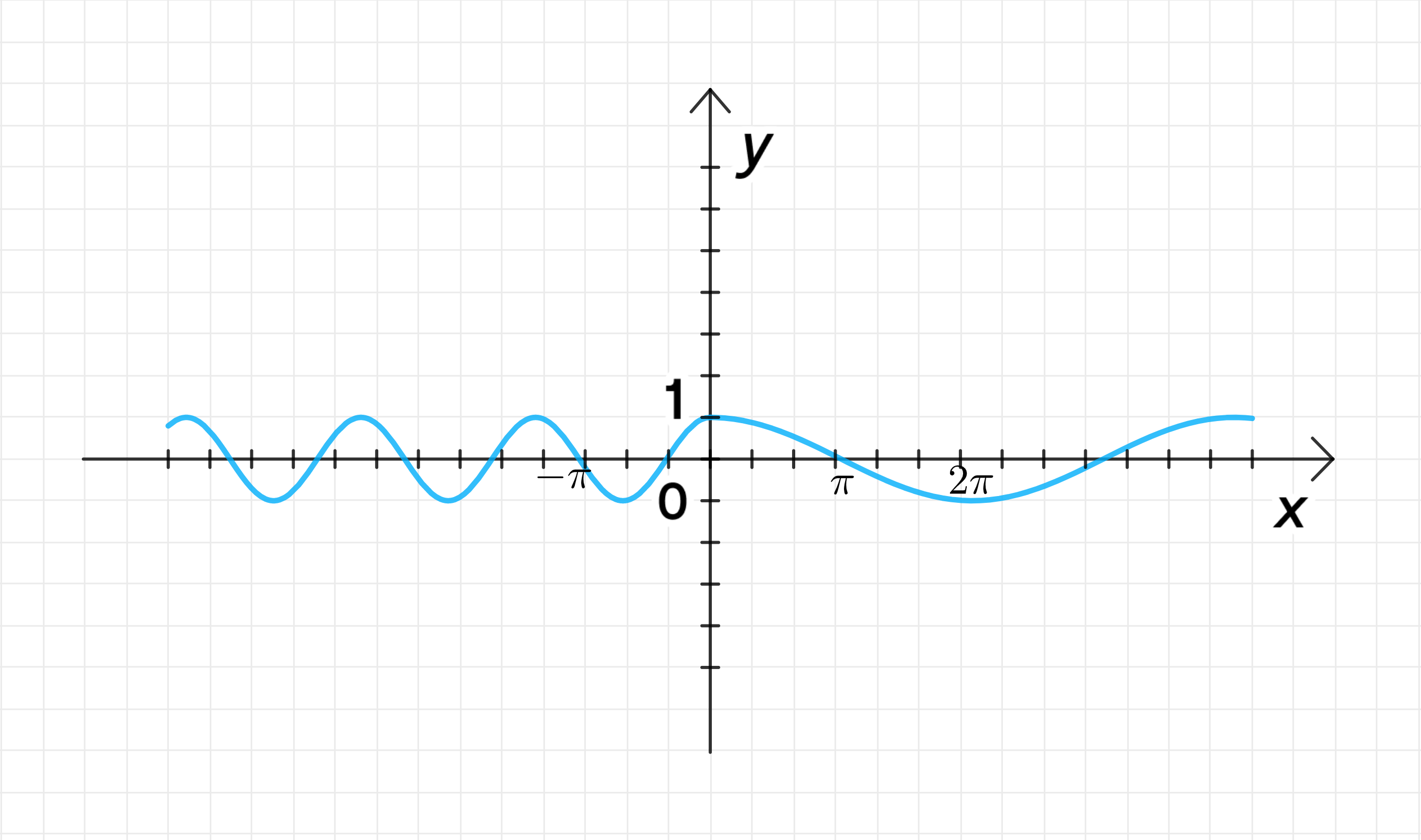
3. Построение графика функции:

• Для $x \geq 0$ график будет представлять собой косинусоиду, где период будет увеличен в 2 раза, то есть $\cos\frac{x}{2}$ имеет больший период, чем стандартная косинусоида.
• Для $x < 0$ график будет представлять собой косинусоиду с периодом, увеличенным в 3 раза (за счет множителя $\frac{3x}{2}$).

График будет состоять из двух частей:

• Для $x \geq 0$ график будет $y = \cos\frac{x}{2}$.
• Для $x < 0$ график будет $y = \cos\frac{3x}{2}$.

в) $y = \cos(x + |x|)$

1. Рассмотрим случай $x \geq 0$:

Когда $x \geq 0$, то $|x| = x$. Подставим это в выражение функции:

$$y = \cos(x + |x|) = \cos(x + x) = \cos(2x)$$

Таким образом, при $x \geq 0$ функция превращается в $y = \cos(2x)$.

2. Рассмотрим случай $x < 0$:

Когда $x < 0$, то $|x| = -x$. Подставим это в выражение функции:

$$y = \cos(x + |x|) = \cos(x — x) = \cos(0) = 1$$

Таким образом, при $x < 0$ функция всегда равна 1.

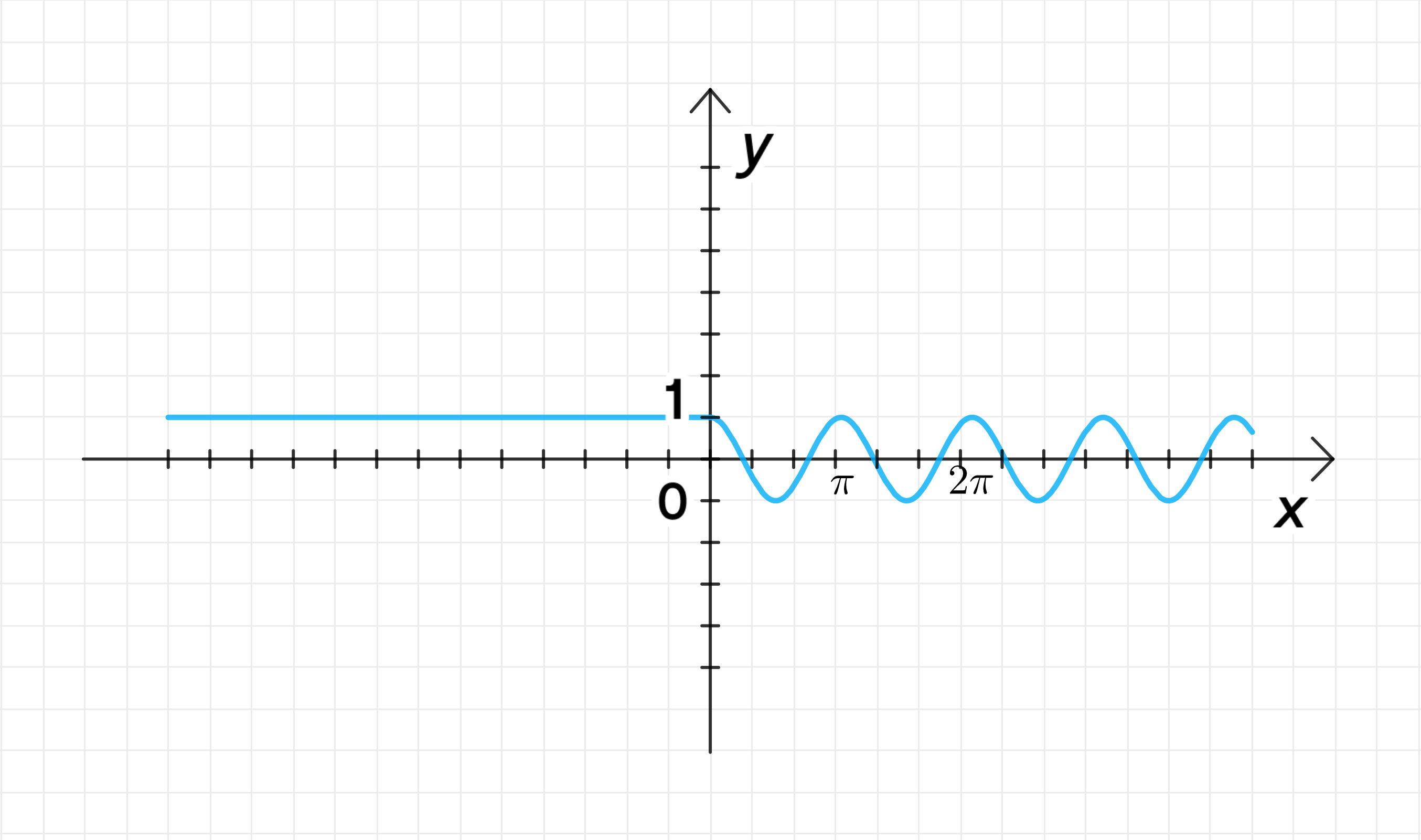
3. Построение графика функции:

• Для $x \geq 0$ график будет представлять собой косинусоиду с аргументом $2x$, что приводит к уменьшению периода косинусоиды в 2 раза.
• Для $x < 0$ график будет горизонтальной линией $y = 1$.

График функции будет выглядеть как косинусоида с увеличенной частотой для $x \geq 0$ и прямую линию $y = 1$ для $x < 0$.

г) $y = \sin\frac{x + 3|x|}{2}$

1. Рассмотрим случай $x \geq 0$:

Когда $x \geq 0$, то $|x| = x$. Подставим это в выражение функции:

$$y = \sin\frac{x + 3|x|}{2} = \sin\frac{x + 3x}{2} = \sin(2x)$$

Таким образом, при $x \geq 0$ функция превращается в $y = \sin(2x)$.

2. Рассмотрим случай $x < 0$:

Когда $x < 0$, то $|x| = -x$. Подставим это в выражение функции:

$$y = \sin\frac{x + 3|x|}{2} = \sin\frac{x — 3x}{2} = \sin\left(-\frac{2x}{2}\right) = -\sin(x)$$

Таким образом, при $x < 0$ функция превращается в $y = -\sin(x)$.

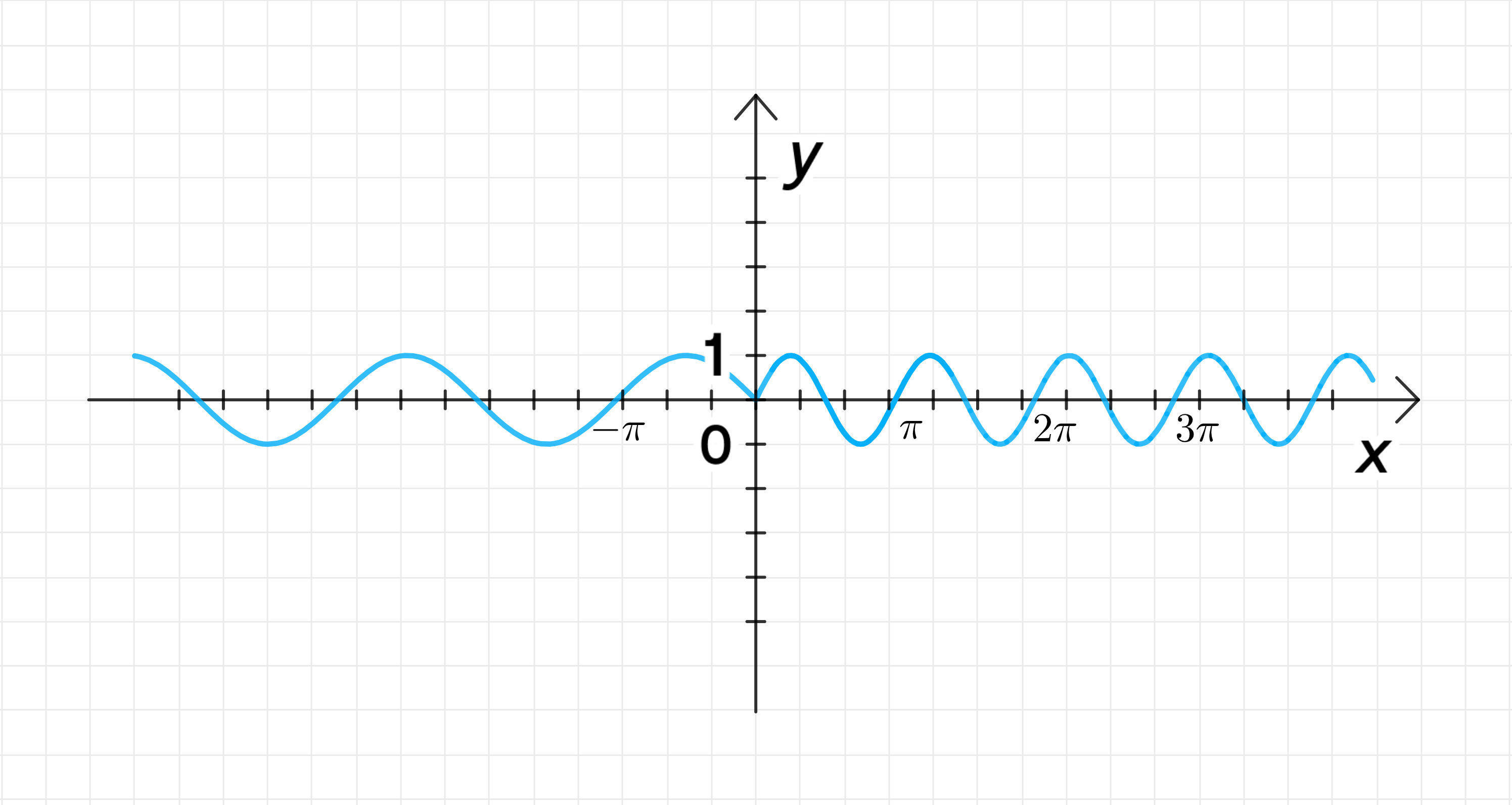
3. Построение графика функции:

• Для $x \geq 0$ график будет представлять собой синусоиду с аргументом $2x$, то есть её период будет в два раза меньше, чем у стандартной синусоиды.
• Для $x < 0$ график будет представлять собой синусоиду с амплитудой, направленной вниз (из-за минусового знака).

График будет выглядеть как синусоида для $x \geq 0$, и зеркальное отражение стандартной синусоиды относительно оси $Ox$ для $x < 0$.