Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 18.2 Профильный Уровень Мордкович — Подробные Ответы
а)
б)
в)
г)
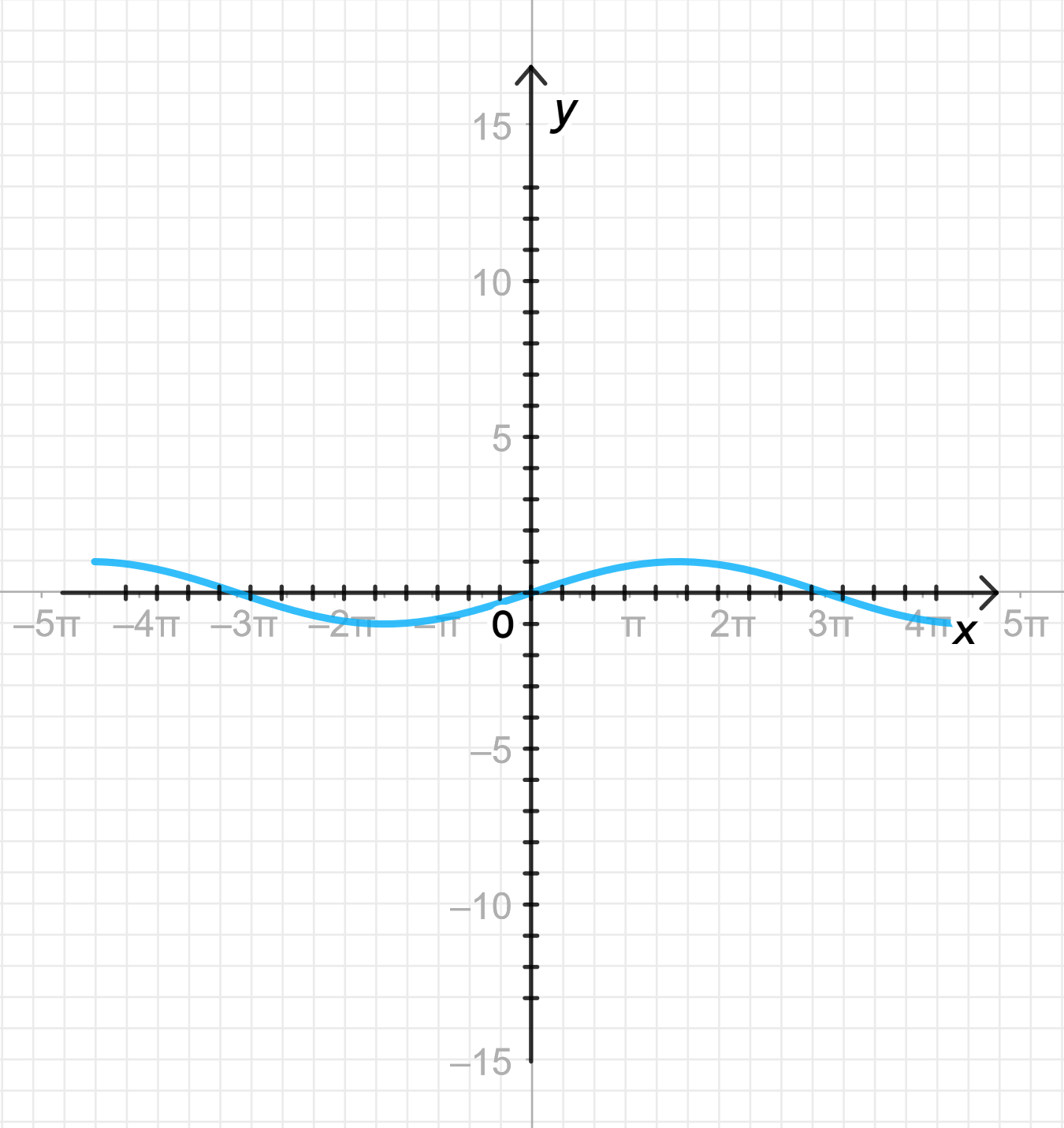
а)
Построим дугу графика ;
Совершим ее растяжение от оси с коэффициентом ;
Достроим график функции:
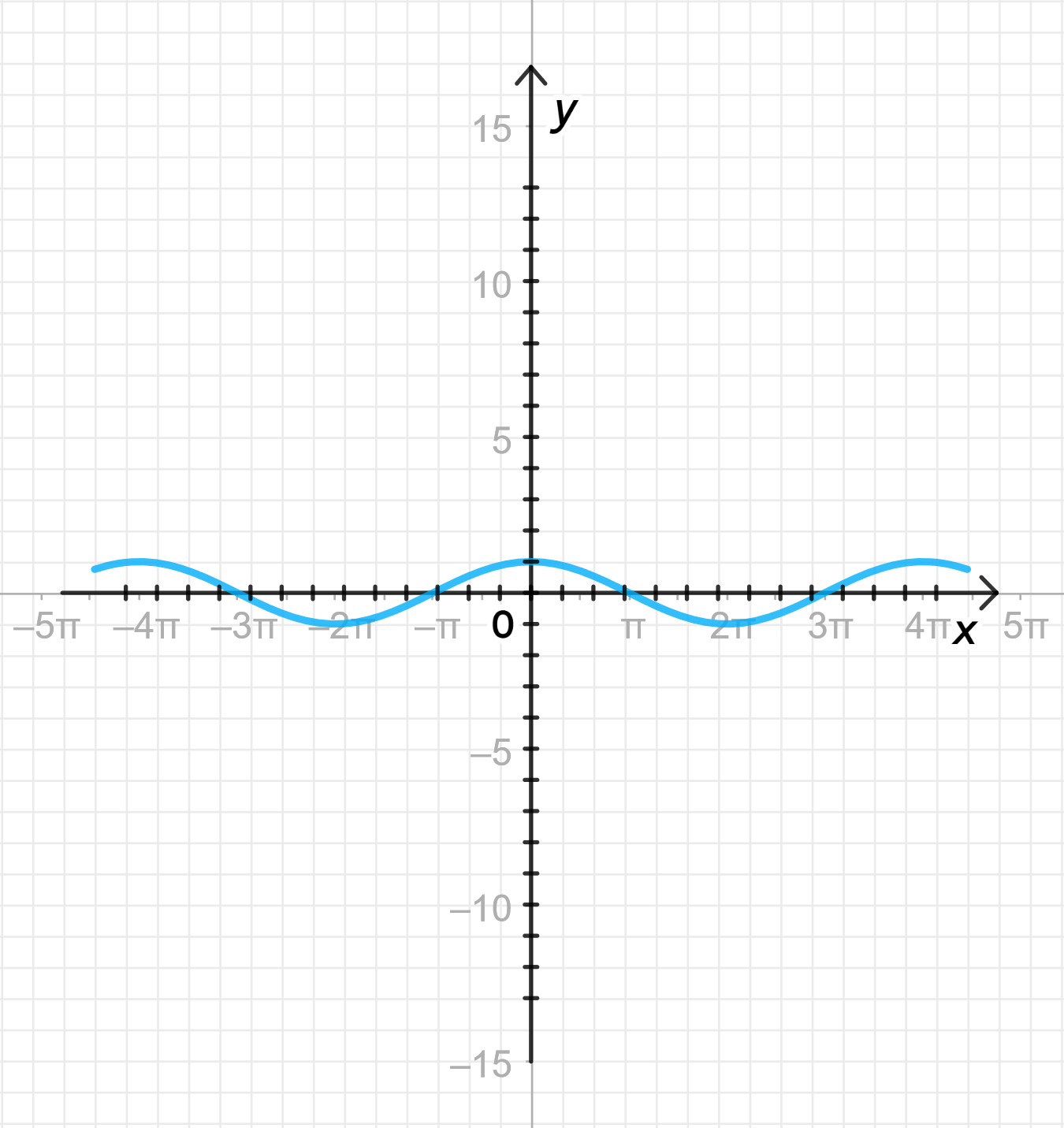
б)
Построим дугу графика ;
Совершим ее сжатие к оси с коэффициентом ;
Достроим график функции:
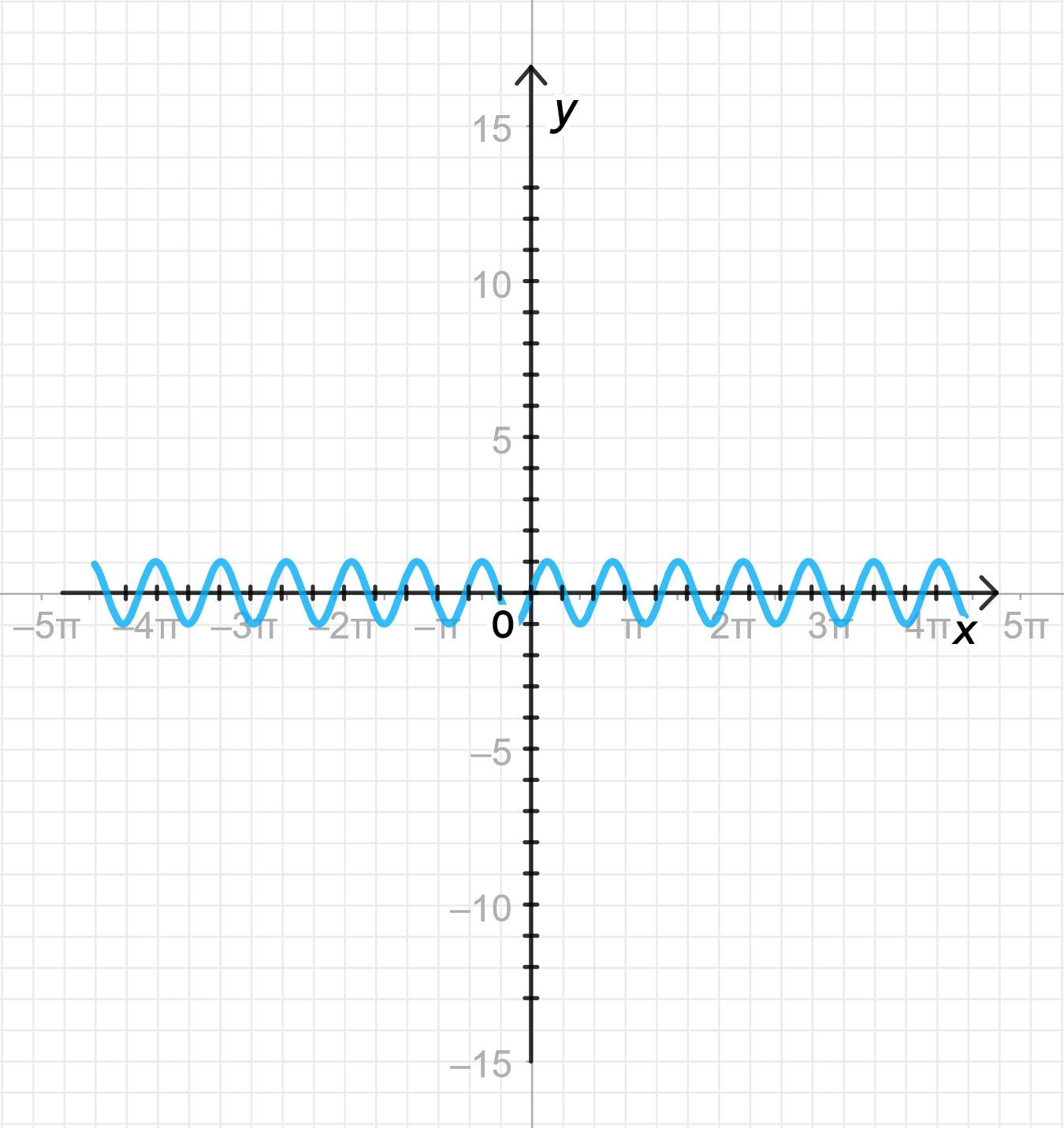
в)
Построим дугу графика ;
Совершим ее растяжение от оси с коэффициентом ;
Достроим график функции:
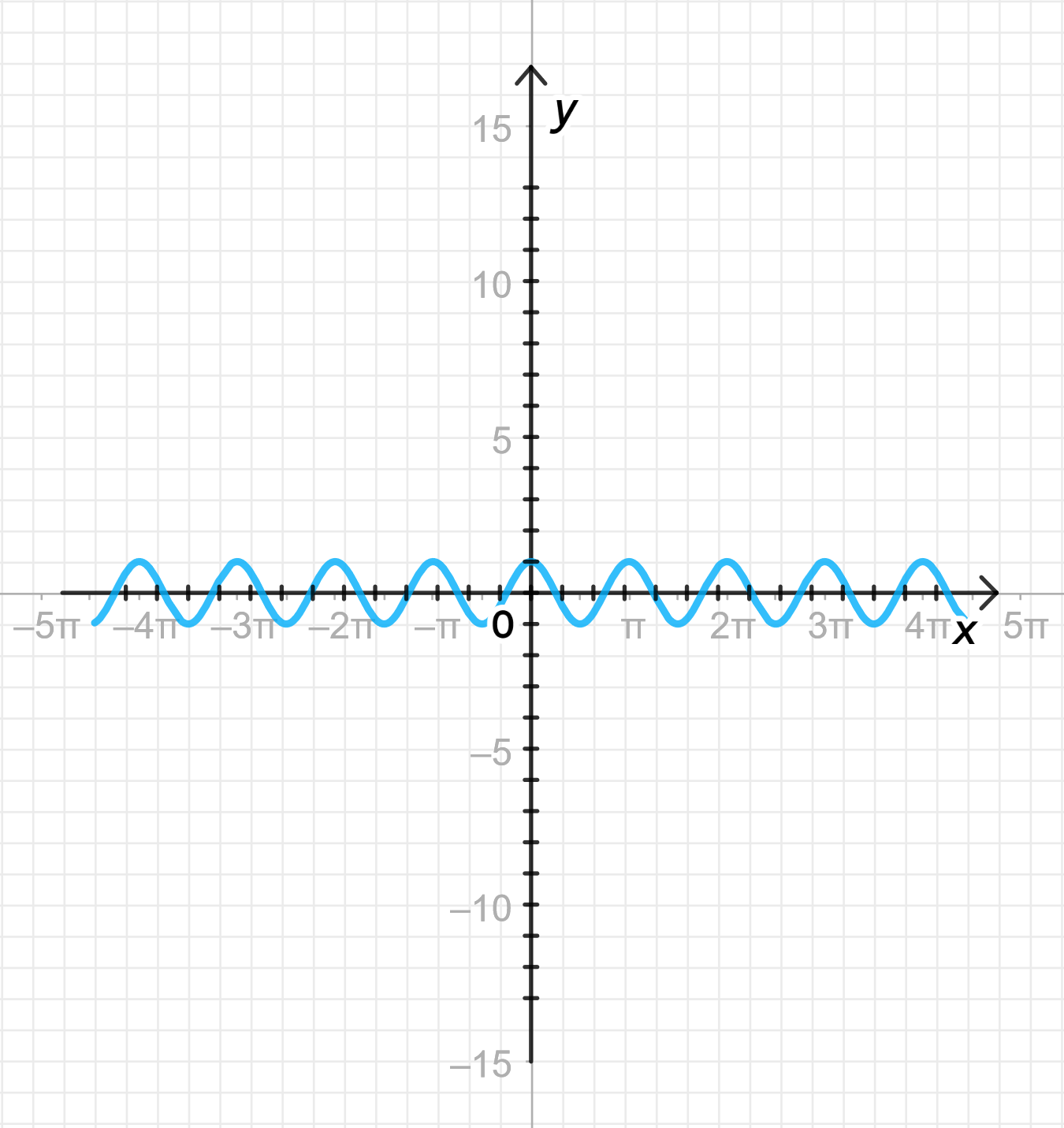
г)
Построим дугу графика ;
Совершим ее сжатие к оси с коэффициентом ;
Достроим график функции:
а)
1) Построение дуги графика
График функции — это стандартная синусоида, которая:
- Имеет период .
- Проходит через начало координат .
- Имеет амплитуду 1, то есть максимальное значение функции , а минимальное — .
- График повторяется с периодичностью .
Для некоторых значений мы можем подсчитать:
- ,
- ,
- ,
- ,
- .
Таблица значений:
| 0 | |||||
|---|---|---|---|---|---|
| 0 | 1 | 0 | -1 | 0 |
График синуса будет начинаться от нуля, подниматься до 1, затем опускаться до -1 и снова возвращаться к нулю через период .
2) Совершим растяжение от оси с коэффициентом
Функция отличается от стандартного графика тем, что аргумент делится на 3. Это приводит к растяжению графика вдоль оси на коэффициент 3.
- Почему растяжение? Функция растягивает график по оси (вдоль горизонтальной оси) на коэффициент 3, что означает, что для каждого значения график функции будет достигать того же значения , но на более широких интервалах по оси .
- Период функции будет равен , так как период синуса определяется как разделённое на множитель, стоящий перед в аргументе.
Таким образом, растяжение графика функции приведёт к увеличению расстояния между пиками и впадинами синусоиды, а сам график станет более «растянутым».
3) Достроим график функции
- Период будет , и график будет повторяться каждый .
- Амплитуда остаётся равной 1, то есть максимальное значение функции , а минимальное — .
- Пик функции теперь будет достигаться не в точках , а в точках .
б)
1) Построение дуги графика
График функции — это стандартная косинусоида, которая:
- Имеет период .
- Проходит через точку .
- Имеет амплитуду 1, то есть максимальное значение функции , а минимальное — .
- График повторяется с периодичностью .
Для некоторых значений :
- ,
- ,
- ,
- ,
- .
Таблица значений:
| 0 | |||||
|---|---|---|---|---|---|
| 1 | 0 | -1 | 0 | 1 |
2) Совершим сжатие к оси с коэффициентом
Функция отличается от стандартной функции тем, что в аргументе стоит множитель 2. Это означает, что график будет сжат по оси .
- Почему сжатие? Если аргумент функции умножен на 2, это уменьшает период функции. Период функции будет равен , то есть график будет повторяться каждый , в два раза быстрее, чем график функции .
- Таким образом, все значения функции будут достигаться в два раза быстрее, и расстояние между пиками и впадинами будет сокращено в два раза.
3) Достроим график функции
- Период функции будет равен .
- Амплитуда остаётся равной 1, то есть максимальное значение функции , а минимальное — .
- Пики и впадины будут располагаться через расстояние .
в)
1) Построение дуги графика
Аналогично предыдущим случаям, начнем с графика функции . Его особенности описаны выше.
2) Совершим растяжение от оси с коэффициентом
Функция отличается от стандартного графика тем, что в её аргументе присутствует множитель , который растягивает график по оси .
- Почему растяжение? Если аргумент функции делится на 2, это увеличивает период функции. Период функции будет равен , то есть график будет повторяться каждый , что в два раза больше периода стандартной косинусоиды .
- Таким образом, график функции будет растянут по оси , и расстояние между пиками и впадинами будет увеличено в два раза.
3) Достроим график функции
- Период функции будет равен .
- Амплитуда остаётся равной 1, то есть максимальное значение функции , а минимальное — .
- Пики и впадины будут располагаться через расстояние .
г)
1) Построение дуги графика
График функции аналогичен тому, который мы построили в пункте а.
2) Совершим сжатие к оси с коэффициентом
Функция отличается от стандартной синусоиды тем, что в её аргументе стоит множитель 3. Это сжимает график функции вдоль оси .
- Почему сжатие? Если аргумент функции умножен на 3, то график будет сжаться вдоль оси , и период функции станет равным .
- Таким образом, график функции будет повторяться быстрее, чем график стандартной синусоиды .
3) Достроим график функции
- Период функции будет равен .
- Амплитуда остаётся равной 1, то есть максимальное значение функции , а минимальное — .
- Пики и впадины будут располагаться через расстояние .