Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 18.3 Профильный Уровень Мордкович — Подробные Ответы
а) ;
б) ;
в) ;
г)
а) ;
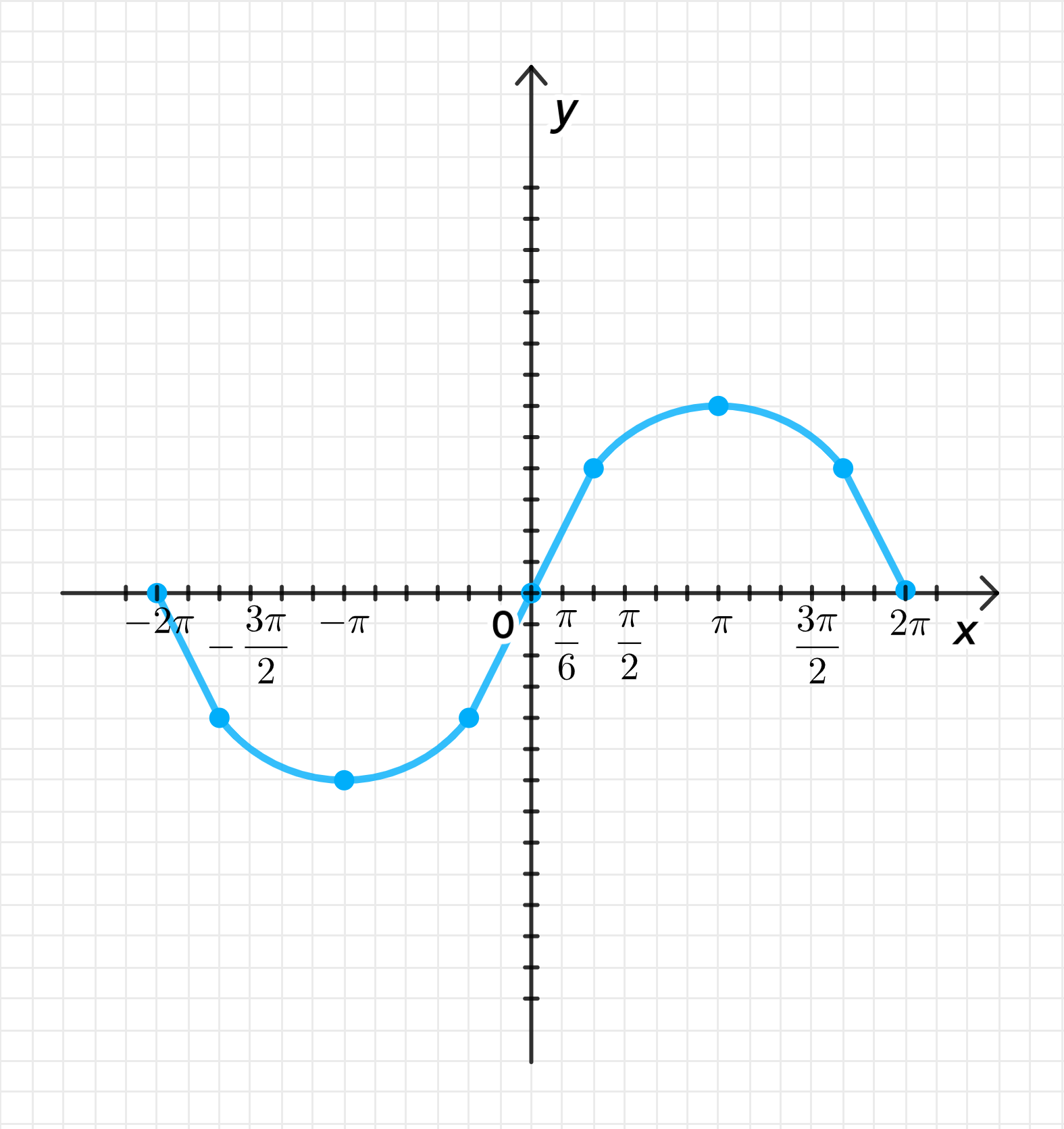
Построим дугу графика , а затем:
- Совершим ее растяжение от оси с коэффициентом ;
- Совершим ее растяжение от оси с коэффициентом ;
Достроим график функции:
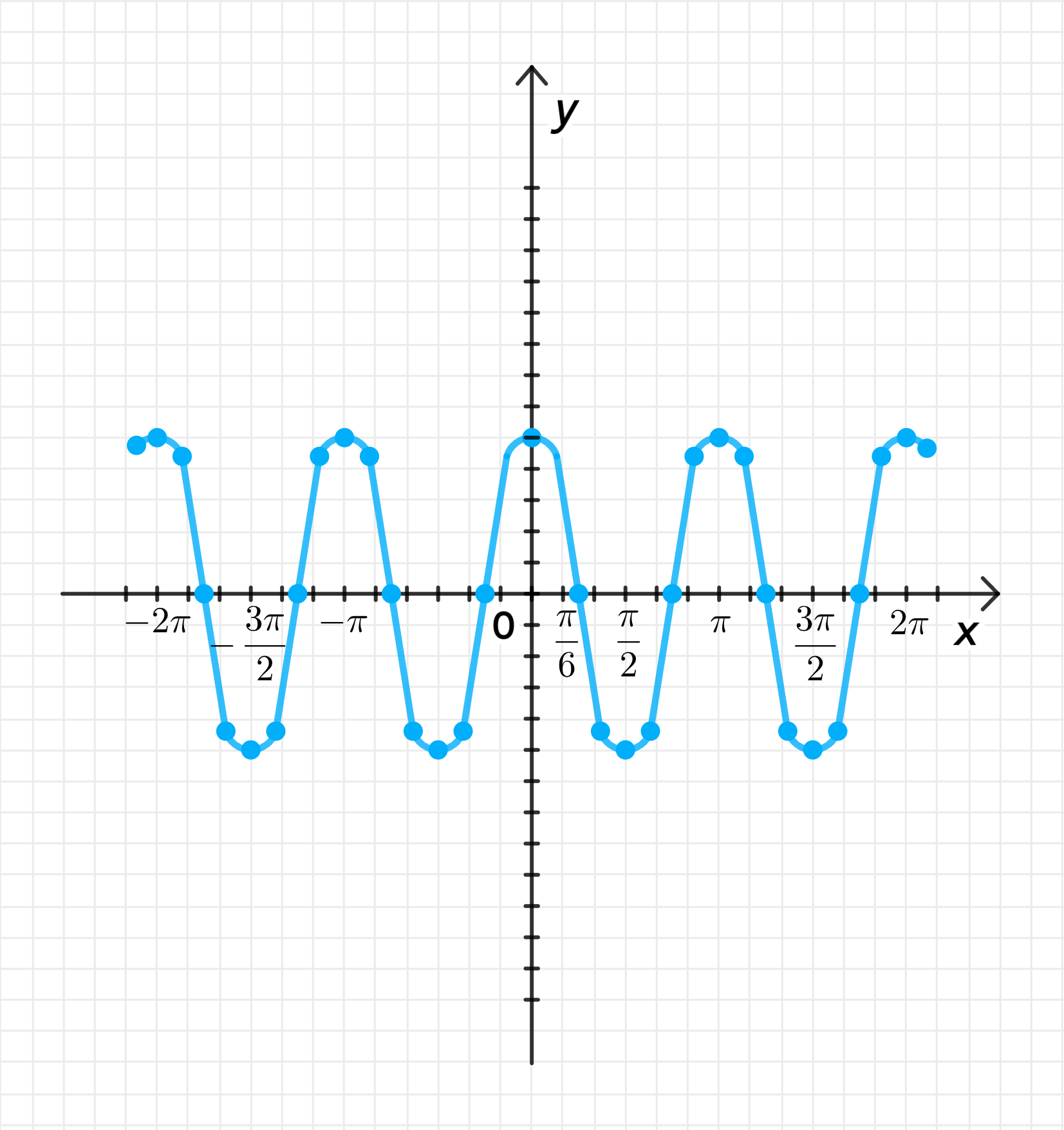
б) ;
Построим дугу графика , а затем:
- Совершим ее сжатие к оси с коэффициентом ;
- Совершим ее растяжение от оси с коэффициентом ;
Достроим график функции:
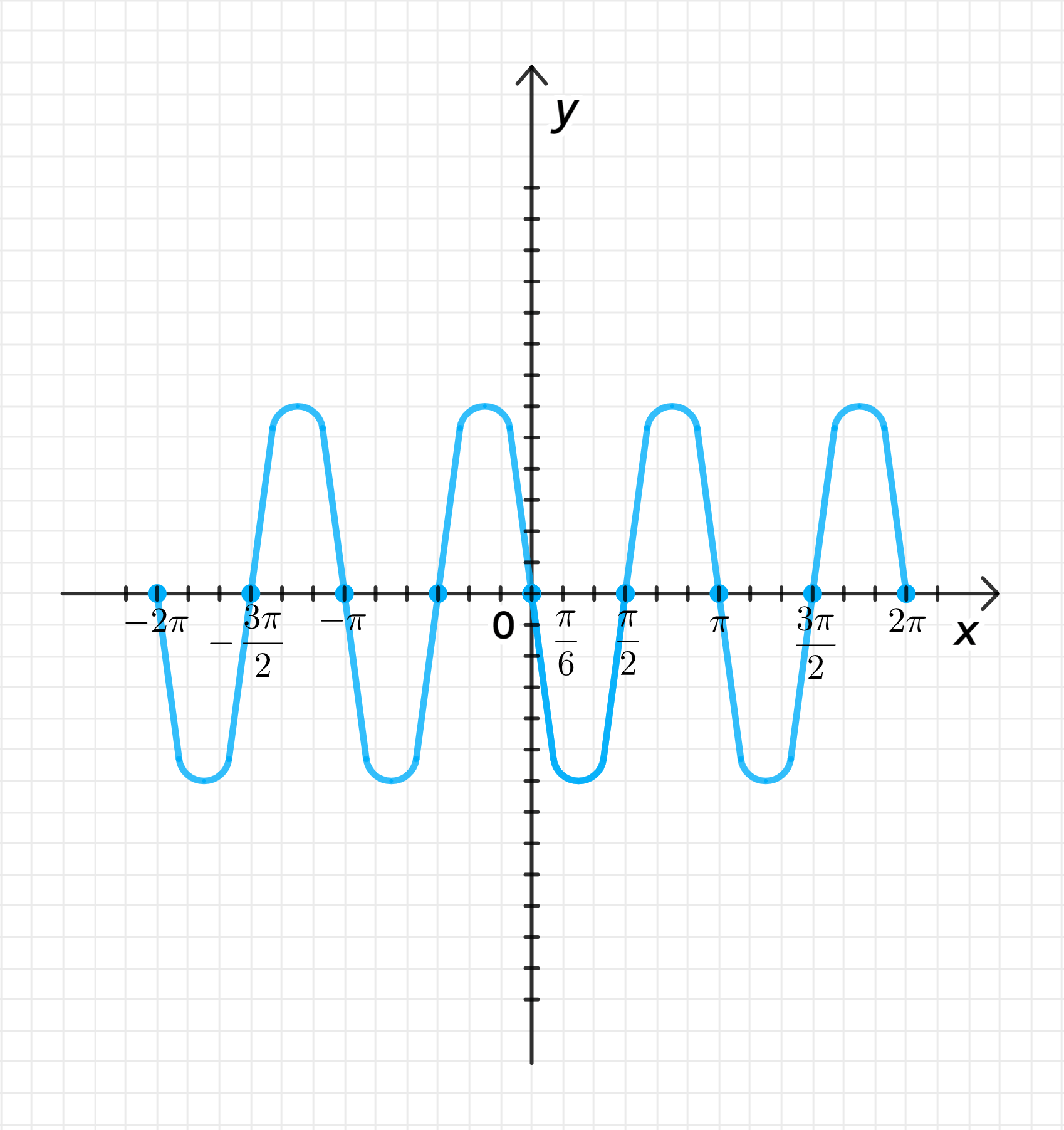
в) ;
Построим дугу графика , а затем:
- Совершим ее сжатие к оси с коэффициентом ;
- Отразим ее относительно оси абсцисс;
- Совершим ее растяжение от оси с коэффициентом ;
Достроим график функции:
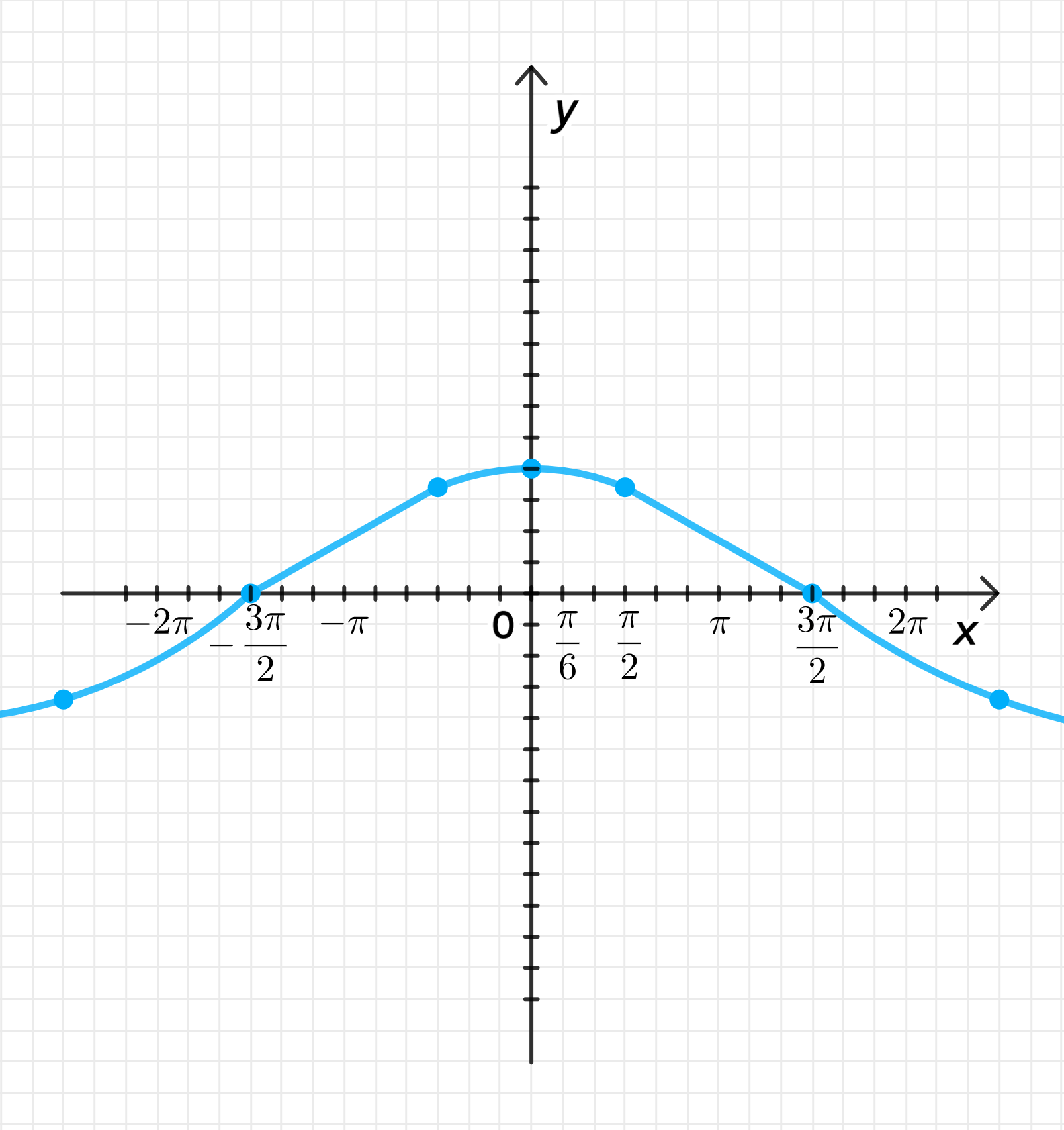
г) ;
Построим дугу графика , а затем:
- Совершим ее растяжение от оси с коэффициентом ;
- Совершим ее растяжение от оси с коэффициентом ;
Достроим график функции:
а)
1) Построение дуги графика
График функции представляет собой стандартную синусоиду с амплитудой 1 и периодом . Стандартные характеристики:
- Период .
- Амплитуда = 1.
- Функция проходит через , достигает максимума , минимума , и снова возвращается к нулю в точке .
Таблица значений для :
| 0 | |||||
|---|---|---|---|---|---|
| 0 | 1 | 0 | -1 | 0 |
График будет выглядеть как плавная волна, начинающаяся от нуля, достигающая пика в , затем опускающаяся до минимума в и возвращающаяся к нулю.
2) Совершим растяжение от оси с коэффициентом
Когда в функции аргумент умножается или делится на какое-то число, это влияет на горизонтальное растяжение или сжатие графика. В данном случае у нас , где в аргументе функции присутствует множитель .
Это приводит к увеличению периода синусоиды в два раза. Чтобы понять это, вспомним, что период функции равен , и если аргумент синуса становится , то период увеличивается до .
Таким образом, график растягивается вдоль оси , и вся волна будет повторяться не через , а через .
3) Совершим растяжение от оси с коэффициентом
Теперь, что касается вертикального растяжения: функция имеет коэффициент перед синусом. Это означает, что все значения функции будут умножаться на 3.
- Амплитуда функции становится .
- Максимальное значение будет равно 3, минимальное значение будет равно -3, и график будет колебаться между этими значениями.
Растяжение вдоль оси в 3 раза делает график более высокими пиками и глубокими впадинами.
4) Достроим график функции
- Период графика функции будет .
- Амплитуда будет 3.
- Функция будет начинаться от , достигать , опускаться до и возвращаться к .
График будет иметь растянутую по горизонтали форму и увеличенные пики и впадины.
б)
1) Построение дуги графика
График функции является стандартной косинусоидой с амплитудой 1 и периодом . Он будет выглядеть следующим образом:
- Период .
- Амплитуда = 1.
- График начинается с точки , опускается до , возвращается к нулю в , и снова достигает максимума в .
Таблица значений для :
| 0 | |||||
|---|---|---|---|---|---|
| 1 | 0 | -1 | 0 | 1 |
2) Совершим сжатие к оси с коэффициентом
В функции присутствует множитель 2 в аргументе косинуса. Это уменьшает период функции, сжимая график по оси .
- Период функции будет , то есть график будет повторяться в два раза быстрее.
- Каждые будет проходить полный цикл: от максимума до минимума и обратно.
3) Совершим растяжение от оси с коэффициентом
Множитель 2,5 перед косинусом означает, что амплитуда функции увеличится в 2,5 раза. То есть:
- Амплитуда графика станет 2,5.
- График функции будет колебаться между значениями и .
4) Достроим график функции
- Период будет равен .
- Амплитуда будет 2,5.
- График будет колебаться между значениями и .
в)
1) Построение дуги графика
График функции аналогичен тому, который мы построили в пункте а.
2) Совершим сжатие к оси с коэффициентом
Функция включает множитель 2 в аргументе синуса, что сжимает график по оси и делает период функции равным .
3) Отражаем график относительно оси абсцисс
Множитель перед синусом означает, что весь график будет отражен относительно оси . Функция будет колебаться между значениями и , но при этом график будет инвертирован по вертикали, то есть пики и впадины поменяются местами.
4) Совершим растяжение от оси с коэффициентом
Растяжение по оси с коэффициентом 3 означает, что амплитуда будет равна 3.
5) Достроим график функции
- Период функции будет равен .
- Амплитуда будет 3.
- График будет колебаться между и , но будет инвертирован по вертикали.
г)
1) Построение дуги графика
График функции также строится как стандартная косинусоида, как в предыдущих примерах.
2) Совершим растяжение от оси с коэффициентом
В функции , множитель перед косинусом означает, что амплитуда будет равна 2. Таким образом, график будет колебаться между и .
3) Совершим растяжение от оси с коэффициентом
Деление аргумента на 3 растягивает график по оси . Период функции будет , так как новый период функции будет равен , что в 3 раза больше стандартного периода .
4) Достроим график функции
- Период будет .
- Амплитуда будет 2.
- График будет колебаться между значениями и и повторяться через .