ГДЗ по Алгебре 10 Класс Номер 18.4 Профильный Уровень Мордкович — Подробные Ответы

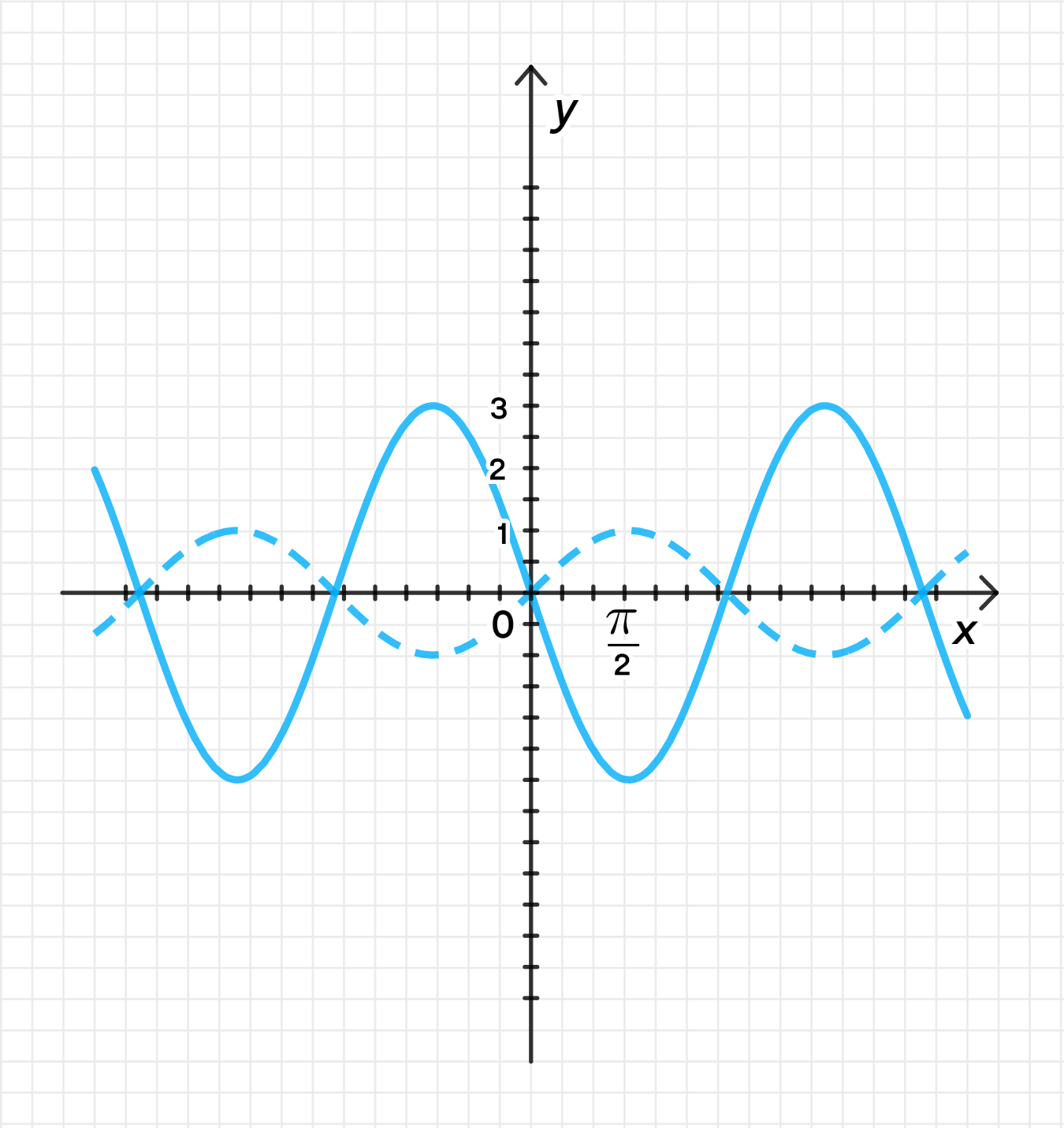
а) у = 3sin(-x);

б) у = -2cos(-3x);

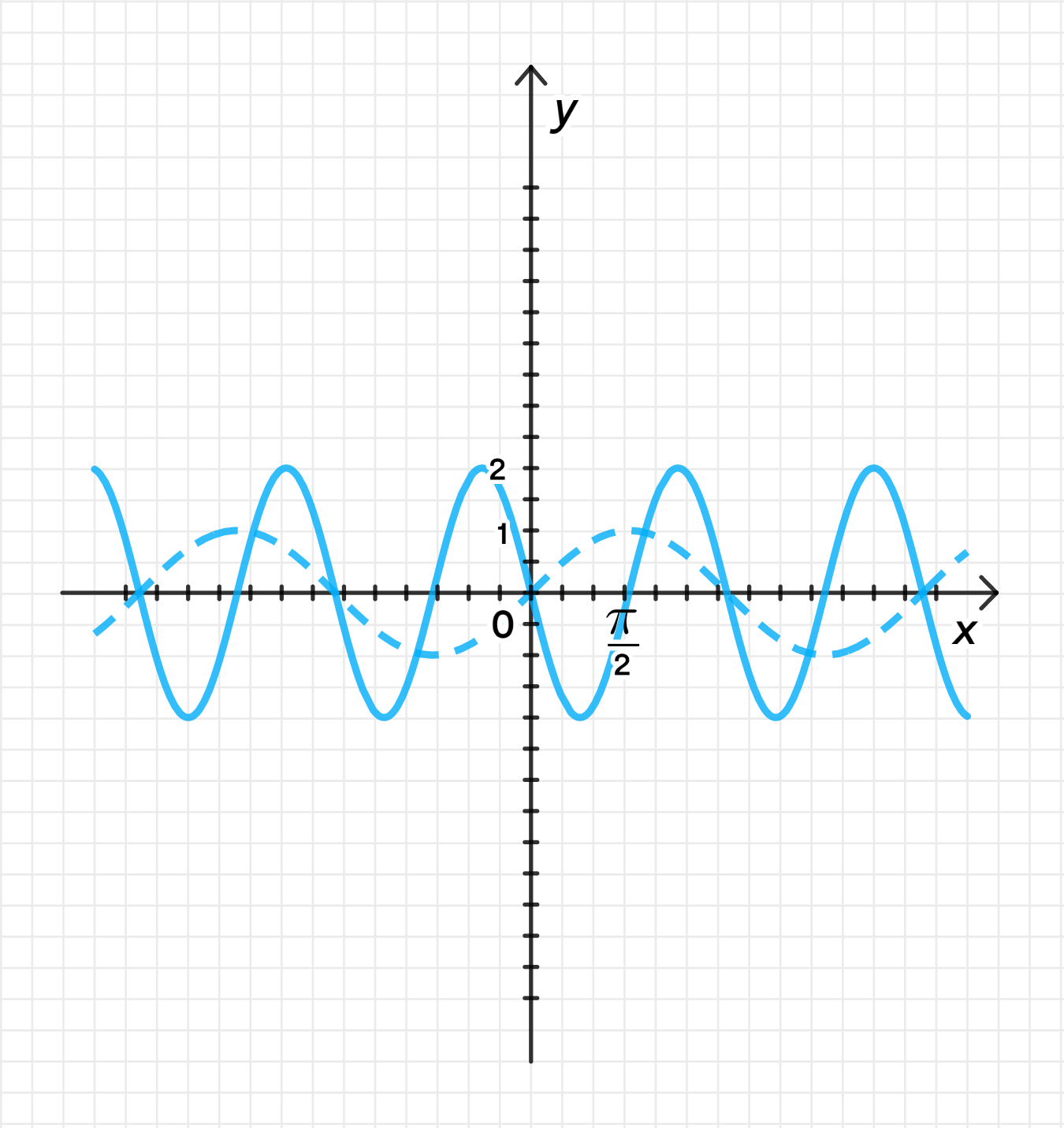
в) у = 2sin(-2x);

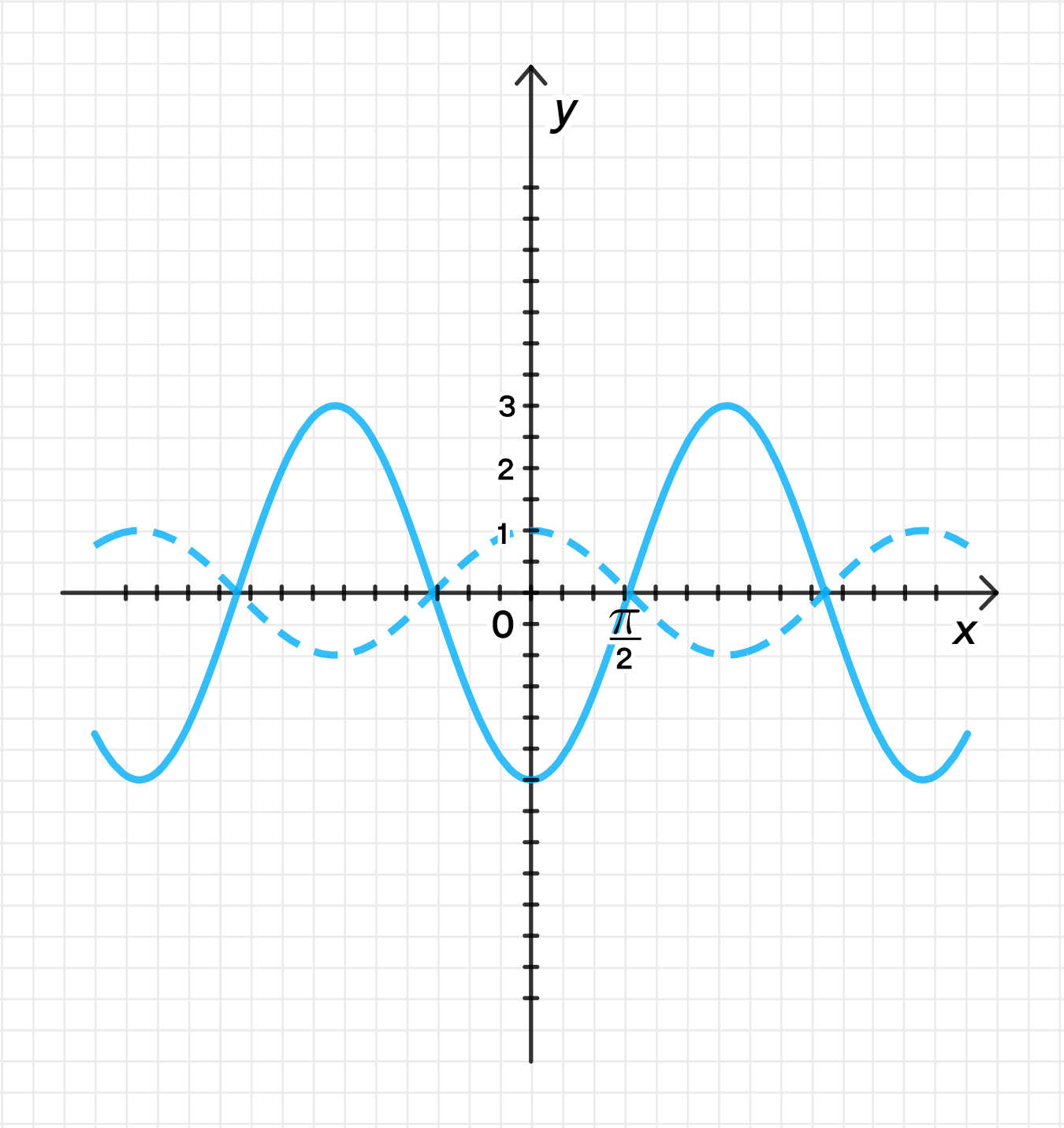
г) у = -3cos(-x).

а) $y=3\sin (-x)=-3\sin x$;

Построим дугу графика $y=\sin x$, а затем:

• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k=3$;

Достроим график функции:

б) $y=-2\cos (-3x)=-2\cos 3x$;

Построим дугу графика $y=\cos x$, а затем:

• Совершим ее сжатие к оси $Oy$ с коэффициентом $k=3$;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k=2$;

Достроим график функции:

в) $y=2\sin (-2x)=-2\sin 2x$;

Построим дугу графика $y=\sin x$, а затем:

• Совершим ее сжатие к оси $Oy$ с коэффициентом $k=2$;
• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k=2$;

Достроим график функции:

г) $y=-3\cos (-x)=-3\cos x$;

Построим дугу графика $y=\cos x$, а затем:

• Отразим ее относительно оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k=3$;

Достроим график функции:

а) $y=3\sin (-x)=-3\sin x$

1) Построение дуги графика $y=\sin x$

График функции $y=\sin x$ — это стандартная синусоида, которая:

• Имеет период $2\pi$.
• Проходит через начало координат $(0,0)$.
• Имеет амплитуду 1, то есть максимальное значение $y=1$, а минимальное — $y=-1$.
• График повторяется с периодичностью $2\pi$, создавая плавную волну.

Некоторые значения функции:

• $\sin 0=0$,
• $\sin \left(\frac{\pi }{2}\right)=1$,
• $\sin (\pi )=0$,
• $\sin \left(\frac{3\pi }{2}\right)=-1$,
• $\sin (2\pi )=0$.

Таблица значений:

2) Отражение относительно оси абсцисс

Для функции $y=3\sin (-x)=-3\sin x$ у нас есть два преобразования. Первое из них — это отражение относительно оси абсцисс.

• Сначала, если бы у нас была функция $y=\sin (-x)$, то график просто перевернулся бы относительно оси $y$. Однако, так как синус — это четная функция, то $\sin (-x)=\sin (x)$. Но в данном случае у нас стоит минус перед синусом, что отражает весь график относительно оси $x$, то есть все значения $y$ поменяют знак.
• Получаем график функции $y=-\sin x$, который просто зеркально отображает график $y=\sin x$ относительно оси $x$.

3) Растяжение по оси $Oy$ с коэффициентом $k=3$

Следующий шаг — растяжение графика по вертикали (по оси $y$) с коэффициентом 3.

• Умножение на 3 приводит к тому, что амплитуда синусоиды увеличивается в 3 раза. Максимальное значение функции теперь будет равно 3, а минимальное — -3.
• График будет колебаться между значениями $y=3$ и $y=-3$, но форма синусоиды сохранится.

4) Достроим график функции

• Период функции не изменяется, он остается равным $2\pi$, так как в аргументе синуса нет множителя, изменяющего период.
• Амплитуда графика становится 3, то есть максимальное значение $y=3$, а минимальное $y=-3$.
• График будет симметричен относительно оси $x$, поскольку функция четная, но значения будут более растянутыми по вертикали.

б) $y=-2\cos (-3x)=-2\cos 3x$

1) Построение дуги графика $y=\cos x$

График функции $y=\cos x$ представляет собой стандартную косинусоиду с:

• Периодом $2\pi$.
• Амплитудой 1.
• Начинается с точки $(0,1)$, падает до минимума в $\pi$, и снова возвращается к 1 в точке $2\pi$.

Таблица значений:

2) Сжатие к оси $Oy$ с коэффициентом $k=3$

Функция $y=\cos 3x$ отличается от $y=\cos x$ тем, что аргумент $x$ умножен на 3. Это изменяет период графика.

• Период функции $y=\cos 3x$ будет равен $\frac{2\pi }{3}$, то есть функция будет повторяться в 3 раза быстрее.
• Сжатие по оси $x$ происходит за счет множителя 3 перед $x$, и график будет «сжаться» по горизонтали.

3) Отражение относительно оси абсцисс

Множитель $-2$ перед косинусом отражает график относительно оси $x$. То есть все значения функции $y$ меняют знак, и график инвертируется по вертикали.

• Если раньше функция $y=\cos 3x$ колебалась между $y=1$ и $y=-1$, то теперь она будет колебаться между $y=-2$ и $y=2$, так как амплитуда увеличивается в два раза.

4) Растяжение от оси $Ox$ с коэффициентом $k=2$

Амплитуда функции $y=-2\cos 3x$ увеличена в 2 раза. Это растягивает график вдоль оси $y$.

• Растяжение амплитуды приводит к тому, что значения функции будут колебаться между $y=2$ и $y=-2$.

5) Достроим график функции

• Период будет $\frac{2\pi }{3}$.
• Амплитуда будет 2.
• График будет отражен относительно оси $x$, с периодом $\frac{2\pi }{3}$ и амплитудой 2.

в) $y=2\sin (-2x)=-2\sin 2x$

1) Построение дуги графика $y=\sin x$

График функции $y=\sin x$ аналогичен тому, который мы рассмотрели в пункте а.

2) Сжатие к оси $Oy$ с коэффициентом $k=2$

Функция $y=\sin 2x$ включает множитель 2 в аргументе синуса, что уменьшает период графика. Период функции:

• Период функции $y=\sin 2x$ будет $\frac{2\pi }{2}=\pi$.
• Сжатие графика происходит вдоль оси $x$, и расстояние между пиками и впадинами уменьшается.

3) Отражение относительно оси абсцисс

Множитель $-2$ перед синусом отражает график относительно оси $x$. Это инвертирует все значения функции по вертикали.

• Таким образом, амплитуда остаётся 2, но все пики и впадины меняются местами.

4) Растяжение от оси $Ox$ с коэффициентом $k=2$

После отражения, растяжение графика по оси $y$ на коэффициент 2 увеличивает амплитуду. Теперь значения функции будут колебаться между $y=2$ и $y=-2$.

5) Достроим график функции

• Период будет равен $\pi$.
• Амплитуда будет 2.
• График будет колебаться между значениями $y=2$ и $y=-2$, инвертированный по вертикали.

г) $y=-3\cos (-x)=-3\cos x$

1) Построение дуги графика $y=\cos x$

Как уже упоминалось, график функции $y=\cos x$ является стандартной косинусоидой.

2) Отражение относительно оси абсцисс

Множитель $-3$ перед косинусом приводит к отражению графика относительно оси $x$, а также изменяет амплитуду.

• График будет инвертирован по вертикали, и значения функции будут колебаться между $y=3$ и $y=-3$, так как амплитуда функции стала 3.

3) Растяжение от оси $Ox$ с коэффициентом $k=3$

Амплитуда функции $y=-3\cos x$ теперь равна 3, то есть значения функции будут колебаться между $y=3$ и $y=-3$, но форма графика будет инвертирована.

4) Достроим график функции

• Период функции $y=\cos x$ остаётся равным $2\pi$.
• Амплитуда будет 3.
• График будет инвертирован относительно оси $x$, и значения будут колебаться между $y=3$ и $y=-3$.