ГДЗ по Алгебре 10 Класс Номер 18.7 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \sin 2x — 1$;

б) $y = \cos \frac{x}{2} + 1$;

в) $y = \cos 2x + 3$;

г) $y=\sin \frac{x}{3}-2$

а) $y = \sin 2x — 1$;

Построим дугу графика $y = \sin x$, а затем:

• Совершим ее сжатие к оси $Oy$ с коэффициентом $k = 2$;
• Переместим ее на 1 единицу вниз вдоль оси ординат;

Достроим график функции:

б) $y = \cos \frac{x}{2} + 1$;

Построим дугу графика $y = \cos x$, а затем:

• Совершим ее растяжение от оси $Oy$ с коэффициентом $k = 2$;
• Переместим ее на 1 единицу вверх вдоль оси ординат;

Достроим график функции:

в) $y = \cos 2x + 3$;

Построим дугу графика $y = \cos x$, а затем:

• Совершим ее сжатие к оси $Oy$ с коэффициентом $k = 2$;
• Переместим ее на 3 единицы вверх вдоль оси ординат;

Достроим график функции:

г) $y = \sin \frac{x}{3} — 2$;

Построим дугу графика $y = \sin x$, а затем:

• Совершим ее растяжение от оси $Oy$ с коэффициентом $k = 3$;
• Переместим ее на 2 единицы вниз вдоль оси ординат;

Достроим график функции:

а) $y = \sin 2x — 1$

1) Построение графика функции $y = \sin x$

Стандартный график функции $y = \sin x$ — это синусоида с:

• Периодом $T = 2\pi$,
• Амплитудой 1,
• График проходит через начало координат $(0, 0)$,
• Максимальное значение функции $y = 1$ и минимальное $y = -1$,
• График повторяется через $2\pi$.

Таблица значений для функции $y = \sin x$:

График выглядит как плавная волна, начинающаяся с нуля, достигающая максимума в $\frac{\pi}{2}$, минимума в $\frac{3\pi}{2}$ и возвращается к нулю в точке $2\pi$.

2) Сжатие графика к оси $Oy$ с коэффициентом $k = 2$

Когда перед аргументом функции появляется множитель 2, то период функции изменяется. Период синусоиды $y = \sin 2x$ будет уменьшен в два раза, так как:

$$T = \frac{2\pi}{2} = \pi.$$

Это означает, что график функции теперь будет повторяться каждые $\pi$ единиц по оси $x$. График станет более «сжатым» по горизонтали, так как каждый цикл будет занимать в два раза меньше пространства.

3) Перемещение на 1 единицу вниз вдоль оси ординат

Добавление $-1$ к функции $y = \sin 2x$ означает, что весь график будет сдвинут на 1 единицу вниз. То есть все значения функции теперь будут на 1 меньше, чем в случае с функцией $y = \sin 2x$.

• Максимальное значение функции теперь будет равно $0$ (раньше было $1$),
• Минимальное значение функции теперь будет равно $-2$ (раньше было $-1$).

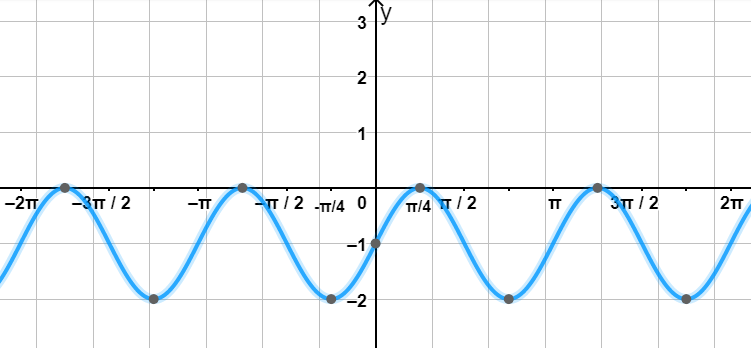
4) Достроим график функции

Теперь мы можем построить полный график функции $y = \sin 2x — 1$:

• Период функции $T = \pi$,
• Амплитуда $1$,
• График колеблется между $-2$ и $0$, сдвинут вниз на 1 единицу.

б) $y = \cos \frac{x}{2} + 1$

1) Построение графика функции $y = \cos x$

График функции $y = \cos x$ также является стандартной косинусоидой с:

• Периодом $T = 2\pi$,
• Амплитудой 1,
• График начинается с точки $(0, 1)$,
• Максимальное значение $y = 1$ и минимальное $y = -1$,
• График повторяется через $2\pi$.

Таблица значений для функции $y = \cos x$:

График функции начинается с максимума в точке $x = 0$, затем идет вниз до минимума в $x = \pi$, и снова возвращается к максимальному значению в точке $x = 2\pi$.

2) Растяжение графика от оси $Oy$ с коэффициентом $k = 2$

Перед функцией стоит коэффициент $\frac{1}{2}$, который изменяет период. Для функции $y = \cos \frac{x}{2}$, новый период будет:

$$T = 2\pi \times 2 = 4\pi.$$

Это растягивает график вдоль оси $x$, и теперь он будет повторяться каждые $4\pi$.

3) Перемещение на 1 единицу вверх вдоль оси ординат

Теперь добавляется $+1$, что сдвигает график вверх на 1 единицу. То есть все значения функции будут увеличены на 1.

• Максимальное значение теперь будет равно $2$ (раньше было $1$),
• Минимальное значение теперь будет равно $0$ (раньше было $-1$).

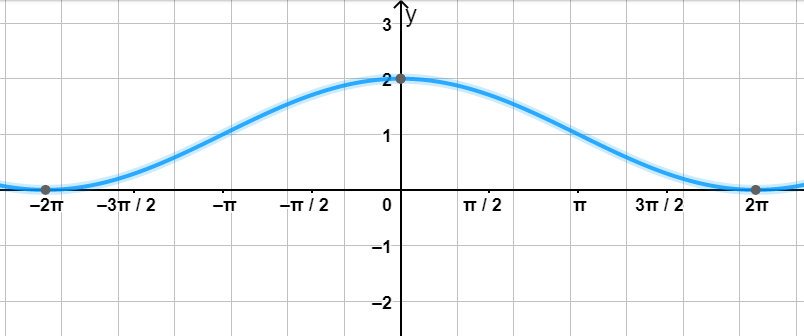
4) Достроим график функции

Теперь мы можем построить график функции $y = \cos \frac{x}{2} + 1$:

• Период функции $T = 4\pi$,
• Амплитуда $1$,
• График будет колебаться между $0$ и $2$, сдвинут вверх на 1 единицу.

в) $y = \cos 2x + 3$

1) Построение графика функции $y = \cos x$

График функции $y = \cos x$ является стандартной косинусоидой, как в предыдущем примере, с:

• Периодом $T = 2\pi$,
• Амплитудой 1,
• График проходит через точку $(0, 1)$,
• Максимальное значение $y = 1$ и минимальное $y = -1$.

2) Сжатие графика к оси $Oy$ с коэффициентом $k = 2$

Функция $y = \cos 2x$ имеет множитель 2 в аргументе, который сжимает график по оси $x$. Период функции:

$$T = \frac{2\pi}{2} = \pi.$$

Это означает, что график будет повторяться через $\pi$, и мы получим более сжатую косинусоиду, чем обычная $y = \cos x$.

3) Перемещение на 3 единицы вверх вдоль оси ординат

Добавление $+3$ сдвигает весь график вверх на 3 единицы. Все значения функции будут увеличены на 3.

• Максимальное значение теперь будет равно $4$ (раньше было $1$),
• Минимальное значение теперь будет равно $2$ (раньше было $-1$).

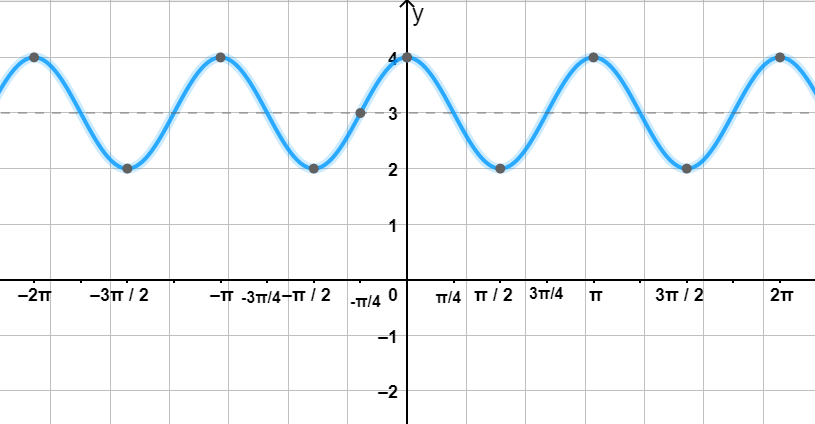
4) Достроим график функции

Теперь мы можем построить график функции $y = \cos 2x + 3$:

• Период функции $T = \pi$,
• Амплитуда $1$,
• График будет колебаться между $2$ и $4$, сдвинут вверх на 3 единицы.

г) $y = \sin \frac{x}{3} — 2$

1) Построение графика функции $y = \sin x$

График функции $y = \sin x$ как обычно имеет:

• Период $T = 2\pi$,
• Амплитуду 1,
• График начинается с точки $(0, 0)$, затем поднимется до $1$, опустится до $-1$, и снова вернется к 0 через $2\pi$.

2) Растяжение графика от оси $Oy$ с коэффициентом $k = 3$

При добавлении множителя $\frac{1}{3}$ в аргумент синуса, период изменяется:

$$T = 2\pi \times 3 = 6\pi.$$

Это растягивает график по оси $x$, и теперь каждый цикл будет занимать $6\pi$ единиц по оси $x$, что увеличивает расстояние между пиками и впадинами.

3) Перемещение на 2 единицы вниз вдоль оси ординат

Добавление $-2$ сдвигает график на 2 единицы вниз.

• Максимальное значение теперь будет равно $-1$ (раньше было $1$),
• Минимальное значение теперь будет равно $-3$ (раньше было $-1$).

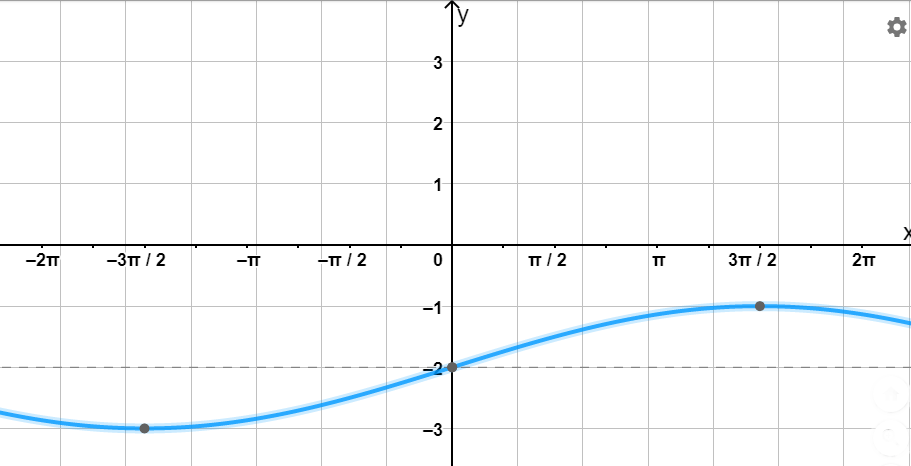
4) Достроим график функции

Теперь можем построить график функции $y = \sin \frac{x}{3} — 2$:

• Период функции $T = 6\pi$,
• Амплитуда $1$,
• График будет колебаться между $-3$ и $-1$, сдвинут вниз на 2 единицы.