ГДЗ по Алгебре 10 Класс Номер 18.8 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а) $y=\{\begin{array}{ll}\cos 2x,& \text{если }x\le \pi \\ -\frac{1}{2},& \text{если }x>\pi \end{array}$

б) $y=\{\begin{array}{ll}-\sin 3x,& \text{если }x<0\\ \sqrt{x},& \text{если }x\ge 0\end{array}$

В данной задаче $n$ — целое неотрицательное число;

а) $y = \begin{cases} \cos 2x, & \text{если } x \leq \pi \\ -\frac{1}{2}, & \text{если } x > \pi \end{cases};$

$y = \cos 2x$ — уравнение синусоиды:
$y(\pi) = \cos 2\pi = 1;$

$y = -\frac{1}{2}$ — уравнение прямой;

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty);$
• Множество значений: $E(f) = [-1; 1];$
• Возрастает на $\left[ \frac{\pi}{2} — 2\pi n; \pi — 2\pi n \right];$
• Убывает на $\left[ -2\pi n; \frac{\pi}{2} — 2\pi n \right];$
• Постоянна на $(\pi; +\infty);$
• $f(x) > 0$ на $\left( -\frac{\pi}{4} — 2\pi n; \frac{\pi}{4} — 2\pi n \right) \cup \left( \frac{3\pi}{4}; \pi \right);$
• $f(x) < 0$ на $\left( \frac{\pi}{4} — 2\pi n; \frac{3\pi}{4} — 2\pi n \right) \cup (\pi; +\infty);$
• Функция ни четная, ни нечетная;
• Функция не является периодической;

б) $y = \begin{cases} -\sin 3x, & \text{если } x < 0 \\ \sqrt{x}, & \text{если } x \geq 0 \end{cases};$

$y = -\sin 3x$ — уравнение синусоиды:
$y(0) = -\sin (3 \cdot 0) = -\sin 0 = 0;$

$y = \sqrt{x}$ — уравнение ветви параболы:
$x_0 = 0, \, y_0 = 0;$

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty);$
• Множество значений: $E(f) = [-1; +\infty);$
• Возрастает на $\left[ -\frac{\pi}{2} — 2\pi n; -\frac{\pi}{6} — 2\pi n \right] \cup [0; +\infty);$
• Убывает на $\left[ -\frac{5\pi}{6} — 2\pi n; -\frac{\pi}{2} — 2\pi n \right] \cup \left[ -\frac{\pi}{6}; 0 \right];$
• $f(x) > 0$ на $\left( -\frac{\pi}{3} — 2\pi n; -2\pi n \right) \cup (0; +\infty);$
• $f(x) < 0$ на $\left( -\frac{2\pi}{3} — 2\pi n; -\frac{\pi}{3} — 2\pi n \right);$
• Функция ни четная, ни нечетная;
• Функция не является периодической

а)

Рассмотрим функцию:

$$y = \begin{cases} \cos 2x, & \text{если } x \leq \pi \\ -\frac{1}{2}, & \text{если } x > \pi \end{cases}$$

1) Уравнение синусоиды:

Для первого случая $y = \cos 2x$ функция представляет собой синусоиду с амплитудой 1 и периодом $\frac{\pi}{2}$ (так как $\cos 2x$ — это косинус с удвоенной частотой).

• $y(\pi) = \cos(2 \cdot \pi) = \cos(2\pi) = 1$, то есть значение функции в точке $x = \pi$ равно 1.

2) Уравнение прямой:

Во втором случае $y = -\frac{1}{2}$ — это уравнение горизонтальной прямой, которая пересекает ось $y$ на уровне $-\frac{1}{2}$. Эта часть функции постоянна и не зависит от $x$, пока $x > \pi$.

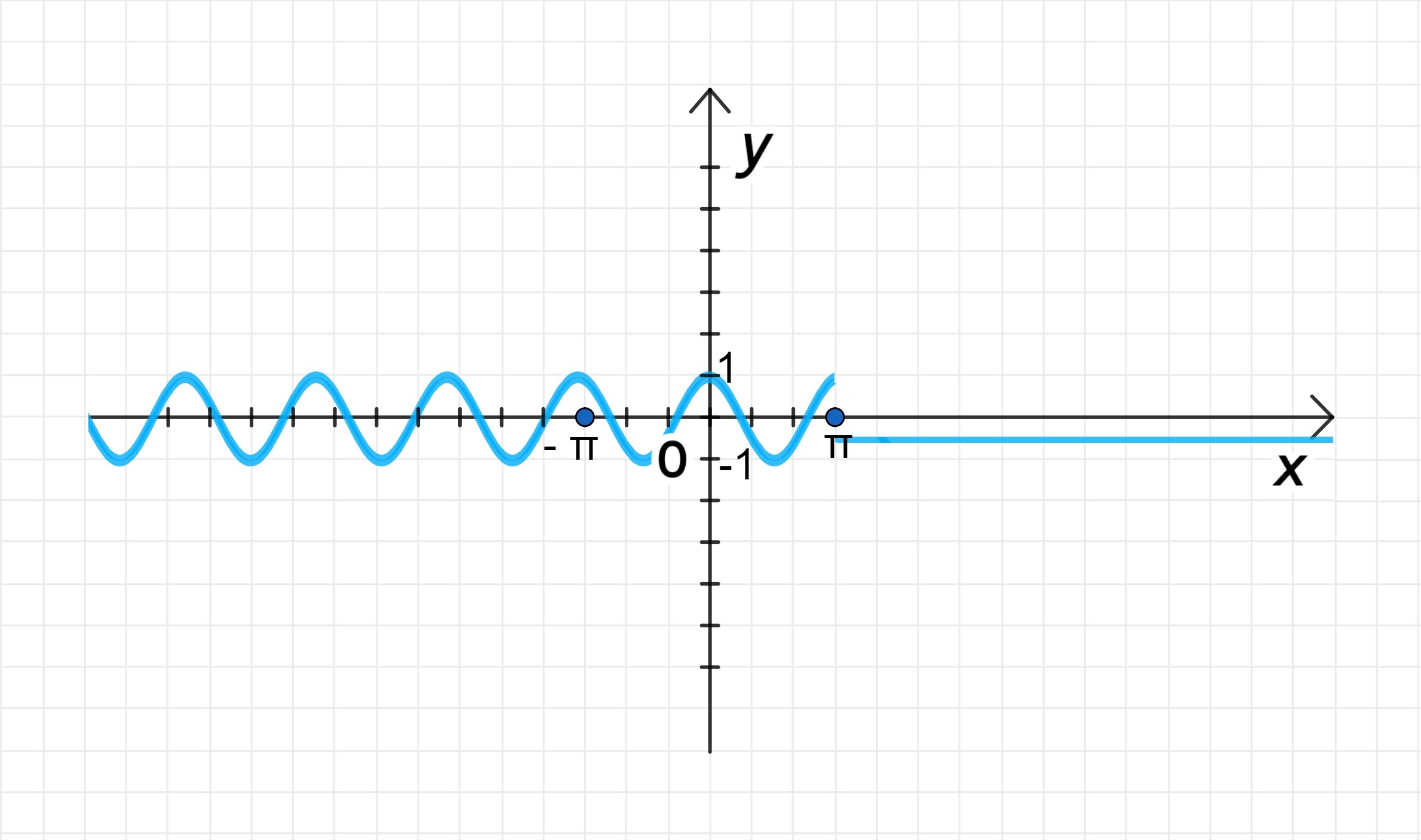
3) Графики функций:

Графики двух функций можно представить как график синусоиды на интервале $(-\infty, \pi]$ и горизонтальную прямую на интервале $(\pi, +\infty)$.

• Для синусоиды: начинается с $y = \cos(2x)$, что на интервале $x \leq \pi$ будет плавно изменяться в пределах от 1 до -1.
• Для прямой: после $\pi$ функция принимает значение $-\frac{1}{2}$ и остается постоянной.

4) Свойства функции:

• Область определения: так как синусоида $\cos 2x$ определена для всех $x$, а прямая $-\frac{1}{2}$ также определена для всех $x$, то область определения функции $D(f) = (-\infty; +\infty)$.
• Множество значений: синусоида $y = \cos 2x$ принимает значения от -1 до 1, а прямая $y = -\frac{1}{2}$ всегда равна $-\frac{1}{2}$, то есть множества значений функции будет $E(f) = [-1; 1]$.
• Возрастание: синусоида $\cos 2x$ возрастает на интервале, где производная $y’ = -2\sin 2x$ положительна, то есть на интервале $\left[ \frac{\pi}{2} — 2\pi n; \pi — 2\pi n \right]$, где $n$ — целое неотрицательное число.
• Убывание: синусоида убывает на интервале, где производная отрицательна, то есть на интервале $\left[ -2\pi n; \frac{\pi}{2} — 2\pi n \right]$.
• Постоянство: функция $y = -\frac{1}{2}$ является постоянной на интервале $(\pi; +\infty)$.
• Значения функции больше 0: функция $f(x) > 0$ на интервале $\left( -\frac{\pi}{4} — 2\pi n; \frac{\pi}{4} — 2\pi n \right) \cup \left( \frac{3\pi}{4}; \pi \right)$.
• Значения функции меньше 0: функция $f(x) < 0$ на интервале $\left( \frac{\pi}{4} — 2\pi n; \frac{3\pi}{4} — 2\pi n \right) \cup (\pi; +\infty)$.
• Четность/нечетность: функция не является четной или нечетной, так как $\cos 2x$ — четная, а $-\frac{1}{2}$ — постоянная, и комбинированная функция не имеет симметрии.
• Периодичность: функция не является периодической, поскольку имеет разрыв в точке $x = \pi$, где сменяется тип функции (синусоида на прямую).

б)

Рассмотрим функцию:

$$y = \begin{cases} -\sin 3x, & \text{если } x < 0 \\ \sqrt{x}, & \text{если } x \geq 0 \end{cases}$$

1) Уравнение синусоиды:

Для первого случая $y = -\sin 3x$, это уравнение синусоиды с амплитудой 1 и периодом $\frac{2\pi}{3}$ (так как $\sin 3x$ имеет удвоенную частоту по сравнению с обычной синусоидой).

• $y(0) = -\sin(3 \cdot 0) = -\sin(0) = 0$.

2) Уравнение ветви параболы:

Во втором случае $y = \sqrt{x}$ — это функция, которая определена только для $x \geq 0$. График будет представлять собой ветвь параболы, начинающуюся в точке $(0, 0)$.

• Для $x_0 = 0$, $y_0 = 0$.

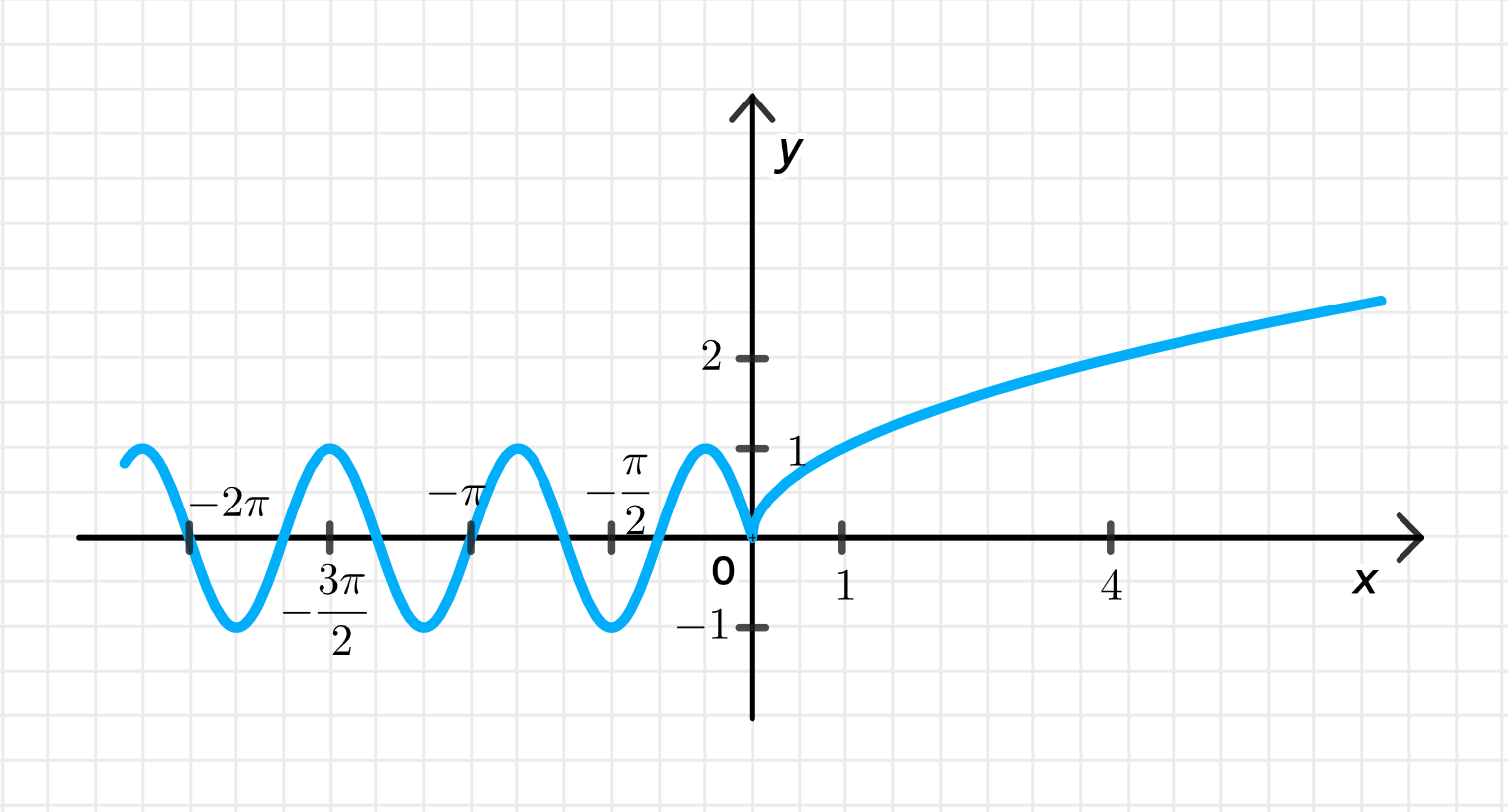
3) Графики функций:

Графики функций можно изобразить следующим образом:

• Для синусоиды на интервале $x < 0$ — функция будет колебаться от -1 до 1, а затем снова переходить через 0.
• Для корня $y = \sqrt{x}$ на интервале $x \geq 0$ график будет монотонно возрастать от 0 вверх.

4) Свойства функции:

• Область определения: синусоида $-\sin 3x$ определена для всех $x < 0$, а $\sqrt{x}$ определена только для $x \geq 0$, поэтому область определения функции будет $D(f) = (-\infty; +\infty)$.
• Множество значений: для синусоиды $-\sin 3x$ значения будут изменяться от -1 до 1, а для корня $\sqrt{x}$ значения будут больше или равны нулю, поэтому множество значений функции будет $E(f) = [-1; +\infty)$.
• Возрастание: на интервале $[0; +\infty)$ функция $\sqrt{x}$ возрастает, а синусоида возрастает на интервале $\left[ -\frac{\pi}{2} — 2\pi n; -\frac{\pi}{6} — 2\pi n \right]$.
• Убывание: на интервале $\left[ -\frac{5\pi}{6} — 2\pi n; -\frac{\pi}{2} — 2\pi n \right]$ синусоида убывает, а на интервале $\left[ -\frac{\pi}{6}; 0 \right]$ корень убывает.
• Значения функции больше 0: на интервале $(-\frac{\pi}{3} — 2\pi n; -2\pi n) \cup (0; +\infty)$ функция принимает положительные значения.
• Значения функции меньше 0: на интервале $(-\frac{2\pi}{3} — 2\pi n; -\frac{\pi}{3} — 2\pi n)$ функция принимает отрицательные значения.
• Четность/нечетность: функция не является четной или нечетной, так как синусоида и корень имеют разные симметрии.
• Периодичность: функция не является периодической, так как она имеет разрыв в точке $x = 0$, где сменяется тип функции (синусоида на корень).