ГДЗ по Алгебре 10 Класс Номер 18.9 Профильный Уровень Мордкович — Подробные Ответы

а) $y=\{\begin{array}{ll}-2\sin x,& \text{если }x<0\\ \sqrt{2x},& \text{если }x\ge 0\end{array}$

б) $y=\{\begin{array}{ll}\sqrt{-x},& \text{если }x<0\\ 3\cos x-3,& \text{если }x>0\end{array}$

В данной задаче $n$ — целое неотрицательное число;

а) $y = \begin{cases} -2 \sin x, & \text{если } x < 0 \\ \sqrt{2x}, & \text{если } x \geq 0 \end{cases};$

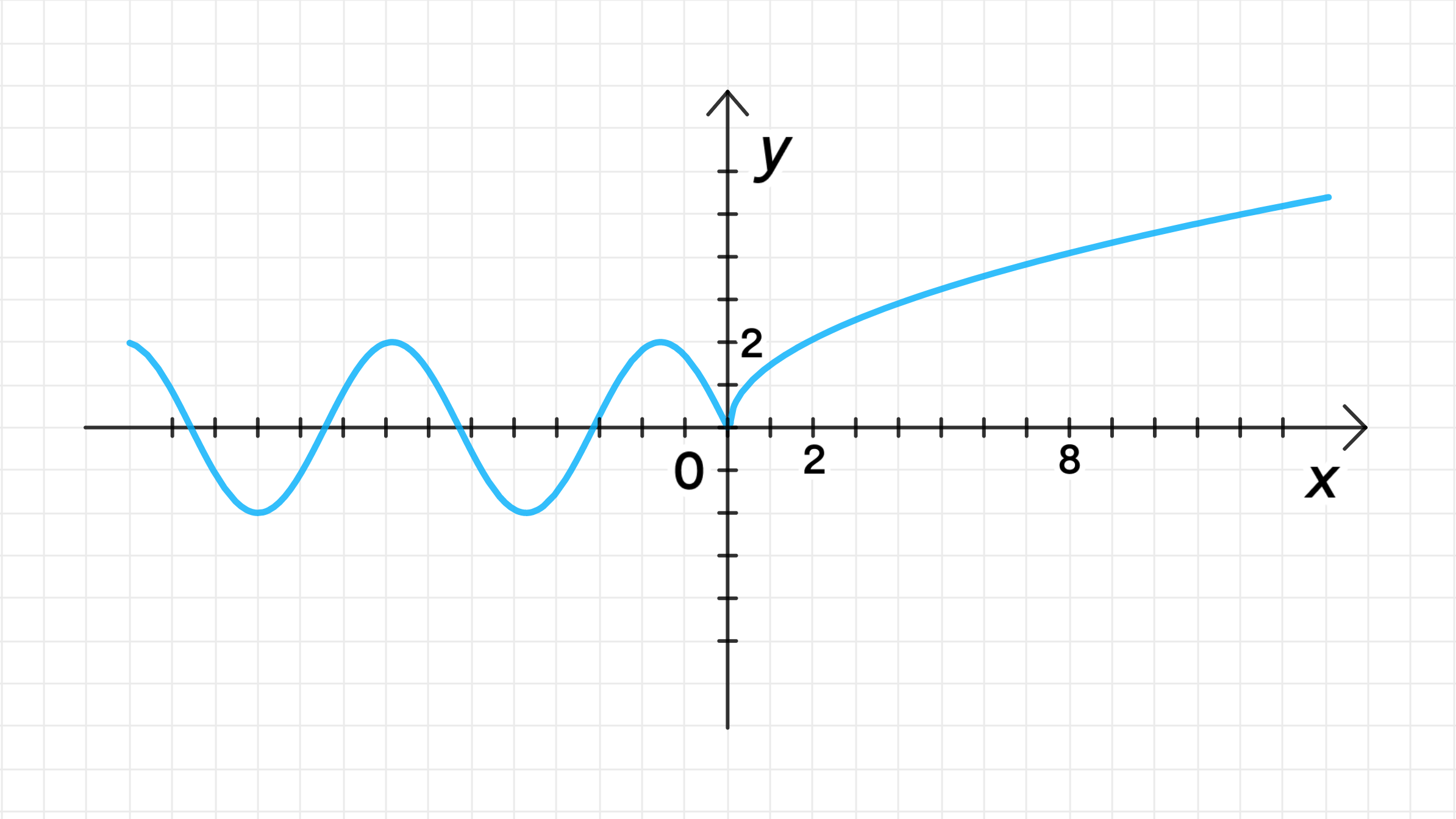
$y = -2 \sin x$ — уравнение синусоиды:
$y(0) = -2 \sin 0 = -2 \cdot 0 = 0;$

$y = \sqrt{2x}$ — уравнение ветви параболы:
$x_0 = 0, \, y_0 = 0;$

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty);$
• Множество значений: $E(f) = [-2; +\infty);$
• Возрастает на $\left[ -\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n \right] \cup [0; +\infty);$
• Убывает на $\left[ -\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n \right] \cup \left[ -\frac{\pi}{2}; 0 \right];$
• $f(x) \geq 0$ на $(-\pi — 2\pi n; -2\pi n) \cup (0; +\infty);$
• $f(x) < 0$ на $(-2\pi — 2\pi n; -\pi — 2\pi n);$
• Функция ни четная, ни нечетная;
• Функция не является периодической;

б) $y = \begin{cases} \sqrt{-x}, & \text{если } x < 0 \\ 3 \cos x — 3, & \text{если } x > 0 \end{cases};$

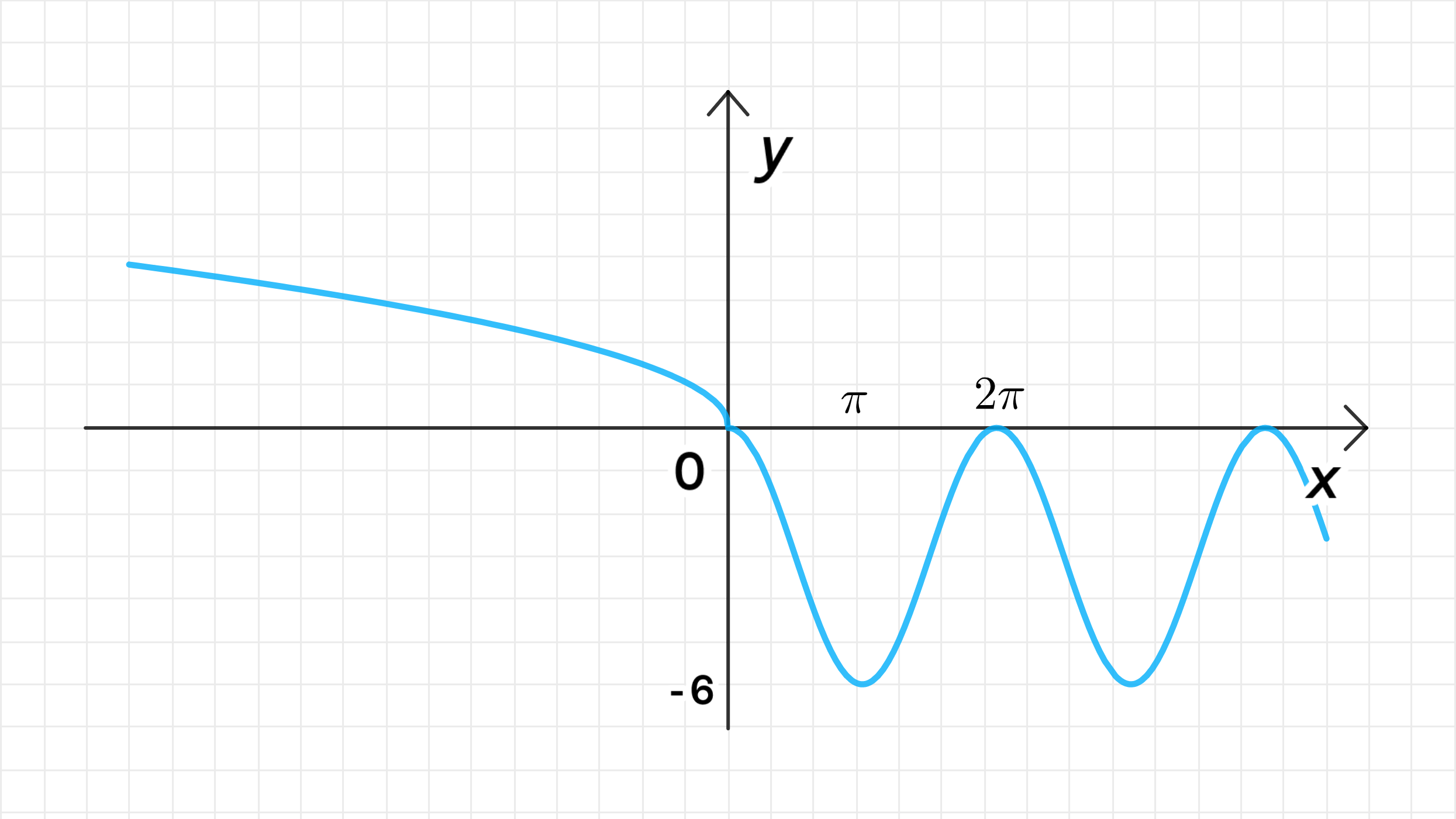
$y = 3 \cos x — 3$ — уравнение синусоиды:
$y(0) = 3 \cos 0 — 3 = 3 \cdot 1 — 3 = 0;$

$y = \sqrt{-x}$ — уравнение ветви параболы:
$x_0 = 0, \, y_0 = 0;$

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty);$
• Множество значений: $E(f) = [-6; +\infty);$
• Возрастает на $[\pi + 2\pi n; 2\pi + 2\pi n];$
• Убывает на $(-\infty; 0] \cup [2\pi n; \pi + 2\pi n];$
• $f(x) > 0$ на $(-\infty; 0);$
• $f(x) < 0$ на $(2\pi n; 2\pi + 2\pi n);$
• Функция ни четная, ни нечетная;
• Функция не является периодической

В данной задаче $n$ — целое неотрицательное число. Рассмотрим два случая функции $y$, каждый из которых представлен в виде кусочной функции.

а) Функция:

$$y = \begin{cases} -2 \sin x, & \text{если } x < 0 \\ \sqrt{2x}, & \text{если } x \geq 0 \end{cases}$$

1. Исследование функции $y = -2 \sin x$ при $x < 0$:

• Это уравнение синусоиды, где амплитуда равна $2$, и коэффициент перед синусом отрицательный. Таким образом, график будет зеркален относительно оси $x$.
• При $x = 0$:

  $$y(0) = -2 \sin 0 = -2 \cdot 0 = 0$$

  Значение функции в точке $x = 0$ равно $0$, так как синус от нуля равен нулю.

2. Исследование функции $y = \sqrt{2x}$ при $x \geq 0$:

• Это уравнение ветви параболы, поскольку оно является корнем из линейной функции.
• При $x = 0$:

  $$y(0) = \sqrt{2 \cdot 0} = \sqrt{0} = 0$$

  Значение функции в точке $x = 0$ также равно $0$.

• Теперь исследуем таблицу значений функции для разных $x$:

• Для $x = 2$, подставляем в уравнение:

  $$y(2) = \sqrt{2 \cdot 2} = \sqrt{4} = 2$$

• Для $x = 4.5$, подставляем в уравнение:

  $$y(4.5) = \sqrt{2 \cdot 4.5} = \sqrt{9} = 3$$

3. График функции:

• Для $x < 0$, график будет представлять собой отрицательную синусоиду, начиная с $x = 0$, и имеющую амплитуду $2$.
• Для $x \geq 0$, график будет представлять собой ветвь параболы, начиная с точки $(0, 0)$, и увеличивающуюся по мере роста $x$.

4. Свойства функции:

• Область определения:
  Рассмотрим области для каждой части функции.
  • Для $y = -2 \sin x$, область определения $x < 0$ — все значения $x$ от $-\infty$ до $0$.
  • Для $y = \sqrt{2x}$, область определения $x \geq 0$ — все значения $x$ от $0$ до $+\infty$.
    Таким образом, область определения функции:

  $$D(f) = (-\infty; +\infty)$$

• Множество значений:
  • Для $y = -2 \sin x$, значения функции колеблются в пределах $[-2, 2]$, но на интервале $(-\infty; 0)$ значения $y$ могут быть только от $-2$ до $0$.
  • Для $y = \sqrt{2x}$, функция возрастает и её минимальное значение на интервале $[0, +\infty)$ — это $0$, а максимальное стремится к $+\infty$.
    Таким образом, множество значений функции:

  $$E(f) = [-2; +\infty)$$

• Возрастание и убывание:
  • Функция $y = -2 \sin x$ возрастает на интервалах:

    $$\left[ -\frac{3\pi}{2} — 2\pi n; -\frac{\pi}{2} — 2\pi n \right] \cup [0; +\infty)$$

  • Функция $y = -2 \sin x$ убывает на интервалах:

    $$\left[ -\frac{5\pi}{2} — 2\pi n; -\frac{3\pi}{2} — 2\pi n \right] \cup \left[ -\frac{\pi}{2}; 0 \right]$$

  • Функция $y = \sqrt{2x}$ возрастает на интервале $[0; +\infty)$.
  • Функция $y = \sqrt{2x}$ убывает на $(-\infty; 0]$ (для $x$ отрицательных значений не существует, так что не рассматривается).
• Знаки функции:
  • $f(x) \geq 0$ на $(-\pi — 2\pi n; -2\pi n) \cup (0; +\infty)$
  • $f(x) < 0$ на $(-2\pi — 2\pi n; -\pi — 2\pi n)$
• Четность и периодичность:
  • Функция не является четной, так как она не симметрична относительно оси $y$.
  • Функция не является нечетной, так как для всех $x$, $f(x) \neq -f(-x)$.
  • Функция не является периодической, так как не существует постоянного периода для всей функции из-за её разрывов.

б) Функция:

$$y = \begin{cases} \sqrt{-x}, & \text{если } x < 0 \\ 3 \cos x — 3, & \text{если } x > 0 \end{cases}$$

1. Исследование функции $y = 3 \cos x — 3$ при $x > 0$:

• Это уравнение косинусоиды, с амплитудой $3$ и сдвигом на $-3$ вдоль оси $y$.
• При $x = 0$:

  $$y(0) = 3 \cos 0 — 3 = 3 \cdot 1 — 3 = 0$$

  Значение функции в точке $x = 0$ равно $0$.

2. Исследование функции $y = \sqrt{-x}$ при $x < 0$:

• Это уравнение ветви параболы, которая существует только для отрицательных значений $x$.
• При $x = 0$:

  $$y(0) = \sqrt{-0} = 0$$

• Теперь исследуем таблицу значений функции для разных $x$:

• Для $x = -1$, подставляем в уравнение:

  $$y(-1) = \sqrt{-(-1)} = \sqrt{1} = 1$$

• Для $x = -4$, подставляем в уравнение:

  $$y(-4) = \sqrt{-(-4)} = \sqrt{4} = 2$$

3. График функции:

• Для $x > 0$, график представляет собой косинусоиду с амплитудой 3 и сдвигом вниз на 3 единицы.
• Для $x < 0$, график представляет собой ветвь параболы.

4. Свойства функции:

• Область определения:
  Рассмотрим области для каждой части функции.
  • Для $y = 3 \cos x — 3$, область определения $x > 0$.
  • Для $y = \sqrt{-x}$, область определения $x < 0$.
    Таким образом, область определения функции:

  $$D(f) = (-\infty; +\infty)$$

• Множество значений:
  • Для $y = 3 \cos x — 3$, функция изменяет свои значения от $-6$ до $+\infty$, так как минимальное значение косинуса равно $-1$, а максимальное — $1$.
  • Для $y = \sqrt{-x}$, функция возрастает, начиная с $0$, и стремится к $+\infty$.
    Таким образом, множество значений функции:

  $$E(f) = [-6; +\infty)$$

• Возрастание и убывание:
  • Функция $y = 3 \cos x — 3$ возрастает на интервалах:

    $$[\pi + 2\pi n; 2\pi + 2\pi n]$$

  • Функция $y = 3 \cos x — 3$ убывает на интервалах:

    $$(-\infty; 0] \cup [2\pi n; \pi + 2\pi n]$$

• Знаки функции:
  • $f(x) > 0$ на $(-\infty; 0)$.
  • $f(x) < 0$ на $(2\pi n; 2\pi + 2\pi n)$.
• Четность и периодичность:
  • Функция не является четной, так как она не симметрична относительно оси $y$.
  • Функция не является нечетной, так как для всех $x$, $f(x) \neq -f(-x)$.
  • Функция не является периодической, так как не существует постоянного периода для всей функции из-за её разрывов.