ГДЗ по Алгебре 10 Класс Номер 19.1 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=3\sin (x+\frac{\pi }{2})$

б) $y=\cos \frac{1}{2}(x+\frac{\pi }{3})$

а) $y = 3 \sin \left( x + \frac{\pi}{2} \right)$

Нули функции:

$$\sin \left( x + \frac{\pi}{2} \right) = 0$$ $$x + \frac{\pi}{2} = \pi n$$ $$x = -\frac{\pi}{2} + \pi n$$ $$x_0 = -\frac{\pi}{2} + \pi \cdot 0 = -\frac{\pi}{2}$$ $$x_1 = -\frac{\pi}{2} + \pi = -\frac{\pi}{2} + \frac{2\pi}{2} = \frac{\pi}{2}$$

Середина дуги:

$$x = \frac{1}{2} \left( -\frac{\pi}{2} + \frac{\pi}{2} \right) = \frac{1}{2} \cdot 0 = 0$$ $$y = 3 \sin \left( 0 + \frac{\pi}{2} \right) = 3 \sin \frac{\pi}{2} = 3 \cdot 1 = 3$$

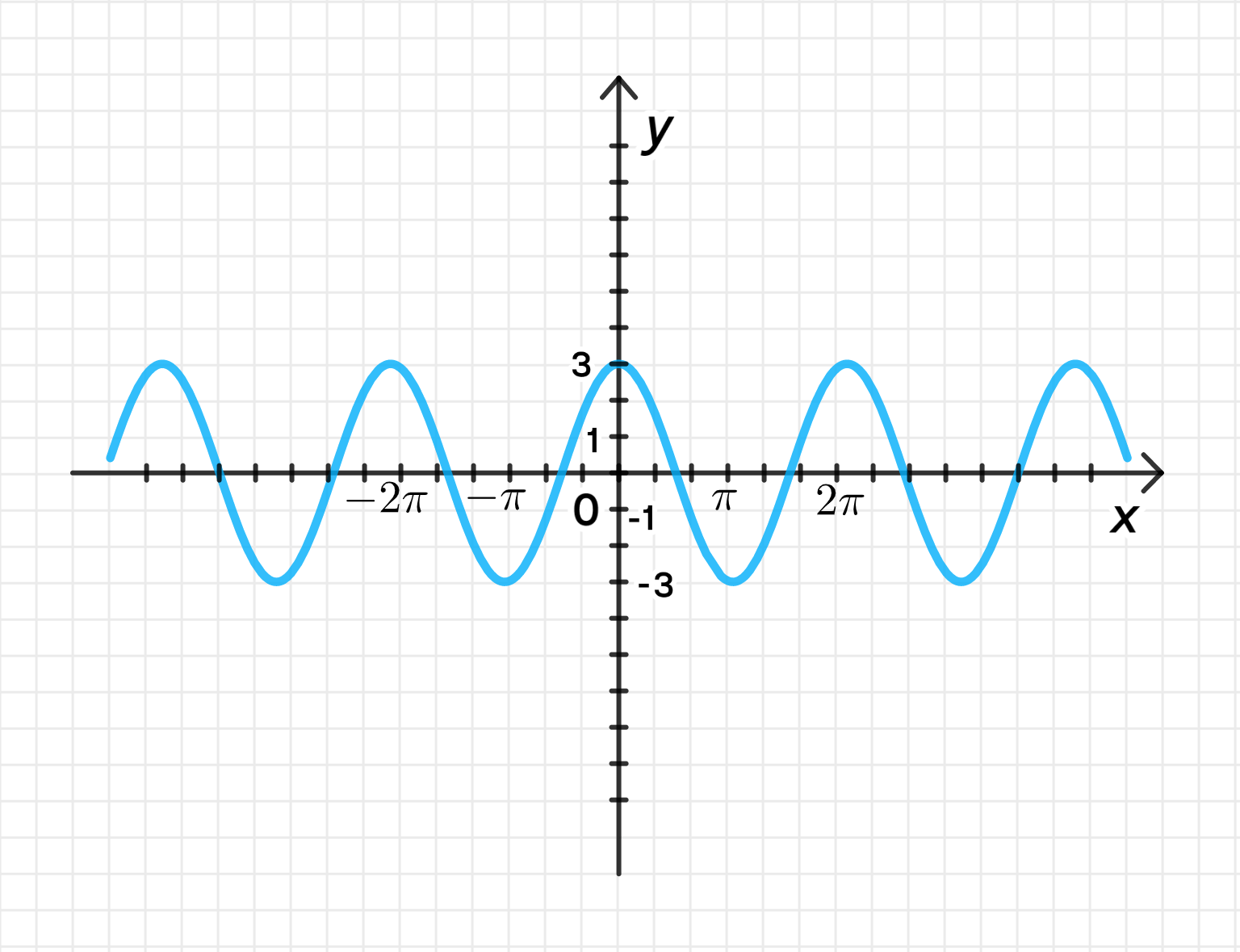
График функции:

б) $y = \cos \frac{1}{2} \left( x + \frac{\pi}{3} \right)$

Нули функции:

$$\cos \frac{1}{2} \left( x + \frac{\pi}{3} \right) = 0$$ $$\frac{1}{2} \left( x + \frac{\pi}{3} \right) = \pm \frac{\pi}{2} + 2\pi n$$ $$x + \frac{\pi}{3} = \pm \pi + 4\pi n$$ $$x_0 = -\frac{\pi}{3} — \pi = -\frac{\pi}{3} — \frac{3\pi}{3} = -\frac{4\pi}{3}$$ $$x_1 = -\frac{\pi}{3} + \pi = -\frac{\pi}{3} + \frac{3\pi}{3} = \frac{2\pi}{3}$$

Середина дуги:

$$x = \frac{1}{2} \left( -\frac{4\pi}{3} + \frac{2\pi}{3} \right) = \frac{1}{2} \cdot \left( -\frac{2\pi}{3} \right) = -\frac{\pi}{3}$$ $$y = \cos \frac{1}{2} \left( -\frac{\pi}{3} + \frac{\pi}{3} \right) = \cos \left( \frac{1}{2} \cdot 0 \right) = \cos 0 = 1$$

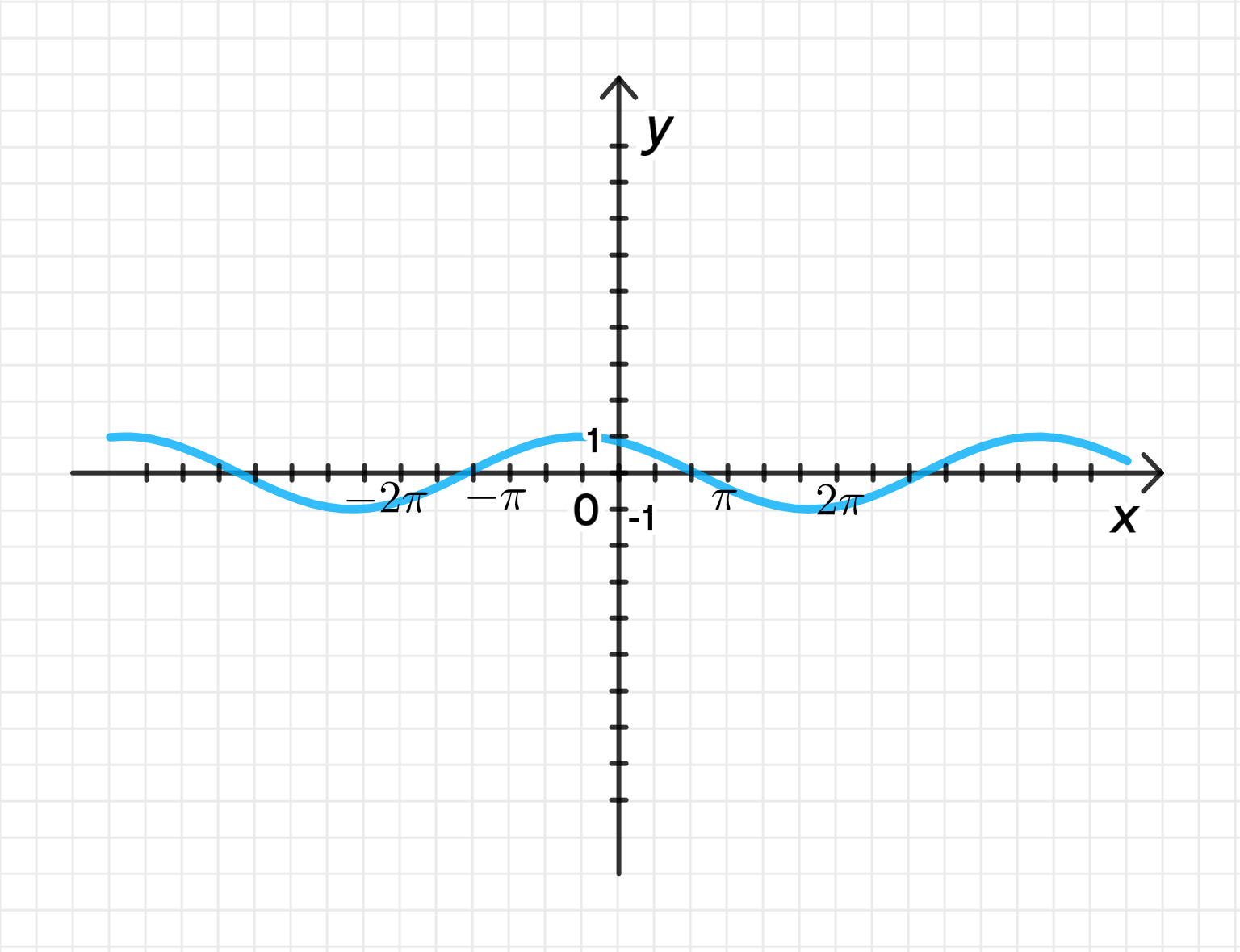
График функции:

а) $y = 3 \sin \left( x + \frac{\pi}{2} \right)$

1) Нули функции

Нули функции $y = 3 \sin \left( x + \frac{\pi}{2} \right)$ — это значения $x$, при которых $y = 0$. Для того чтобы найти нули, приравняем синус к нулю:

$$\sin \left( x + \frac{\pi}{2} \right) = 0$$

Синус равен нулю, когда его аргумент равен целому числу $\pi$, то есть:

$$x + \frac{\pi}{2} = \pi n, \quad n \in \mathbb{Z}$$

Теперь решим это уравнение относительно $x$:

$$x = -\frac{\pi}{2} + \pi n$$

Таким образом, нули функции — это значения $x = -\frac{\pi}{2} + \pi n$, где $n$ — целое число.

Рассмотрим несколько первых значений $n$:

• Для $n = 0$, получаем $x_0 = -\frac{\pi}{2}$.
• Для $n = 1$, получаем $x_1 = -\frac{\pi}{2} + \pi = \frac{\pi}{2}$.

Таким образом, два ближайших нуля функции находятся в точках:

$$x_0 = -\frac{\pi}{2}, \quad x_1 = \frac{\pi}{2}$$

2) Середина дуги

Середина дуги — это значение $x$, где функция достигает максимума или минимума, то есть значение функции равно максимальному или минимальному значению синуса. В данном случае амплитуда функции равна 3, так как перед синусом стоит множитель 3. Мы ищем точку, в которой функция будет равна 3 (максимум).

Сначала найдем среднее значение между ближайшими нулями $x_0 = -\frac{\pi}{2}$ и $x_1 = \frac{\pi}{2}$. Для этого вычислим:

$$x = \frac{1}{2} \left( x_0 + x_1 \right) = \frac{1}{2} \left( -\frac{\pi}{2} + \frac{\pi}{2} \right) = 0$$

Таким образом, середина дуги находится в точке $x = 0$.

Теперь подставим это значение в исходное уравнение для функции:

$$y = 3 \sin \left( 0 + \frac{\pi}{2} \right) = 3 \sin \frac{\pi}{2} = 3 \cdot 1 = 3$$

Таким образом, в точке $x = 0$ функция достигает значения 3, что является максимумом функции.

3) График функции

График функции $y = 3 \sin \left( x + \frac{\pi}{2} \right)$ представляет собой синусоиду с амплитудой 3, которая сдвинута на $-\frac{\pi}{2}$ по оси $x$. Период этой функции равен $2\pi$, так как коэффициент перед $x$ равен 1.

• Нули функции находятся в точках $x_0 = -\frac{\pi}{2}$ и $x_1 = \frac{\pi}{2}$.
• Середина дуги (максимум) находится в точке $x = 0$, где функция принимает значение 3.

б) $y = \cos \frac{1}{2} \left( x + \frac{\pi}{3} \right)$

1) Нули функции

Нули функции $y = \cos \frac{1}{2} \left( x + \frac{\pi}{3} \right)$ — это значения $x$, при которых $y = 0$. Для этого приравняем косинус к нулю:

$$\cos \frac{1}{2} \left( x + \frac{\pi}{3} \right) = 0$$

Косинус равен нулю, когда его аргумент равен $\frac{\pi}{2} + \pi n$, где $n$ — целое число. Таким образом, получаем уравнение:

$$\frac{1}{2} \left( x + \frac{\pi}{3} \right) = \frac{\pi}{2} + \pi n$$

Умножаем обе части на 2:

$$x + \frac{\pi}{3} = \pi + 2\pi n$$

Теперь решим относительно $x$:

$$x = \pi + 2\pi n — \frac{\pi}{3} = \frac{3\pi}{3} + \frac{6\pi n}{3} — \frac{\pi}{3} = \frac{2\pi}{3} + 2\pi n$$

Таким образом, нули функции — это значения $x = \frac{2\pi}{3} + 2\pi n$, где $n$ — целое число.

Рассмотрим несколько первых значений $n$:

• Для $n = 0$, получаем $x_0 = \frac{2\pi}{3}$.
• Для $n = -1$, получаем $x_1 = \frac{2\pi}{3} — 2\pi = -\frac{4\pi}{3}$.

Таким образом, два ближайших нуля функции находятся в точках:

$$x_0 = \frac{2\pi}{3}, \quad x_1 = -\frac{4\pi}{3}$$

2) Середина дуги

Середина дуги — это значение $x$, где функция достигает максимума или минимума. В данном случае амплитуда функции равна 1, так как перед косинусом нет множителя. Мы ищем точку, в которой функция будет равна 1 (максимум).

Сначала найдем среднее значение между ближайшими нулями $x_0 = \frac{2\pi}{3}$ и $x_1 = -\frac{4\pi}{3}$. Для этого вычислим:

$$x = \frac{1}{2} \left( x_0 + x_1 \right) = \frac{1}{2} \left( \frac{2\pi}{3} + \left(-\frac{4\pi}{3}\right) \right) = \frac{1}{2} \left( -\frac{2\pi}{3} \right) = -\frac{\pi}{3}$$

Таким образом, середина дуги находится в точке $x = -\frac{\pi}{3}$.

Теперь подставим это значение в исходное уравнение для функции:

$$y = \cos \frac{1}{2} \left( -\frac{\pi}{3} + \frac{\pi}{3} \right) = \cos \left( \frac{1}{2} \cdot 0 \right) = \cos 0 = 1$$

Таким образом, в точке $x = -\frac{\pi}{3}$ функция достигает значения 1, что является максимумом функции.

3) График функции

График функции $y = \cos \frac{1}{2} \left( x + \frac{\pi}{3} \right)$ представляет собой косинусоиду с амплитудой 1, которая сдвинута на $-\frac{\pi}{3}$ по оси $x$. Период этой функции равен $4\pi$, так как коэффициент перед $x$ равен $\frac{1}{2}$.

• Нули функции находятся в точках $x_0 = \frac{2\pi}{3}$ и $x_1 = -\frac{4\pi}{3}$.
• Середина дуги (максимум) находится в точке $x = -\frac{\pi}{3}$, где функция принимает значение 1.