ГДЗ по Алгебре 10 Класс Номер 19.2 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=-2\cos 2(x+\frac{\pi }{3});$

б) $y=-2\sin 3(x+\frac{\pi }{2})$

а) $y = -2 \cos 2\left(x + \frac{\pi}{3}\right);$

Нули функции:

$$\cos 2\left(x + \frac{\pi}{3}\right) = 0;$$ $$2\left(x + \frac{\pi}{3}\right) = \pm \frac{\pi}{2} + 2\pi n;$$ $$x + \frac{\pi}{3} = \pm \frac{\pi}{4} + \pi n;$$ $$x_0 = -\frac{\pi}{3} — \frac{\pi}{4} = -\frac{4\pi}{12} — \frac{3\pi}{12} = -\frac{7\pi}{12};$$ $$x_1 = -\frac{\pi}{3} + \frac{\pi}{4} = -\frac{4\pi}{12} + \frac{3\pi}{12} = -\frac{\pi}{12};$$

Середина дуги:

$$x = \frac{1}{2}\left(-\frac{7\pi}{12} — \frac{\pi}{12}\right) = \frac{1}{2} \cdot \left(-\frac{2\pi}{3}\right) = -\frac{\pi}{3};$$ $$y = -2 \cos 2\left(-\frac{\pi}{3} + \frac{\pi}{3}\right) = -2 \cos 0 = -2;$$

График функции:

б) $y = -2 \sin 3\left(x + \frac{\pi}{2}\right);$

Нули функции:

$$\sin 3\left(x + \frac{\pi}{2}\right) = 0;$$ $$3\left(x + \frac{\pi}{2}\right) = \pi n;$$ $$x + \frac{\pi}{2} = \frac{\pi n}{3};$$ $$x = -\frac{\pi}{2} + \frac{\pi n}{3};$$ $$x_0 = -\frac{\pi}{2} + \frac{\pi}{3} \cdot 0 = -\frac{\pi}{2};$$ $$x_1 = -\frac{\pi}{2} + \frac{\pi}{3} = -\frac{3\pi}{6} + \frac{2\pi}{6} = -\frac{\pi}{6};$$

Середина дуги:

$$x = \frac{1}{2}\left(-\frac{\pi}{2} — \frac{\pi}{6}\right) = \frac{1}{2} \cdot \left(-\frac{4\pi}{6}\right) = -\frac{4\pi}{12} = -\frac{\pi}{3};$$ $$y = -2 \sin 3\left(-\frac{\pi}{3} + \frac{\pi}{2}\right) = -2 \sin \frac{3\pi}{6} = -2 \sin \frac{\pi}{2} = -2;$$

График функции:

а) $y = -2 \cos 2\left(x + \frac{\pi}{3}\right);$

1) Нули функции

Для нахождения нулей функции, нам нужно приравнять выражение $y = -2 \cos 2\left(x + \frac{\pi}{3}\right)$ к нулю:

$$-2 \cos 2\left(x + \frac{\pi}{3}\right) = 0$$

Так как множитель $-2$ не равен нулю, это уравнение будет равно нулю тогда, когда $\cos 2\left(x + \frac{\pi}{3}\right) = 0$.

Косинус равен нулю, когда его аргумент равен $\frac{\pi}{2} + \pi n$, где $n$ — целое число. Таким образом, у нас получается:

$$2 \left( x + \frac{\pi}{3} \right) = \frac{\pi}{2} + \pi n$$

Решим это уравнение относительно $x$:

$$x + \frac{\pi}{3} = \frac{\pi}{4} + \pi n \quad \text{или} \quad x + \frac{\pi}{3} = -\frac{\pi}{4} + \pi n$$

Для первого случая:

$$x = -\frac{\pi}{3} + \frac{\pi}{4} + \pi n = -\frac{4\pi}{12} + \frac{3\pi}{12} + \pi n = -\frac{7\pi}{12} + \pi n$$

Для второго случая:

$$x = -\frac{\pi}{3} — \frac{\pi}{4} + \pi n = -\frac{4\pi}{12} — \frac{3\pi}{12} + \pi n = -\frac{7\pi}{12} + \pi n$$

Рассмотрим два ближайших значения $n = 0$ и $n = 1$:

Для $n = 0$:

$$x_0 = -\frac{7\pi}{12}$$

Для $n = 1$:

$$x_1 = -\frac{7\pi}{12} + \pi = -\frac{7\pi}{12} + \frac{12\pi}{12} = \frac{5\pi}{12}$$

Таким образом, два ближайших нуля функции:

$$x_0 = -\frac{7\pi}{12}, \quad x_1 = \frac{5\pi}{12}$$

2) Середина дуги

Середина дуги функции — это точка, в которой функция достигает максимума или минимума. В данном случае амплитуда функции равна $2$, так как перед косинусом стоит множитель $-2$. Чтобы найти середину дуги, найдем значение $x$, которое лежит между ближайшими нулями, и вычислим значение функции в этой точке.

Сначала находим середину между ближайшими нулями $x_0 = -\frac{7\pi}{12}$ и $x_1 = \frac{5\pi}{12}$:

$$x = \frac{1}{2}\left( x_0 + x_1 \right) = \frac{1}{2} \left( -\frac{7\pi}{12} + \frac{5\pi}{12} \right) = \frac{1}{2} \left( -\frac{2\pi}{12} \right) = -\frac{\pi}{12}$$

Теперь подставим это значение в исходную функцию:

$$y = -2 \cos 2\left( -\frac{\pi}{12} + \frac{\pi}{3} \right)$$

Приводим $\frac{\pi}{3}$ к общему знаменателю:

$$y = -2 \cos 2\left( -\frac{\pi}{12} + \frac{4\pi}{12} \right) = -2 \cos 2\left( \frac{3\pi}{12} \right) = -2 \cos \frac{\pi}{6}$$

Значение $\cos \frac{\pi}{6} = \frac{\sqrt{3}}{2}$, поэтому:

$$y = -2 \cdot \frac{\sqrt{3}}{2} = -\sqrt{3}$$

Таким образом, в середине дуги, когда $x = -\frac{\pi}{12}$, функция принимает значение $y = -\sqrt{3}$.

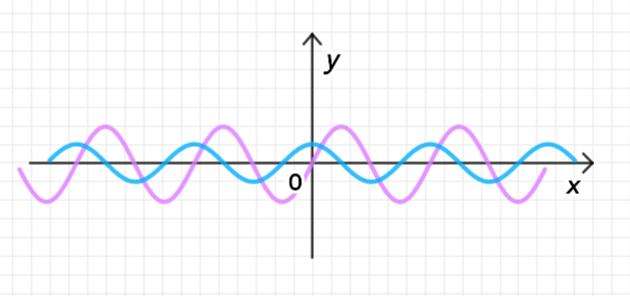
3) График функции

График функции $y = -2 \cos 2\left(x + \frac{\pi}{3}\right)$ представляет собой косинусоиду с амплитудой 2, сдвинутую по оси $x$ на $-\frac{\pi}{3}$, и с периодом, уменьшенным в 2 раза, поскольку коэффициент перед $x$ равен 2.

• Нули функции: $x_0 = -\frac{7\pi}{12}$, $x_1 = \frac{5\pi}{12}$.
• Середина дуги: $x = -\frac{\pi}{12}$, $y = -\sqrt{3}$.

б) $y = -2 \sin 3\left(x + \frac{\pi}{2}\right);$

1) Нули функции

Для нахождения нулей функции $y = -2 \sin 3\left(x + \frac{\pi}{2}\right)$, приравняем её к нулю:

$$-2 \sin 3\left(x + \frac{\pi}{2}\right) = 0$$

Так как множитель $-2$ не равен нулю, это уравнение будет равно нулю, когда:

$$\sin 3\left(x + \frac{\pi}{2}\right) = 0$$

Синус равен нулю, когда его аргумент равен $\pi n$, где $n$ — целое число. Таким образом, получаем уравнение:

$$3 \left( x + \frac{\pi}{2} \right) = \pi n$$

Решим относительно $x$:

$$x + \frac{\pi}{2} = \frac{\pi n}{3}$$ $$x = -\frac{\pi}{2} + \frac{\pi n}{3}$$

Для нескольких значений $n$:

• Для $n = 0$:

  $$x_0 = -\frac{\pi}{2} + \frac{\pi}{3} \cdot 0 = -\frac{\pi}{2}$$

• Для $n = 1$:

  $$x_1 = -\frac{\pi}{2} + \frac{\pi}{3} = -\frac{3\pi}{6} + \frac{2\pi}{6} = -\frac{\pi}{6}$$

Таким образом, два ближайших нуля функции:

$$x_0 = -\frac{\pi}{2}, \quad x_1 = -\frac{\pi}{6}$$

2) Середина дуги

Середина дуги — это точка, в которой функция достигает максимума или минимума. В данном случае амплитуда функции равна $2$, так как перед синусом стоит множитель $-2$. Для поиска середины дуги найдем значение $x$, которое лежит между ближайшими нулями, и вычислим значение функции в этой точке.

Найдем середину между ближайшими нулями $x_0 = -\frac{\pi}{2}$ и $x_1 = -\frac{\pi}{6}$:

$$x = \frac{1}{2} \left( x_0 + x_1 \right) = \frac{1}{2} \left( -\frac{\pi}{2} — \frac{\pi}{6} \right) = \frac{1}{2} \left( -\frac{3\pi}{6} — \frac{\pi}{6} \right) = -\frac{2\pi}{6} = -\frac{\pi}{3}$$

Теперь подставим это значение в исходную функцию:

$$y = -2 \sin 3\left( -\frac{\pi}{3} + \frac{\pi}{2} \right) = -2 \sin \frac{3\pi}{6} = -2 \sin \frac{\pi}{2} = -2$$

Таким образом, в середине дуги, когда $x = -\frac{\pi}{3}$, функция принимает значение $y = -2$.

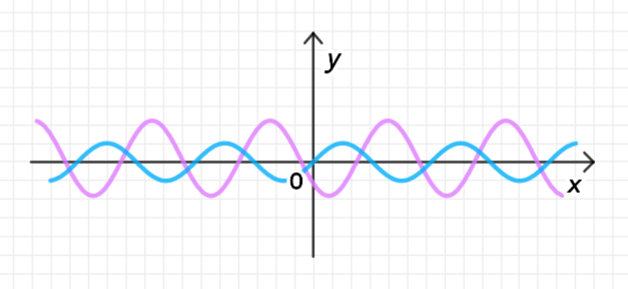
3) График функции

График функции $y = -2 \sin 3\left(x + \frac{\pi}{2}\right)$ представляет собой синусоиду с амплитудой 2, сдвинутую по оси $x$ на $-\frac{\pi}{2}$, и с периодом, уменьшенным в 3 раза, поскольку коэффициент перед $x$ равен 3.

• Нули функции: $x_0 = -\frac{\pi}{2}$, $x_1 = -\frac{\pi}{6}$.
• Середина дуги: $x = -\frac{\pi}{3}$, $y = -2$.