ГДЗ по Алгебре 10 Класс Номер 19.4 Профильный Уровень Мордкович — Подробные Ответы

а) $y=\frac{1}{2}\sin (\frac{x}{2}+\frac{\pi }{6});$

б) $y=-\frac{3}{2}\cos (\frac{x}{2}-\frac{\pi }{3})$$$

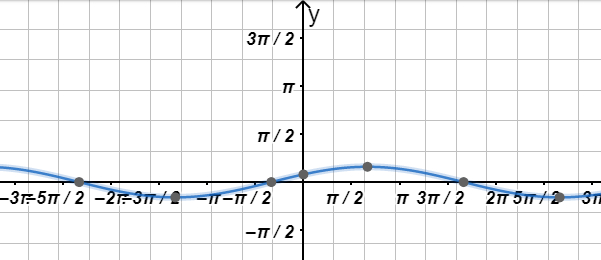
а) $y = \frac{1}{2} \sin \left( \frac{x}{2} + \frac{\pi}{6} \right);$

Нули функции:

$$\sin \left( \frac{x}{2} + \frac{\pi}{6} \right) = 0;$$ $$\frac{x}{2} + \frac{\pi}{6} = \pi n;$$ $$x + \frac{\pi}{3} = 2\pi n;$$ $$x = -\frac{\pi}{3} + 2\pi n;$$ $$x_0 = -\frac{\pi}{3} + 2\pi \cdot 0 = -\frac{\pi}{3};$$ $$x_1 = -\frac{\pi}{3} + 2\pi = -\frac{\pi}{3} + \frac{6\pi}{3} = \frac{5\pi}{3};$$

Середина дуги:

$$x = \frac{1}{2} \left( -\frac{\pi}{3} + \frac{5\pi}{3} \right) = \frac{1}{2} \cdot \frac{4\pi}{3} = \frac{2\pi}{3};$$ $$y = \frac{1}{2} \sin \left( \frac{2\pi}{6} + \frac{\pi}{6} \right) = \frac{1}{2} \sin \frac{\pi}{2} = \frac{1}{2};$$

График функции:

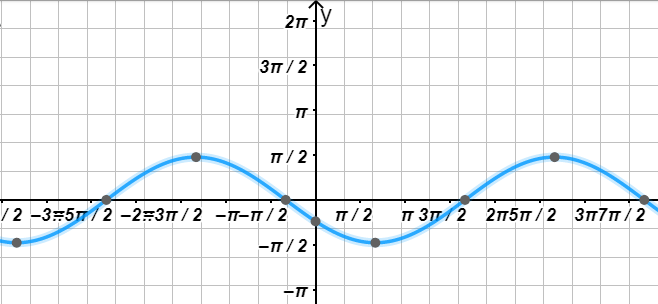
б) $y = -\frac{3}{2} \cos \left( \frac{x}{2} — \frac{\pi}{3} \right);$

Нули функции:

$$\cos \left( \frac{x}{2} — \frac{\pi}{3} \right) = 0;$$ $$\frac{x}{2} — \frac{\pi}{3} = \pm \frac{\pi}{2} + 2\pi n;$$ $$x — \frac{2\pi}{3} = \pm \pi + 4\pi n;$$ $$x_0 = \frac{2\pi}{3} — \pi = \frac{2\pi}{3} — \frac{3\pi}{3} = -\frac{\pi}{3};$$ $$x_1 = \frac{2\pi}{3} + \pi = \frac{2\pi}{3} + \frac{3\pi}{3} = \frac{5\pi}{3};$$

Середина дуги:

$$x = \frac{1}{2} \left( -\frac{\pi}{3} + \frac{5\pi}{3} \right) = \frac{1}{2} \cdot \frac{4\pi}{3} = \frac{2\pi}{3};$$ $$y = -\frac{3}{2} \cos \left( \frac{\pi}{3} — \frac{\pi}{3} \right) = -\frac{3}{2} \cos 0 = -\frac{3}{2};$$

График функции:

а) $y = \frac{1}{2} \sin \left( \frac{x}{2} + \frac{\pi}{6} \right)$

1) Нули функции:

Для того чтобы найти нули функции, необходимо решить уравнение, при котором синус принимает значение 0:

$$\sin \left( \frac{x}{2} + \frac{\pi}{6} \right) = 0.$$

Решение синуса равно нулю при $\frac{x}{2} + \frac{\pi}{6} = \pi n$, где $n$ — целое число. Переходим к решению для $x$:

$$\frac{x}{2} + \frac{\pi}{6} = \pi n \quad \Rightarrow \quad \frac{x}{2} = \pi n — \frac{\pi}{6} \quad \Rightarrow \quad x = 2\pi n — \frac{\pi}{3}.$$

Таким образом, нули функции можно записать как:

$$x = -\frac{\pi}{3} + 2\pi n.$$

Найдем первые два нуля функции, подставив $n = 0$ и $n = 1$:

• Для $n = 0$:

  $$x_0 = -\frac{\pi}{3} + 2\pi \cdot 0 = -\frac{\pi}{3}.$$

• Для $n = 1$:

  $$x_1 = -\frac{\pi}{3} + 2\pi = \frac{5\pi}{3}.$$

2) Середина дуги:

Середина дуги находится между двумя последовательными нулями функции. Для этого находим точку, которая будет посередине между $x_0 = -\frac{\pi}{3}$ и $x_1 = \frac{5\pi}{3}$:

$$x = \frac{1}{2} \left( -\frac{\pi}{3} + \frac{5\pi}{3} \right) = \frac{1}{2} \cdot \frac{4\pi}{3} = \frac{2\pi}{3}.$$

Теперь подставим значение $x = \frac{2\pi}{3}$ в исходную функцию, чтобы найти соответствующее значение $y$:

$$y = \frac{1}{2} \sin \left( \frac{\frac{2\pi}{3}}{2} + \frac{\pi}{6} \right) = \frac{1}{2} \sin \left( \frac{\pi}{3} + \frac{\pi}{6} \right) = \frac{1}{2} \sin \left( \frac{\pi}{2} \right).$$

Так как $\sin \left( \frac{\pi}{2} \right) = 1$, получаем:

$$y = \frac{1}{2} \cdot 1 = \frac{1}{2}.$$

3) График функции:

б) $y = -\frac{3}{2} \cos \left( \frac{x}{2} — \frac{\pi}{3} \right)$

1) Нули функции:

Для нахождения нулей функции нужно решить уравнение:

$$\cos \left( \frac{x}{2} — \frac{\pi}{3} \right) = 0.$$

Косинус равен нулю при $\frac{x}{2} — \frac{\pi}{3} = \pm \frac{\pi}{2} + 2\pi n$. Переходим к решению для $x$:

$$\frac{x}{2} — \frac{\pi}{3} = \pm \frac{\pi}{2} + 2\pi n \quad \Rightarrow \quad \frac{x}{2} = \frac{\pi}{3} \pm \frac{\pi}{2} + 2\pi n.$$

Умножим на 2:

$$x = 2\left( \frac{\pi}{3} \pm \frac{\pi}{2} + 2\pi n \right) = \frac{2\pi}{3} \pm \pi + 4\pi n.$$

Теперь найдем первые два нуля функции, подставив $n = 0$ и $n = 1$:

• Для $n = 0$ и $\frac{x}{2} — \frac{\pi}{3} = \frac{\pi}{2}$:

  $$x_0 = \frac{2\pi}{3} — \pi = -\frac{\pi}{3}.$$

• Для $n = 0$ и $\frac{x}{2} — \frac{\pi}{3} = -\frac{\pi}{2}$:

  $$x_1 = \frac{2\pi}{3} + \pi = \frac{5\pi}{3}.$$

2) Середина дуги:

Середина дуги между нулями находится точно так же, как и в предыдущем случае:

$$x = \frac{1}{2} \left( -\frac{\pi}{3} + \frac{5\pi}{3} \right) = \frac{1}{2} \cdot \frac{4\pi}{3} = \frac{2\pi}{3}.$$

Теперь подставим значение $x = \frac{2\pi}{3}$ в исходную функцию:

$$y = -\frac{3}{2} \cos \left( \frac{\frac{2\pi}{3}}{2} — \frac{\pi}{3} \right) = -\frac{3}{2} \cos \left( \frac{\pi}{3} — \frac{\pi}{3} \right) = -\frac{3}{2} \cos 0.$$

Так как $\cos 0 = 1$, получаем:

$$y = -\frac{3}{2} \cdot 1 = -\frac{3}{2}.$$

3) График функции: