ГДЗ по Алгебре 10 Класс Номер 20.18 Профильный Уровень Мордкович — Подробные Ответы

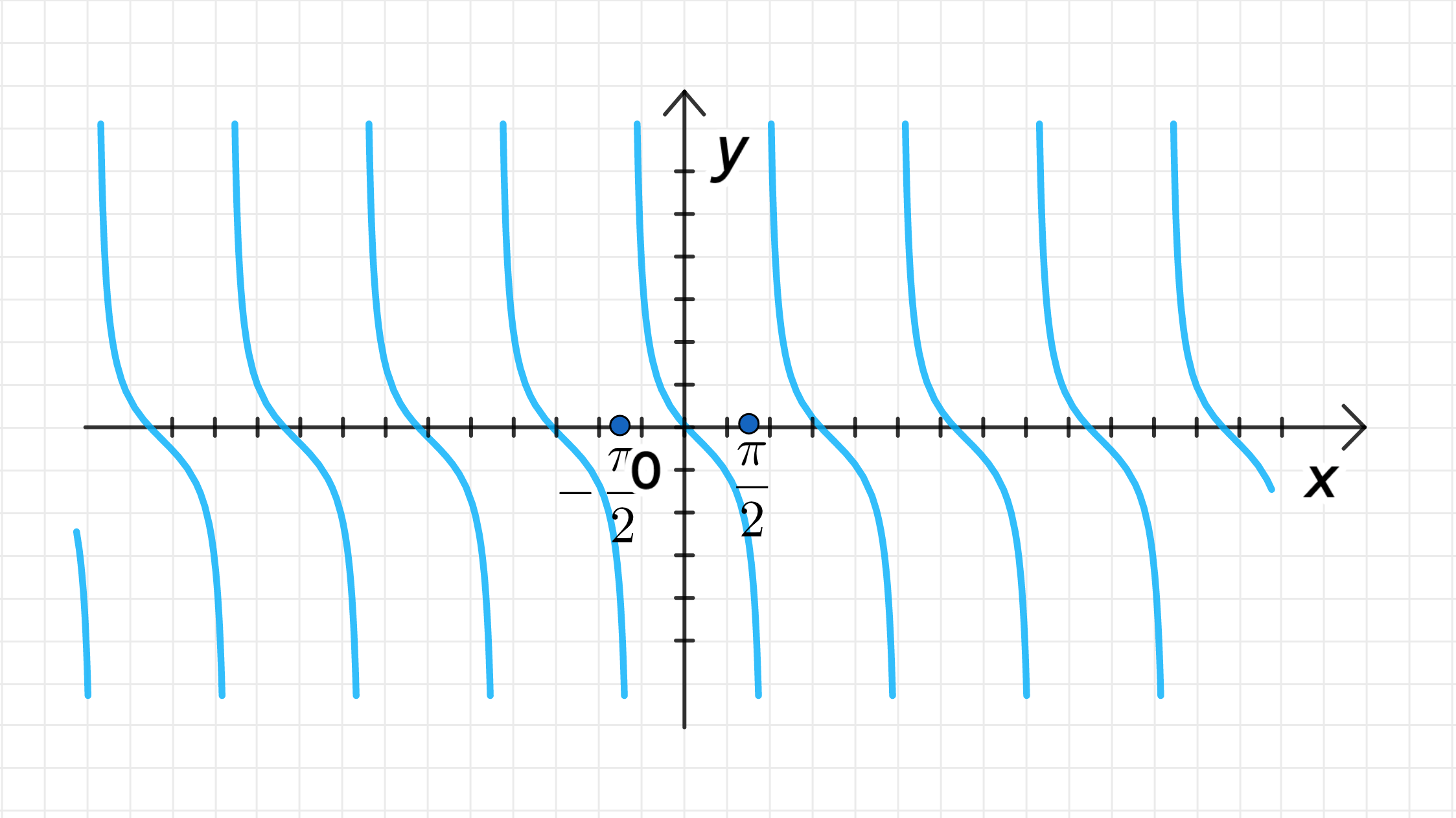
Постройте график функции:

а) $y = \operatorname{ctg} \left( x + \frac{\pi}{2} \right)$;

б) $y = \operatorname{ctg} \, x + 1$;

в) $y = \operatorname{ctg} \left( x — \frac{\pi}{3} \right)$;

г) $y=\mathrm{ctg}x-2$

а) $y = \operatorname{ctg} \left( x + \frac{\pi}{2} \right)$;

Главная ветвь тангенсоиды имеет центр в точке:

$$x_0 = \frac{\pi}{2} — \frac{\pi}{2} = 0 \quad \text{и} \quad y_0 = 0;$$

Ветвь лежит на интервале:

$$0 — \frac{\pi}{2} < x < \pi — \frac{\pi}{2};$$ $$-\frac{\pi}{2} < x < \frac{\pi}{2};$$

График функции:

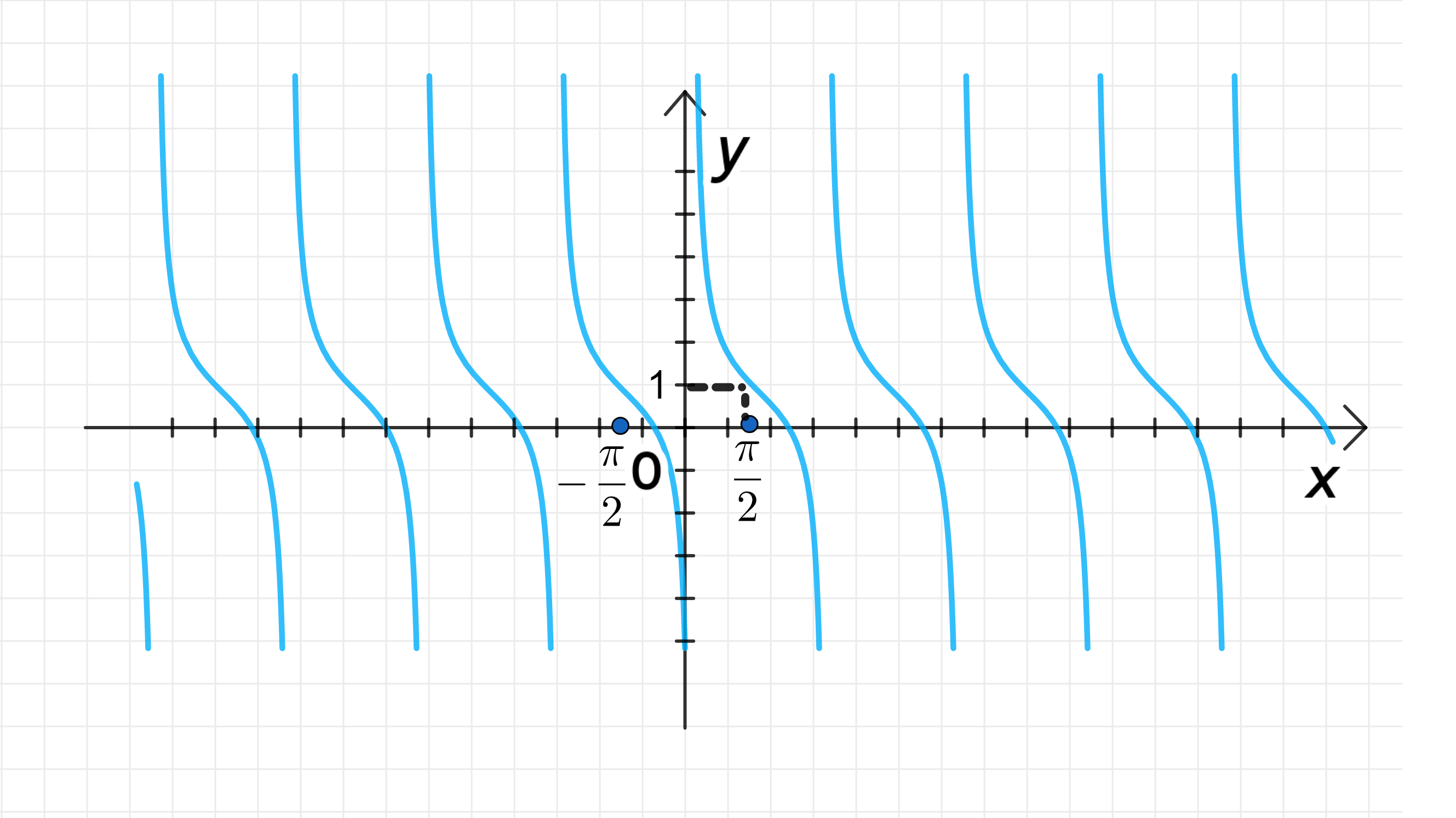
б) $y = \operatorname{ctg} \, x + 1$;

Главная ветвь тангенсоиды имеет центр в точке:

$$x_0 = \frac{\pi}{2} \quad \text{и} \quad y_0 = 0 + 1 = 1;$$

Ветвь лежит на интервале: $0 < x < \pi$;

График функции:

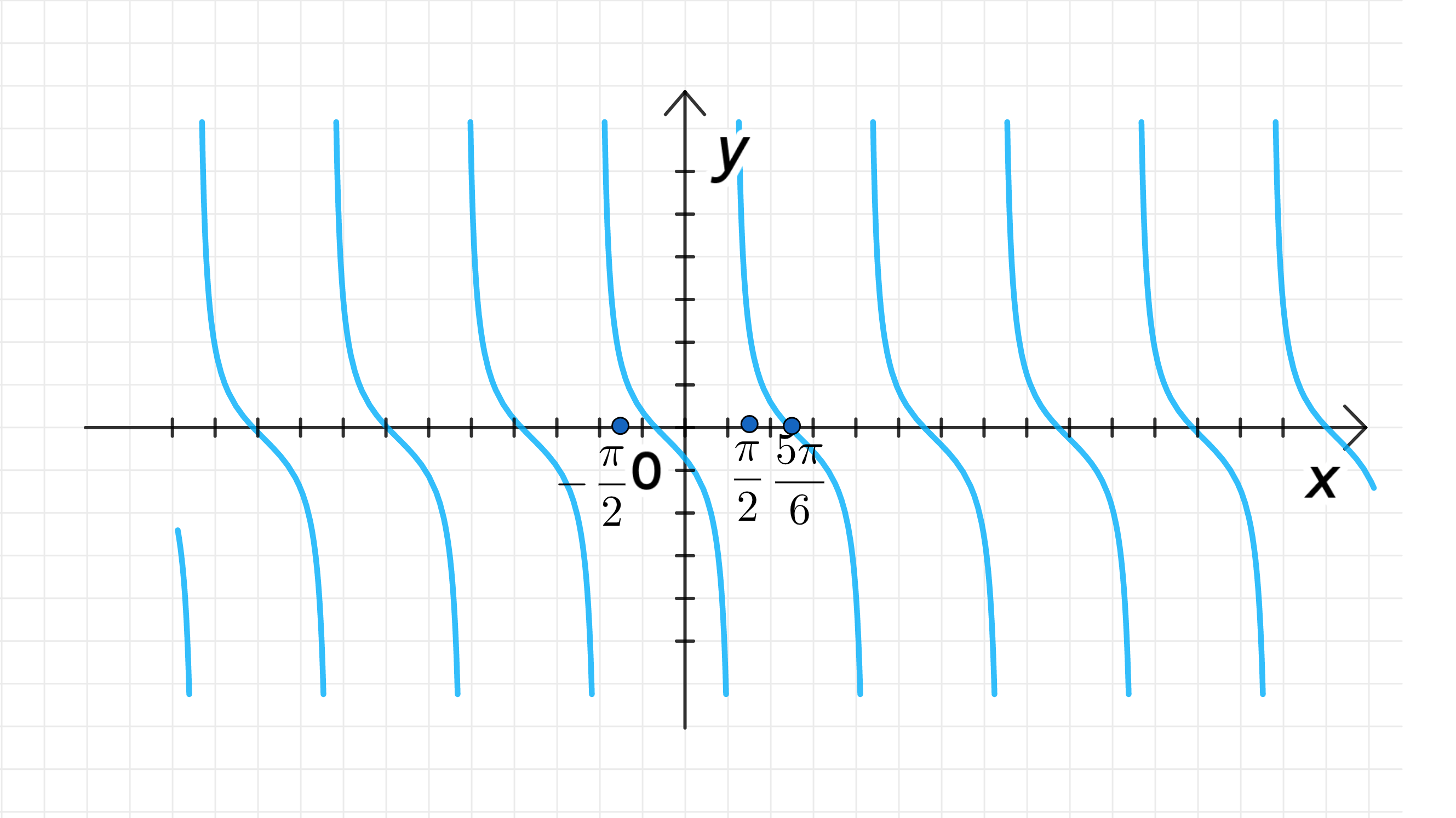
в) $y = \operatorname{ctg} \left( x — \frac{\pi}{3} \right)$;

Главная ветвь тангенсоиды имеет центр в точке:

$$x_0 = \frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6} \quad \text{и} \quad y_0 = 0;$$

Ветвь лежит на интервале:

$$0 + \frac{\pi}{3} < x < \pi + \frac{\pi}{3};$$ $$\frac{\pi}{3} < x < \frac{4\pi}{3};$$

График функции:

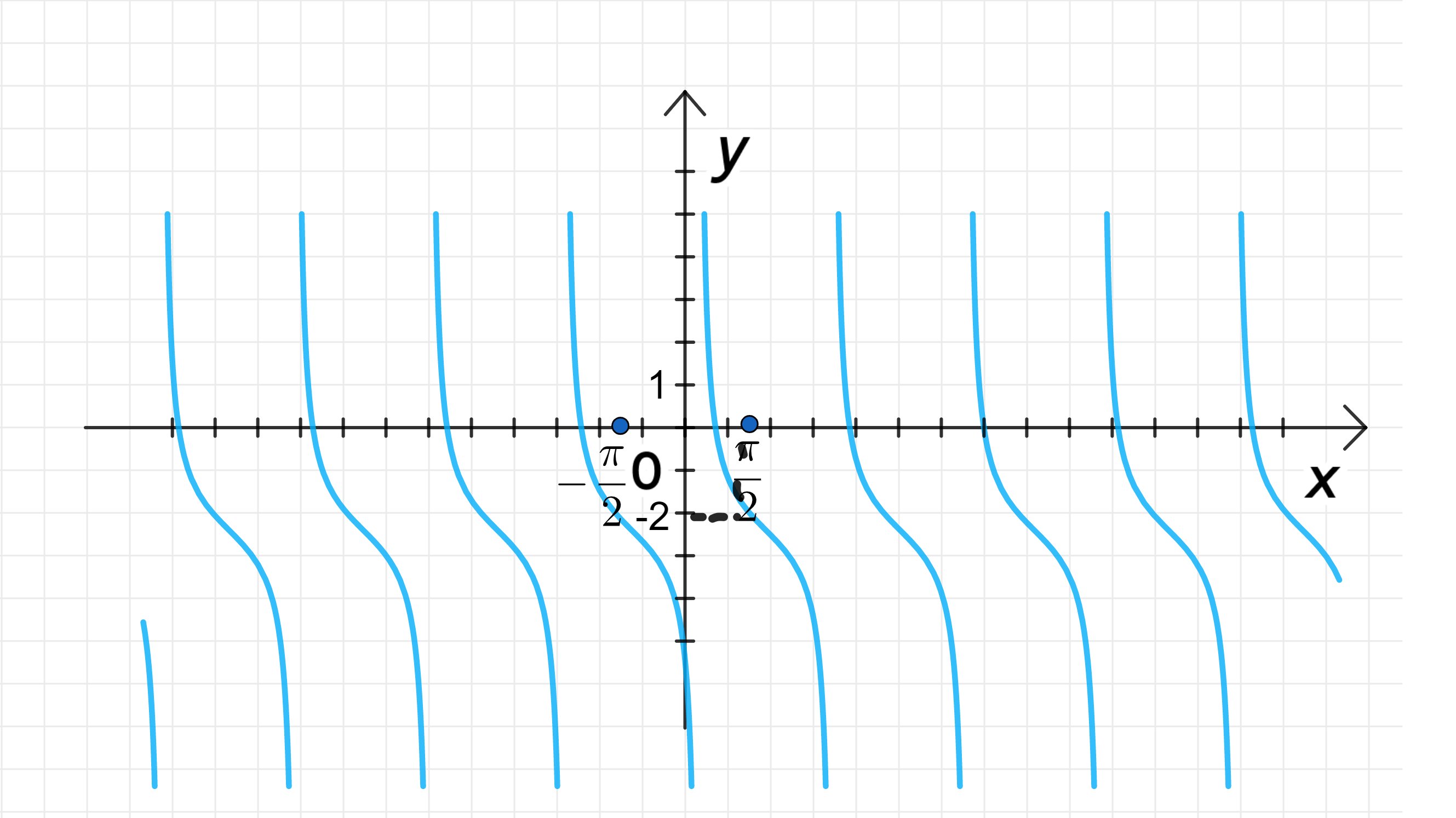
г) $y = \operatorname{ctg} \, x — 2$;

Главная ветвь тангенсоиды имеет центр в точке:

$$x_0 = \frac{\pi}{2} \quad \text{и} \quad y_0 = 0 — 2 = -2;$$

Ветвь лежит на интервале: $0 < x < \pi$;

График функции:

а) $y = \operatorname{ctg} \left( x + \frac{\pi}{2} \right)$

1) Главная ветвь тангенсоиды

Главная ветвь тангенсоиды функции $\operatorname{ctg}(x)$ обычно имеет центр в точке $x_0 = \frac{\pi}{2}$, где функция изменяет свои знаки и периодически повторяется. Но в этом случае в аргументе функции присутствует сдвиг на $\frac{\pi}{2}$ вправо, то есть мы должны учесть этот сдвиг.

Применим сдвиг $+\frac{\pi}{2}$ к обычной функции $\operatorname{ctg}(x)$. Сдвиг на $\frac{\pi}{2}$ вправо сдвигает центр главной ветви функции на $x_0 = 0$.

Результат:

$$x_0 = \frac{\pi}{2} — \frac{\pi}{2} = 0 \quad \text{и} \quad y_0 = 0.$$

2) Интервал для функции

При обычной функции $\operatorname{ctg}(x)$ главная ветвь лежит на интервале $0 < x < \pi$, так как период функции составляет $\pi$. Из-за сдвига на $\frac{\pi}{2}$ вправо, интервал изменяется следующим образом:

• Начало интервала $0 — \frac{\pi}{2} = -\frac{\pi}{2}$,
• Конец интервала $\pi — \frac{\pi}{2} = \frac{\pi}{2}$.

Результат:

$$-\frac{\pi}{2} < x < \frac{\pi}{2}.$$

3) График функции

б) $y = \operatorname{ctg} \, x + 1$

1) Главная ветвь тангенсоиды

Теперь у нас есть функция $y = \operatorname{ctg} \, x + 1$, которая представляет собой график стандартной функции $\operatorname{ctg}(x)$, сдвинутый по вертикали на 1 единицу вверх.

Это значит, что центр главной ветви функции будет находиться в точке $x_0 = \frac{\pi}{2}$, и $y_0 = 0 + 1 = 1$.

Результат:

$$x_0 = \frac{\pi}{2} \quad \text{и} \quad y_0 = 1.$$

2) Интервал для функции

График функции будет располагаться на интервале $0 < x < \pi$, так как это стандартный период функции $\operatorname{ctg}(x)$, и вертикальный сдвиг на 1 единицу вверх не изменяет интервал.

Результат:

$$0 < x < \pi.$$

3) График функции

в) $y = \operatorname{ctg} \left( x — \frac{\pi}{3} \right)$

1) Главная ветвь тангенсоиды

Здесь у нас имеется сдвиг функции $\operatorname{ctg}(x)$ на $\frac{\pi}{3}$ вправо. Это значит, что центр главной ветви функции сдвигается на $\frac{\pi}{3}$ вправо от стандартного положения $x_0 = \frac{\pi}{2}$.

Таким образом, новый центр главной ветви будет в точке:

$$x_0 = \frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6} \quad \text{и} \quad y_0 = 0.$$

Результат:

$$x_0 = \frac{5\pi}{6} \quad \text{и} \quad y_0 = 0.$$

2) Интервал для функции

Теперь рассмотрим, как изменится интервал на основе сдвига. Стандартная функция $\operatorname{ctg}(x)$ имеет период $\pi$, и при сдвиге на $\frac{\pi}{3}$ вправо, интервалы также сдвигаются на этот сдвиг:

• Начало интервала будет сдвинуто на $\frac{\pi}{3}$ вправо, так что интервал будет от $\frac{\pi}{3}$ до $\frac{4\pi}{3}$.

Результат:

$$\frac{\pi}{3} < x < \frac{4\pi}{3}.$$

3) График функции

г) $y = \operatorname{ctg} \, x — 2$

1) Главная ветвь тангенсоиды

Здесь у нас сдвиг функции $\operatorname{ctg}(x)$ на $-2$ по оси $y$, то есть на 2 единицы вниз. Это значит, что центр главной ветви будет в точке:

$$x_0 = \frac{\pi}{2} \quad \text{и} \quad y_0 = 0 — 2 = -2.$$

Результат:

$$x_0 = \frac{\pi}{2} \quad \text{и} \quad y_0 = -2.$$

2) Интервал для функции

Как и в предыдущих примерах, интервал для функции остаётся таким же, поскольку вертикальный сдвиг не изменяет период функции. Интервал будет $0 < x < \pi$.

Результат:

$$0 < x < \pi.$$

3) График функции