Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 20.19 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а) ;
б) ;
в) ;
г)
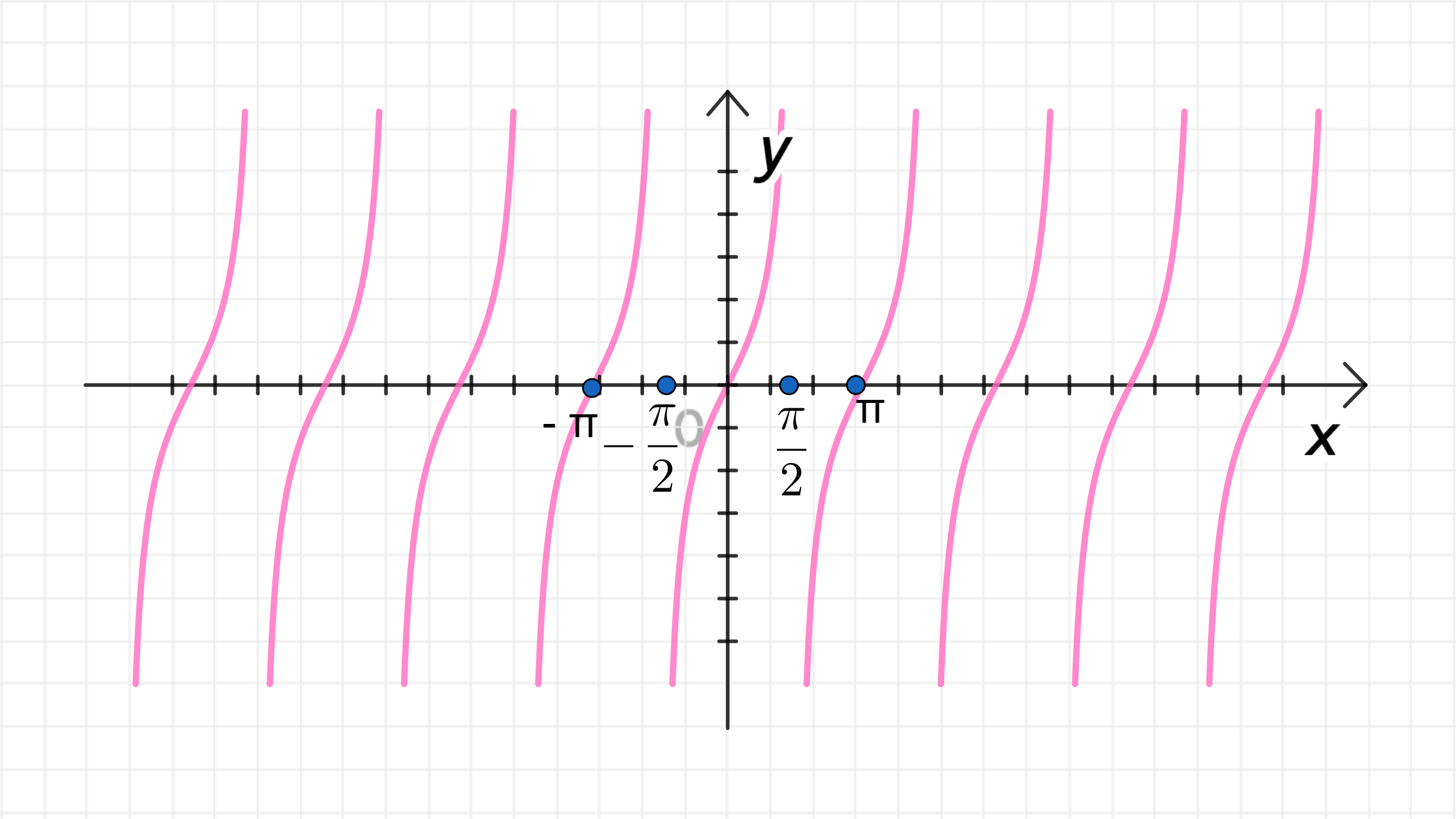
а) ;
Построим главную ветвь функции ;
Растянем ее от оси с коэффициентом ;
Достроим график функции:
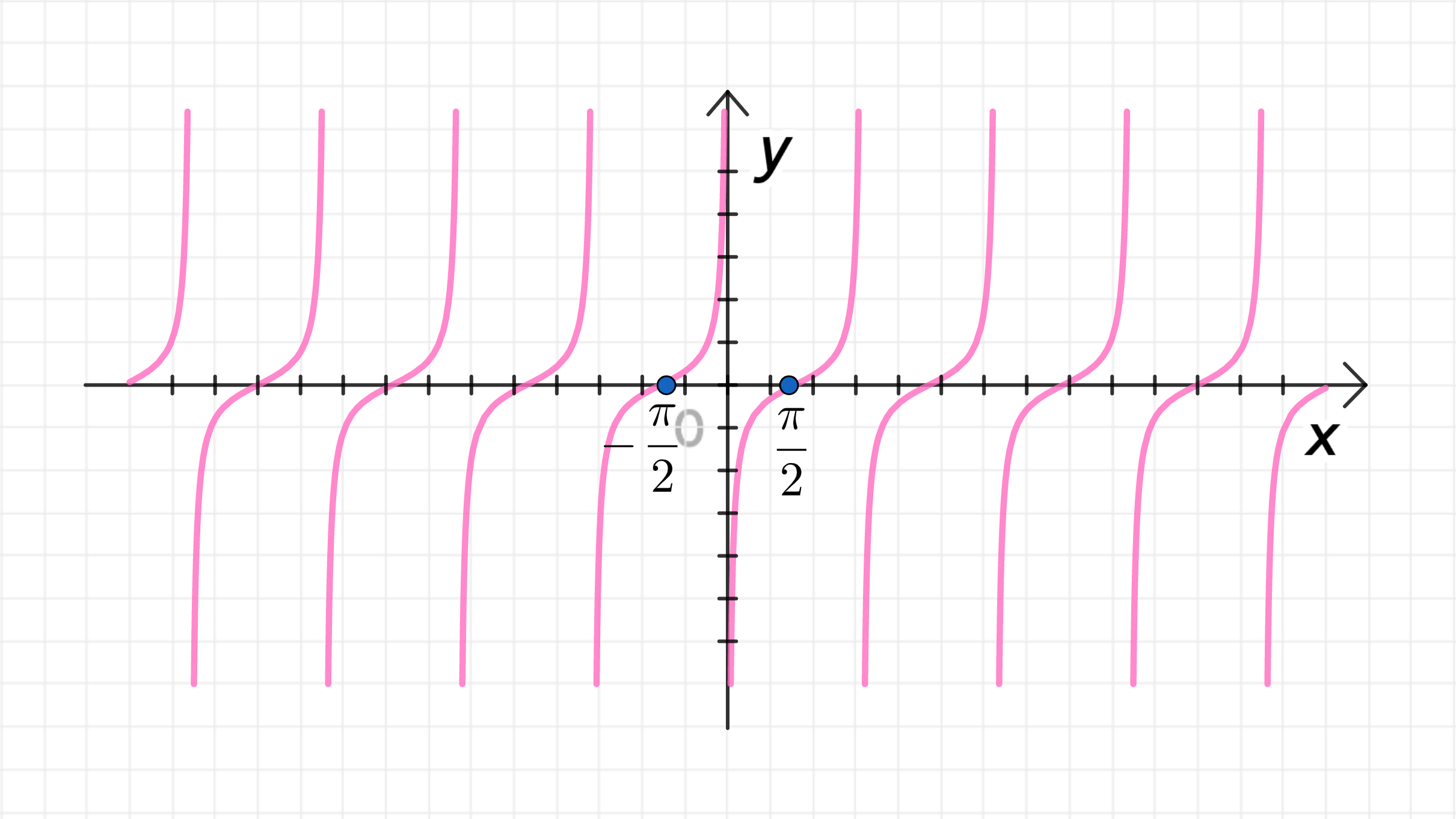
б) ;
Построим главную ветвь функции ;
Сожмем ее к оси с коэффициентом ;
Достроим график функции:
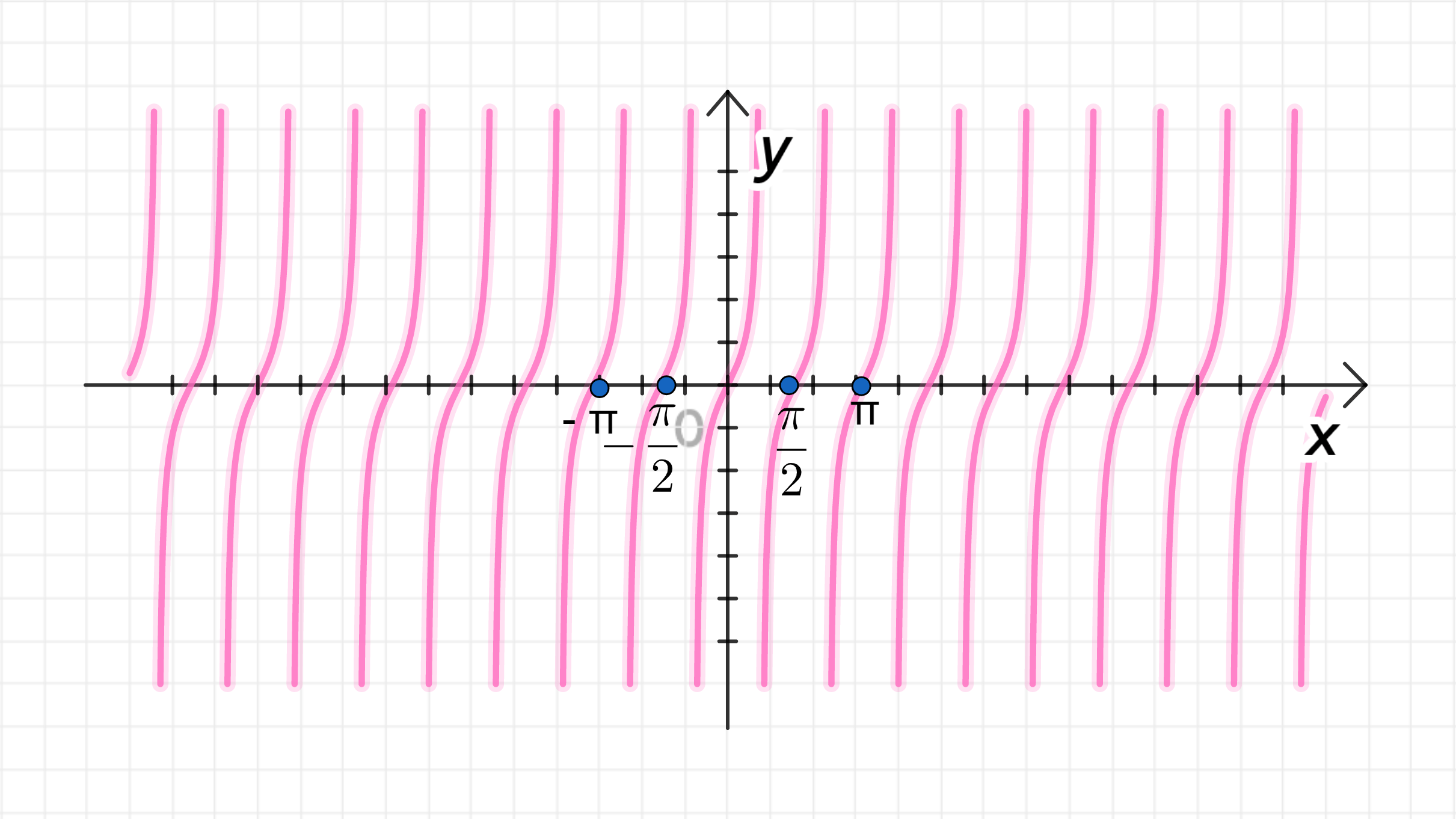
в) ;
Построим главную ветвь функции ;
Сожмем ее к оси с коэффициентом ;
Основной период функции:
Достроим график функции:
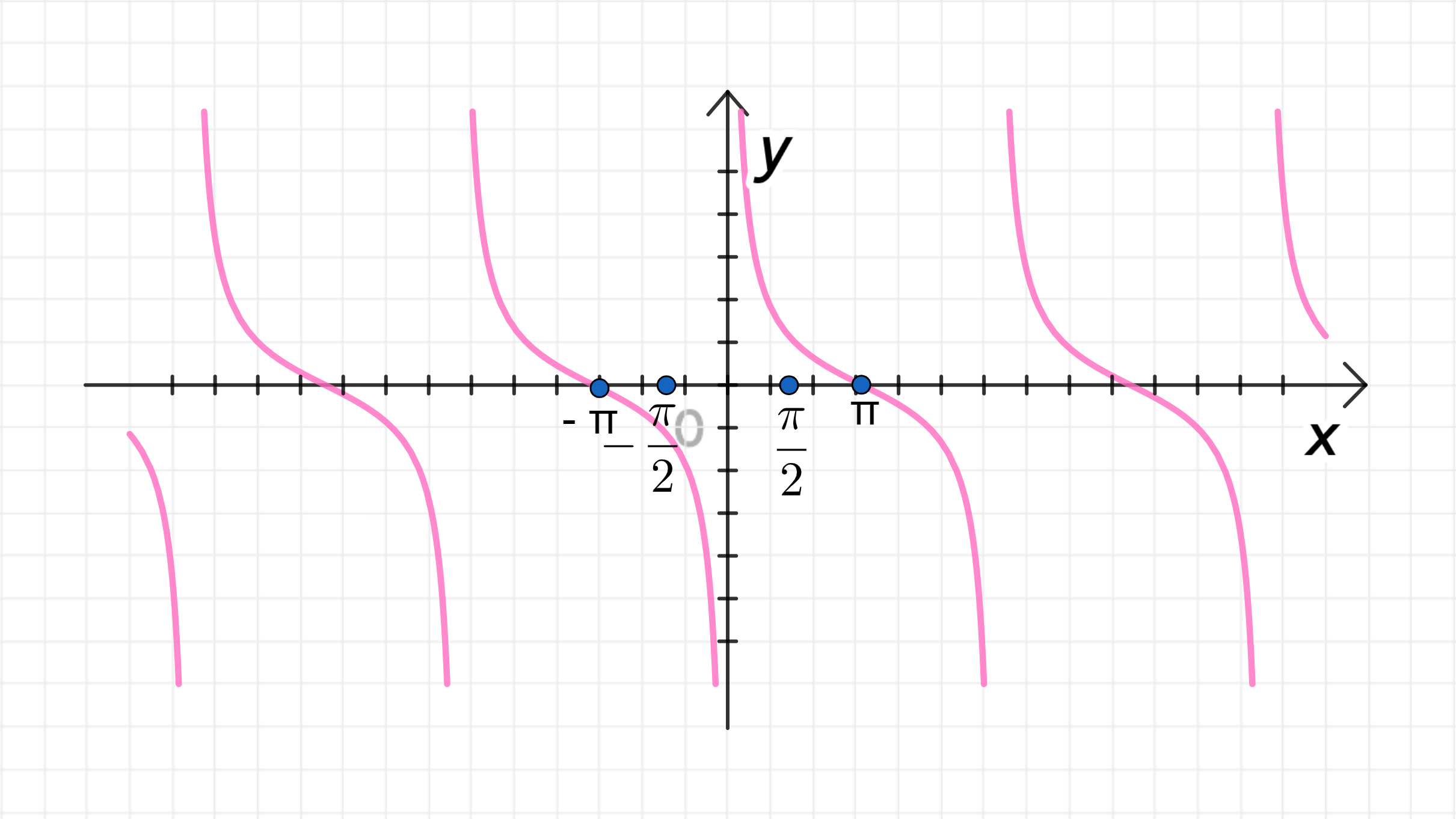
г) ;
Построим главную ветвь функции ;
Растянем ее от оси с коэффициентом ;
Основной период функции:
Достроим график функции:
а)
1) Построение главной ветви функции
График функции — это стандартная тангенсоида. Эта функция имеет следующие ключевые свойства:
- Асимптоты в точках , где .
- Период .
- Центр (точка пересечения с осью ) в точке , где .
2) Растяжение функции от оси с коэффициентом
Когда мы умножаем функцию на коэффициент , это вызывает растяжение графика функции по оси . То есть, значения функции на каждой точке увеличиваются в два раза, а сама функция становится «выше», но сохраняет свои асимптоты и период.
Математически это выражается как:
Если , то . Это увеличение амплитуды функции.
3) Достроим график функции
б)
1) Построение главной ветви функции
График функции имеет следующие особенности:
- Асимптоты в точках , где .
- Период функции .
- График начинает падение с при и стремится к при .
Когда перед функцией появляется минус, то график переворачивается. Это значит, что функция будет стремиться к в точке и к в точке , но с противоположным направлением. То есть, функция меняет свой «наклон».
2) Сжатие функции к оси с коэффициентом
Когда мы умножаем функцию на коэффициент , это приводит к сжатию графика функции по оси . Коэффициент фактически означает, что вертикальная амплитуда функции уменьшится в два раза, а график будет сжат по вертикали, но асимптоты останутся на тех же местах.
Математически это можно выразить как:
3) Достроим график функции
в)
1) Построение главной ветви функции
Как и в предыдущих примерах, функция — это стандартная тангенсоида. Она имеет:
- Период ,
- Асимптоты в точках , где ,
- Центр в точке , где .
2) Сжатие функции к оси с коэффициентом
Умножение аргумента функции на изменяет период функции. Если обычная функция имеет период , то функция будет иметь период:
Таким образом, функция будет «сжата» по оси , и график будет повторяться дважды быстрее.
3) Основной период функции
Для функции период изменяется следующим образом:
То есть период сокращается в два раза, и функция будет повторяться за .
4) Достроим график функции
г)
1) Построение главной ветви функции
Как и раньше, функция имеет:
- Период ,
- Асимптоты в точках , где ,
- Центр в точке .
2) Растяжение функции от оси с коэффициентом
Когда аргумент функции делится на 2, это приводит к растяжению графика по оси . То есть, функция будет «растянута» по оси , и её период увеличится в два раза. В этом случае период функции станет .
Математически это можно записать как:
3) Основной период функции
Для функции период изменяется следующим образом:
Таким образом, период функции увеличился в два раза, и теперь функция будет повторяться на интервале .
4) Достроим график функции