ГДЗ по Алгебре 10 Класс Номер 20.2 Профильный Уровень Мордкович — Подробные Ответы

Решите графически уравнение:

а) $\mathrm{tg}x=-\sqrt{3}$

б) $\mathrm{tg}x=1$

в) $\mathrm{tg}x=-1$

г) $\mathrm{tg}x=0$

а) $\operatorname{tg} x = -\sqrt{3}$

Построим графики функций $y = \operatorname{tg} x$ и $y = -\sqrt{3} \approx -1,75$;

Графики пересекаются в точке: $x = -\frac{\pi}{3}$;

Расстояние между соседними точками пересечения равно $\pi$;

Ответ: $x = -\frac{\pi}{3} + \pi n$.

б) $\operatorname{tg} x = 1$

Построим графики функций $y = \operatorname{tg} x$ и $y = 1$;

Графики пересекаются в точке: $x = \frac{\pi}{4}$;

Расстояние между соседними точками пересечения равно $\pi$;

Ответ: $x = \frac{\pi}{4} + \pi n$.

в) $\operatorname{tg} x = -1$

Построим графики функций $y = \operatorname{tg} x$ и $y = -1$;

Графики пересекаются в точке: $x = -\frac{\pi}{4}$;

Расстояние между соседними точками пересечения равно $\pi$;

Ответ: $x = -\frac{\pi}{4} + \pi n$.

г) $\operatorname{tg} x = 0$

Построим график функции $y = \operatorname{tg} x$;

График пересекает ось абсцисс в точке: $x = 0$;

Расстояние между соседними точками пересечения равно $\pi$;

Ответ: $x = \pi n$.

а) $\operatorname{tg} x = -\sqrt{3}$

Построение графиков функций:

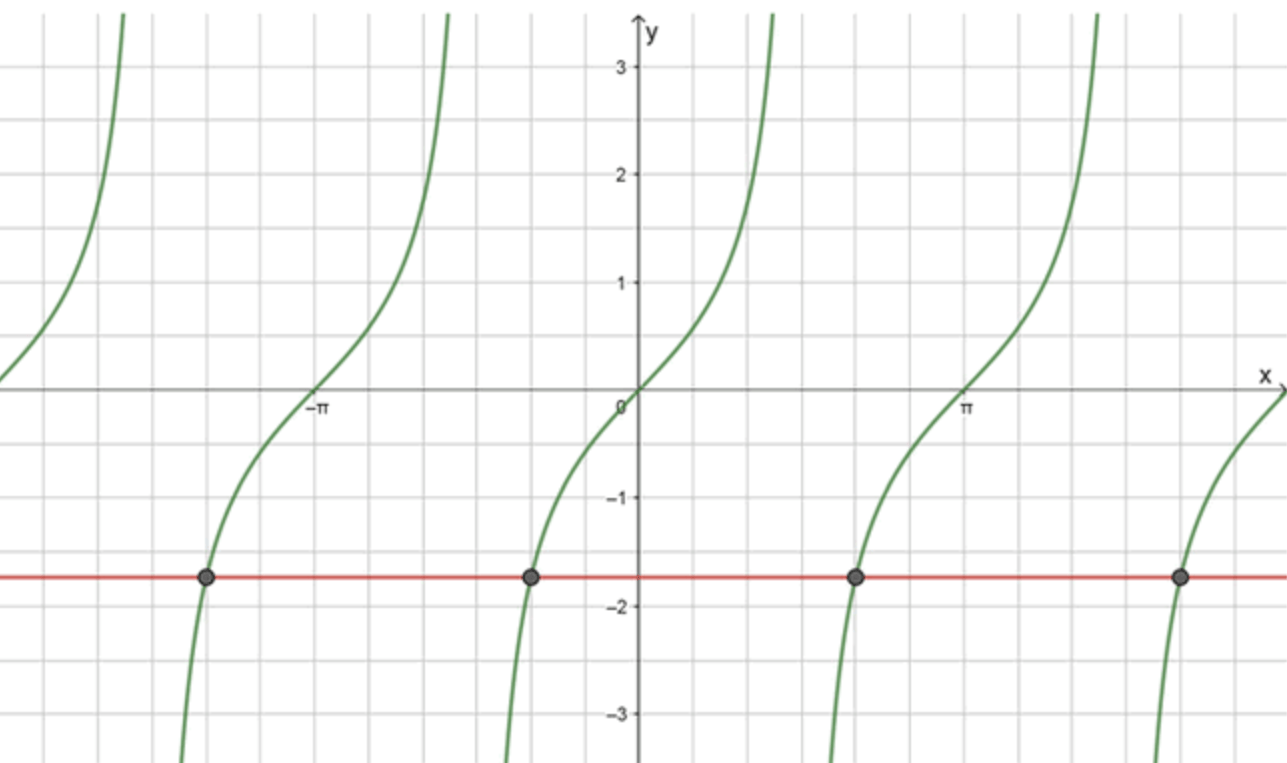
Для того чтобы построить график функции $y = \operatorname{tg} x$, мы знаем, что тангенс имеет период $\pi$ и вертикальные асимптоты при $x = \frac{\pi}{2} + n\pi$, где $n$ — целое число. Кроме того, функция $y = \operatorname{tg} x$ проходит через точку $(0, 0)$, а на интервале $-\frac{\pi}{2} < x < \frac{\pi}{2}$ график плавно переходит от минус бесконечности в точке $x = -\frac{\pi}{2}$ к бесконечности в точке $x = \frac{\pi}{2}$.

Теперь строим график функции $y = -\sqrt{3}$. Это прямая, параллельная оси абсцисс, с постоянным значением $y = -\sqrt{3} \approx -1,75$.

Пересечение графиков:

Для нахождения точек пересечения графиков функции $y = \operatorname{tg} x$ и прямой $y = -\sqrt{3}$, решим уравнение:

$$\operatorname{tg} x = -\sqrt{3}$$

Тангенс принимает значение $-\sqrt{3}$ в точке $x = -\frac{\pi}{3}$ в интервале $-\frac{\pi}{2} < x < \frac{\pi}{2}$, потому что:

$$\operatorname{tg} \left( -\frac{\pi}{3} \right) = -\sqrt{3}.$$

Таким образом, графики пересекаются в точке $x = -\frac{\pi}{3}$.

Расстояние между соседними точками пересечения:

Тангенс — периодическая функция с периодом $\pi$. Это означает, что если одна точка пересечения находится в точке $x = -\frac{\pi}{3}$, то следующая точка пересечения будет через $\pi$ единиц вправо, то есть в точке:

$$x = -\frac{\pi}{3} + \pi.$$

Таким образом, расстояние между соседними точками пересечения равно $\pi$.

Ответ: $x = -\frac{\pi}{3} + \pi n$, где $n$ — целое число.

б) $\operatorname{tg} x = 1$

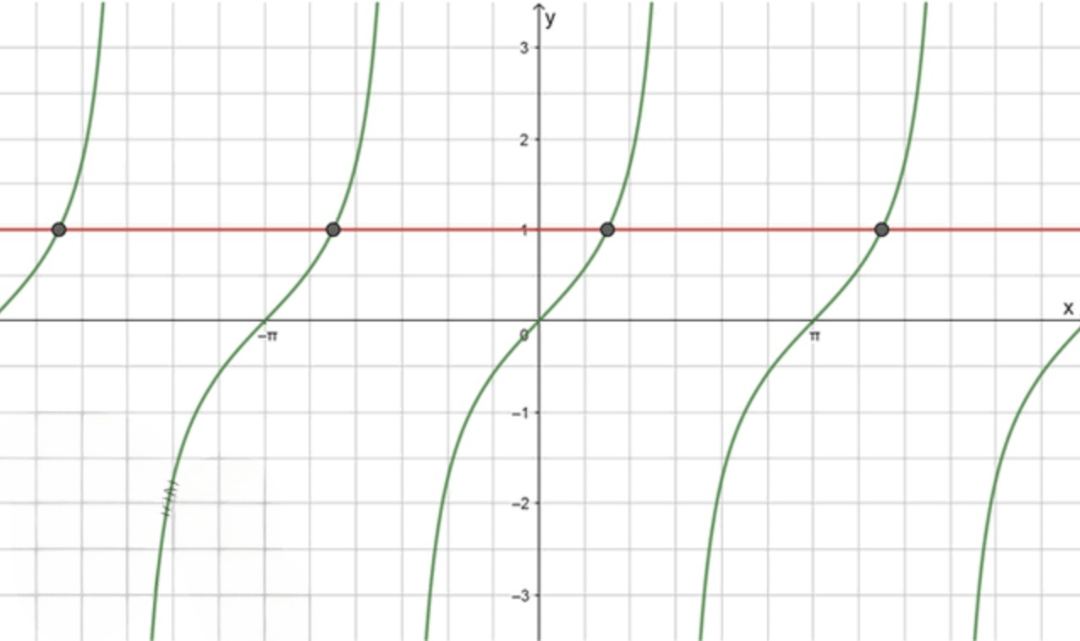
Построение графиков функций:

Мы строим график функции $y = \operatorname{tg} x$, который как и ранее имеет период $\pi$ и вертикальные асимптоты при $x = \frac{\pi}{2} + n\pi$.

Также строим прямую $y = 1$, которая горизонтальна и пересекает ось $y$ в точке 1.

Пересечение графиков:

Для нахождения точек пересечения решаем уравнение:

$$\operatorname{tg} x = 1.$$

Тангенс принимает значение 1 в точке $x = \frac{\pi}{4}$ на интервале $-\frac{\pi}{2} < x < \frac{\pi}{2}$, потому что:

$$\operatorname{tg} \left( \frac{\pi}{4} \right) = 1.$$

Таким образом, графики пересекаются в точке $x = \frac{\pi}{4}$.

Расстояние между соседними точками пересечения:

Как и в предыдущем случае, тангенс — периодическая функция с периодом $\pi$. Следовательно, следующая точка пересечения будет через $\pi$ единиц вправо, то есть в точке:

$$x = \frac{\pi}{4} + \pi.$$

Расстояние между соседними точками пересечения равно $\pi$.

Ответ: $x = \frac{\pi}{4} + \pi n$, где $n$ — целое число.

в) $\operatorname{tg} x = -1$

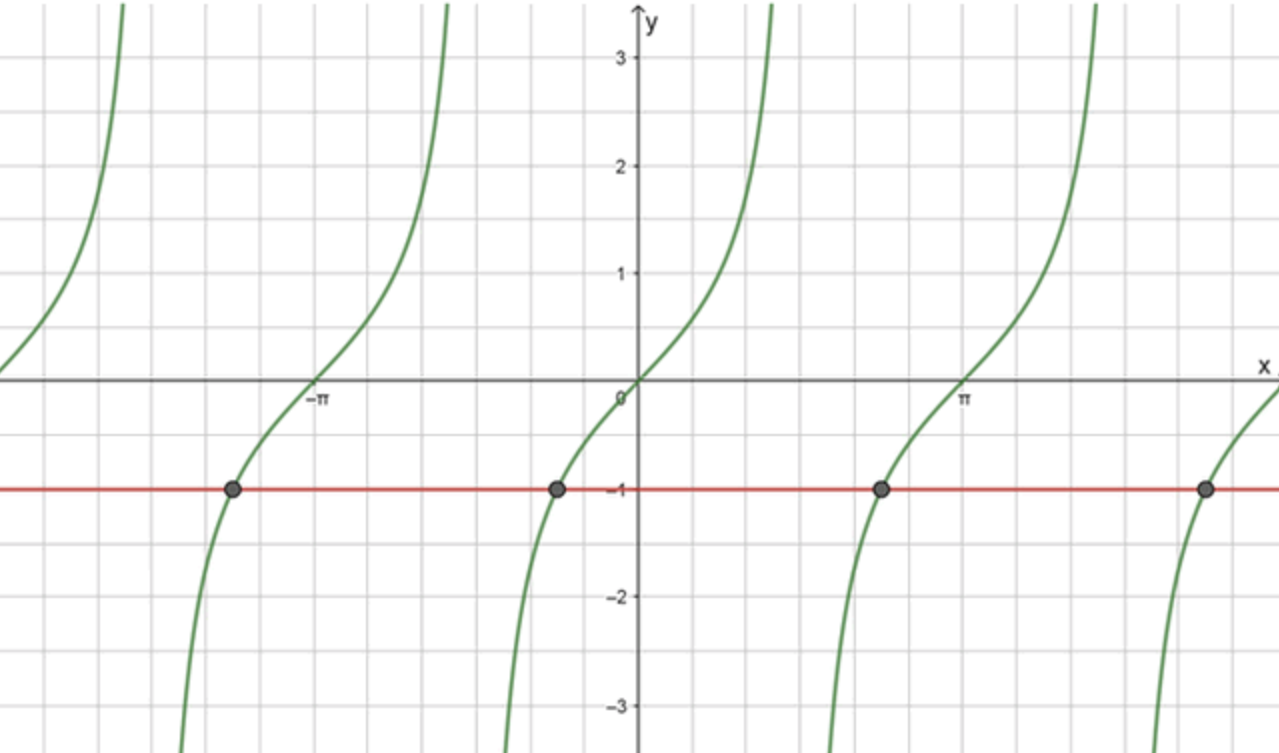
Построение графиков функций:

Строим график функции $y = \operatorname{tg} x$, который опять же имеет период $\pi$ и вертикальные асимптоты при $x = \frac{\pi}{2} + n\pi$.

Строим прямую $y = -1$, которая горизонтальна и пересекает ось $y$ в точке -1.

Пересечение графиков:

Для нахождения точек пересечения решаем уравнение:

$$\operatorname{tg} x = -1.$$

Тангенс принимает значение -1 в точке $x = -\frac{\pi}{4}$ на интервале $-\frac{\pi}{2} < x < \frac{\pi}{2}$, потому что:

$$\operatorname{tg} \left( -\frac{\pi}{4} \right) = -1.$$

Таким образом, графики пересекаются в точке $x = -\frac{\pi}{4}$.

Расстояние между соседними точками пересечения:

Так как тангенс имеет период $\pi$, следующая точка пересечения будет через $\pi$ единиц вправо, то есть в точке:

$$x = -\frac{\pi}{4} + \pi.$$

Расстояние между соседними точками пересечения равно $\pi$.

Ответ: $x = -\frac{\pi}{4} + \pi n$, где $n$ — целое число.

г) $\operatorname{tg} x = 0$

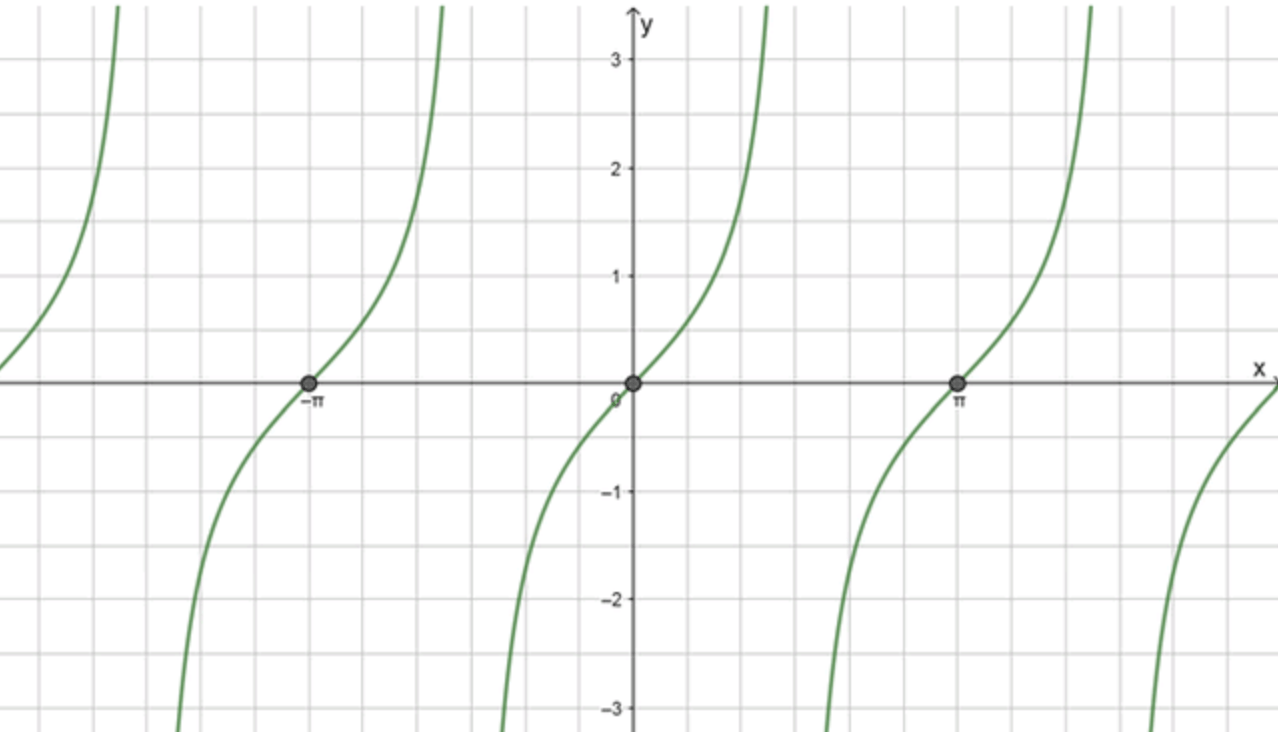
Построение графика функции:

График функции $y = \operatorname{tg} x$ пересекает ось абсцисс в точке $x = 0$ и имеет период $\pi$. График стремится к бесконечности при $x = \frac{\pi}{2} + n\pi$ и уходит в минус бесконечность при $x = -\frac{\pi}{2} + n\pi$.

Пересечение с осью абсцисс:

Для нахождения точек пересечения с осью абсцисс решаем уравнение:

$$\operatorname{tg} x = 0.$$

Тангенс равен нулю в точках $x = 0, \pm \pi, \pm 2\pi, \dots$, то есть в точках вида $x = \pi n$, где $n$ — целое число.

Расстояние между соседними точками пересечения:

Период функции $\operatorname{tg} x$ равен $\pi$, и она пересекает ось абсцисс в точках с шагом $\pi$, например: $x = 0, \pi, -\pi, 2\pi, -2\pi, \dots$.

Следовательно, расстояние между соседними точками пересечения равно $\pi$.

Ответ: $x = \pi n$, где $n$ — целое число.