ГДЗ по Алгебре 10 Класс Номер 20.21 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

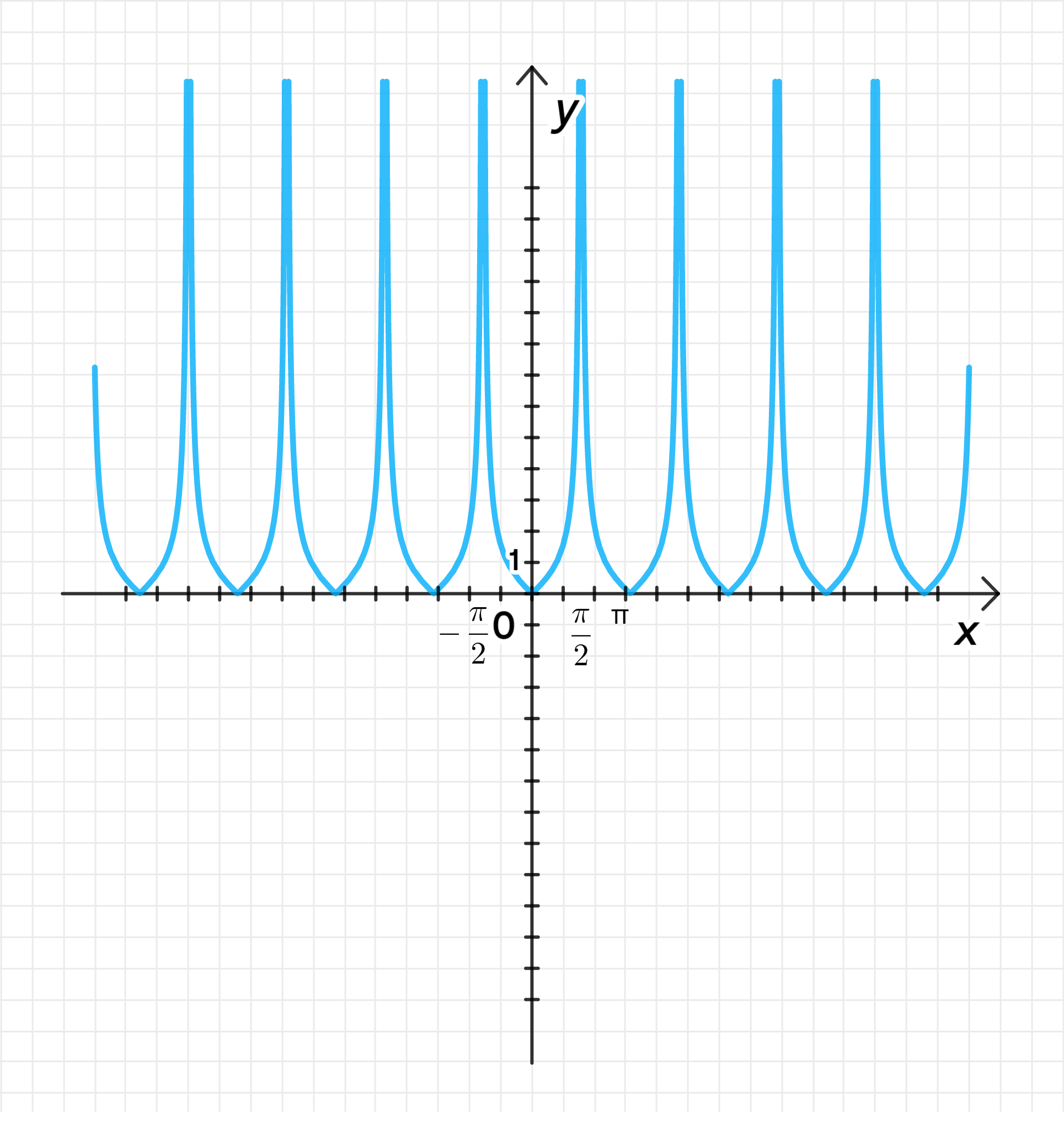
а) у = |tgх|;

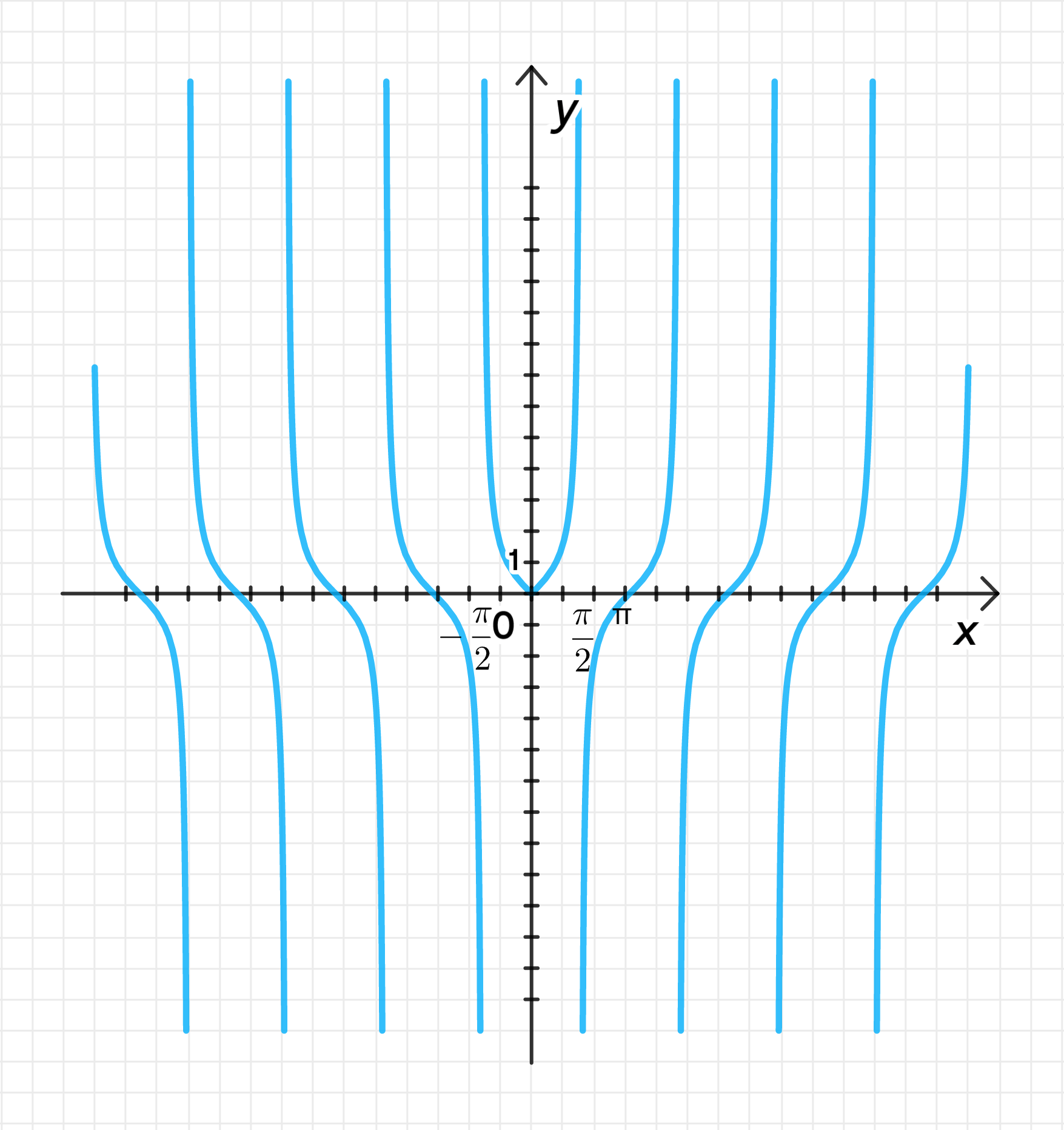
б) у = tg|x|;

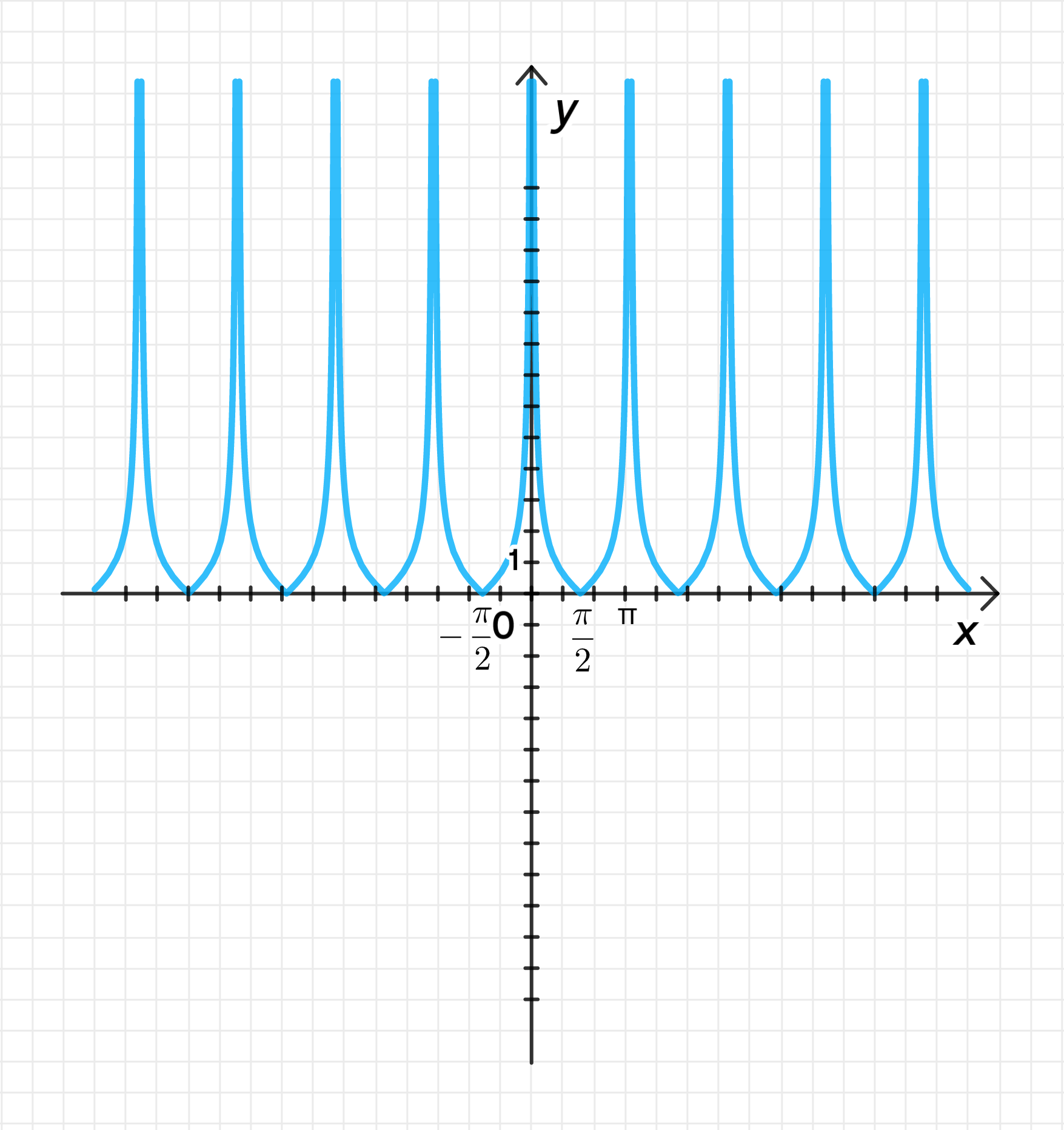
в) у = |ctgх|;

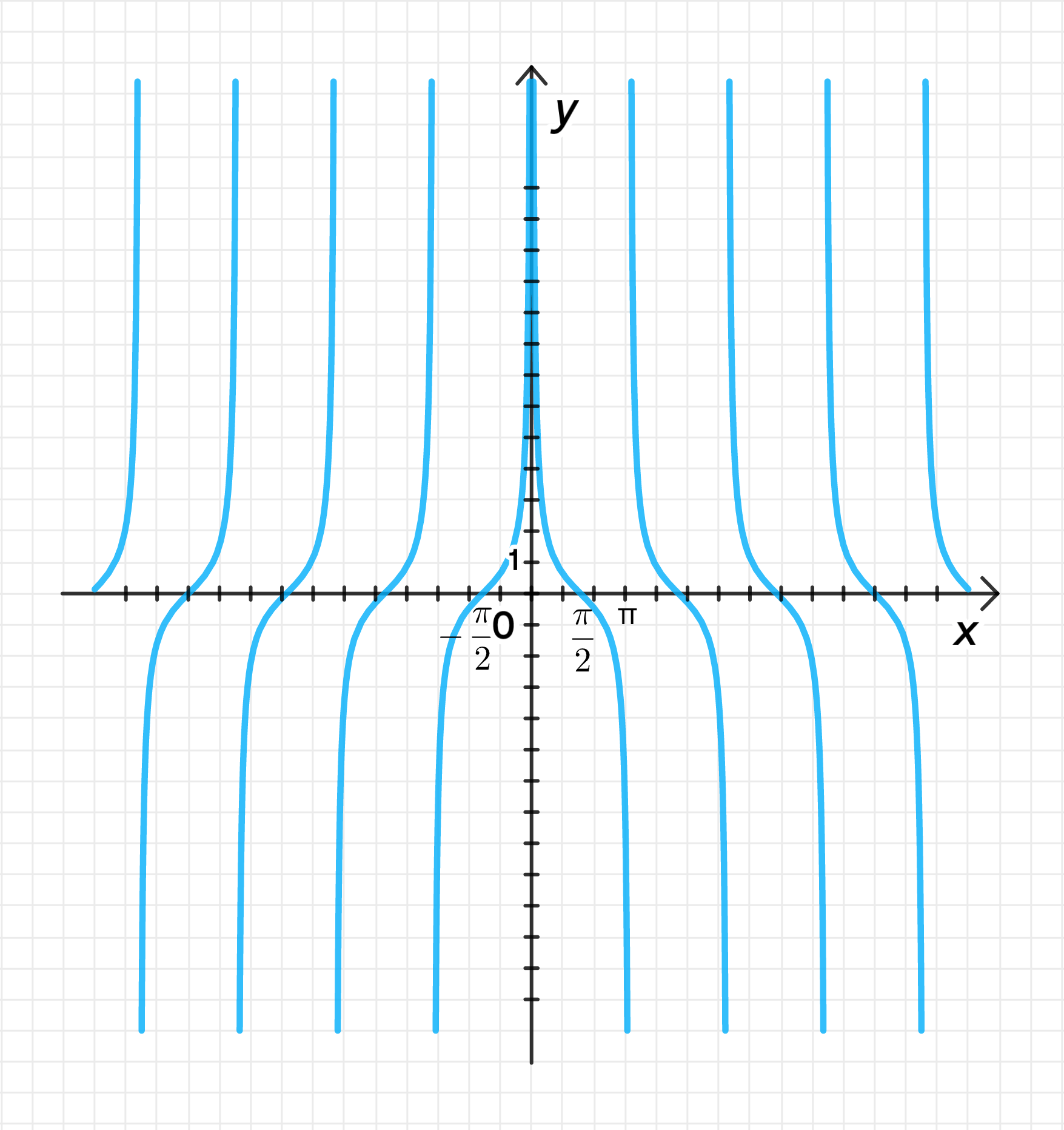
г) у = ctg|x|.

а) $y = |\operatorname{tg} x|$;

Если $\operatorname{tg} x \geq 0$, тогда:

$$y = \operatorname{tg} x;$$

Если $\operatorname{tg} x < 0$, тогда:

$$y = -\operatorname{tg} x;$$

График функции:

б) $y = \operatorname{tg} |x|$;

Если $x \geq 0$, тогда:

$$y = \operatorname{tg} x;$$

Если $x < 0$, тогда:

$$y = \operatorname{tg}(-x) = -\operatorname{tg} x;$$

График функции:

в) $y = |\operatorname{ctg} x|$;

Если $\operatorname{ctg} x \geq 0$, тогда:

$$y = \operatorname{ctg} x;$$

Если $\operatorname{ctg} x < 0$, тогда:

$$y = -\operatorname{ctg} x;$$

График функции:

г) $y = \operatorname{ctg} |x|$;

Если $x \geq 0$, тогда:

$$y = \operatorname{ctg} x;$$

Если $x < 0$, тогда:

$$y = \operatorname{ctg}(-x) = -\operatorname{ctg} x;$$

График функции:

а) $y = |\operatorname{tg} x|$

1) Если $\operatorname{tg} x \geq 0$, тогда:

Когда $\operatorname{tg} x \geq 0$, это означает, что тангенс положителен. В этом случае модуль функции $|\operatorname{tg} x|$ не изменяет значения функции, так как $|\operatorname{tg} x| = \operatorname{tg} x$ при $\operatorname{tg} x \geq 0$.

Таким образом, если $\operatorname{tg} x \geq 0$, то:

$$y = \operatorname{tg} x.$$

2) Если $\operatorname{tg} x < 0$, тогда:

Если $\operatorname{tg} x < 0$, это означает, что тангенс отрицателен. Модуль функции преобразует отрицательные значения в положительные, то есть:

$$y = -\operatorname{tg} x.$$

Это преобразование обеспечивает, что $y \geq 0$ для всех значений $x$, так как функция $|\operatorname{tg} x|$ всегда принимает неотрицательные значения.

3) График функции:

б) $y = \operatorname{tg} |x|$

1) Если $x \geq 0$, тогда:

Когда $x \geq 0$, мы имеем стандартную функцию $\operatorname{tg} x$, то есть:

$$y = \operatorname{tg} x.$$

График функции для $x \geq 0$ будет обычной тангенсоидой.

2) Если $x < 0$, тогда:

Когда $x < 0$, функция принимает вид $y = \operatorname{tg}(-x)$. Поскольку $\operatorname{tg}(-x) = -\operatorname{tg} x$, то:

$$y = -\operatorname{tg} x.$$

График будет симметричен графику для $x \geq 0$, но с обратным знаком, что приведет к отражению графика функции относительно оси $y = 0$.

3) График функции:

в) $y = |\operatorname{ctg} x|$

1) Если $\operatorname{ctg} x \geq 0$, тогда:

Если $\operatorname{ctg} x \geq 0$, то модуль функции не меняет ее значение, так как $|\operatorname{ctg} x| = \operatorname{ctg} x$ при $\operatorname{ctg} x \geq 0$.

Таким образом, если $\operatorname{ctg} x \geq 0$, то:

$$y = \operatorname{ctg} x.$$

2) Если $\operatorname{ctg} x < 0$, тогда:

Если $\operatorname{ctg} x < 0$, то модуль превращает отрицательные значения в положительные, то есть:

$$y = -\operatorname{ctg} x.$$

Таким образом, функция $|\operatorname{ctg} x|$ всегда будет неотрицательной.

3) График функции:

г) $y = \operatorname{ctg} |x|$

1) Если $x \geq 0$, тогда:

Когда $x \geq 0$, функция $y = \operatorname{ctg} x$ остается неизменной:

$$y = \operatorname{ctg} x.$$

График для $x \geq 0$ будет обычной котангенсоидой.

2) Если $x < 0$, тогда:

Когда $x < 0$, функция принимает вид $y = \operatorname{ctg}(-x)$. Поскольку $\operatorname{ctg}(-x) = -\operatorname{ctg} x$, то:

$$y = -\operatorname{ctg} x.$$

График будет зеркально отражен относительно оси $x$, что означает инверсию знаков функции на интервале $x < 0$.

3) График функции: