ГДЗ по Алгебре 10 Класс Номер 20.22 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) у = tgx + |tgх|;

б) у = |ctgx| — ctgx.

а) $y = \operatorname{tg} x + |\operatorname{tg} x|$;

Если $\operatorname{tg} x \geq 0$, тогда:

$$y = \operatorname{tg} x + \operatorname{tg} x = 2 \operatorname{tg} x;$$

Если $\operatorname{tg} x < 0$, тогда:

$$y = \operatorname{tg} x — \operatorname{tg} x = 0;$$

Область определения:

$$x \neq \frac{\pi}{2} + \pi n;$$

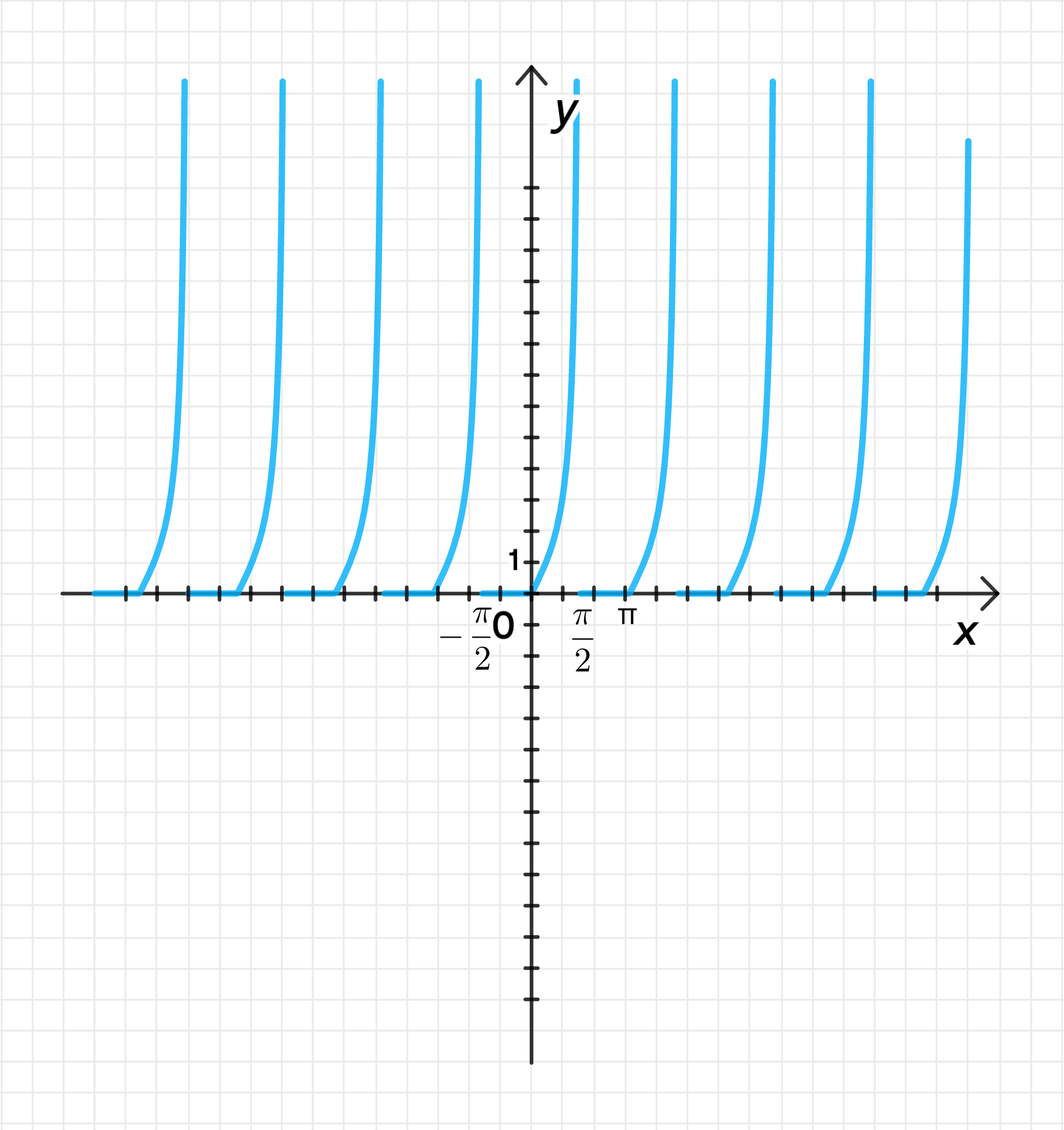
График функции:

б) $y = |\operatorname{ctg} x| — \operatorname{ctg} x$;

Если $\operatorname{ctg} x \geq 0$, тогда:

$$y = \operatorname{ctg} x — \operatorname{ctg} x = 0;$$

Если $\operatorname{tg} x < 0$, тогда:

$$y = -\operatorname{ctg} x — \operatorname{ctg} x = -2 \operatorname{ctg} x;$$

Область определения:

$$x \neq \pi n;$$

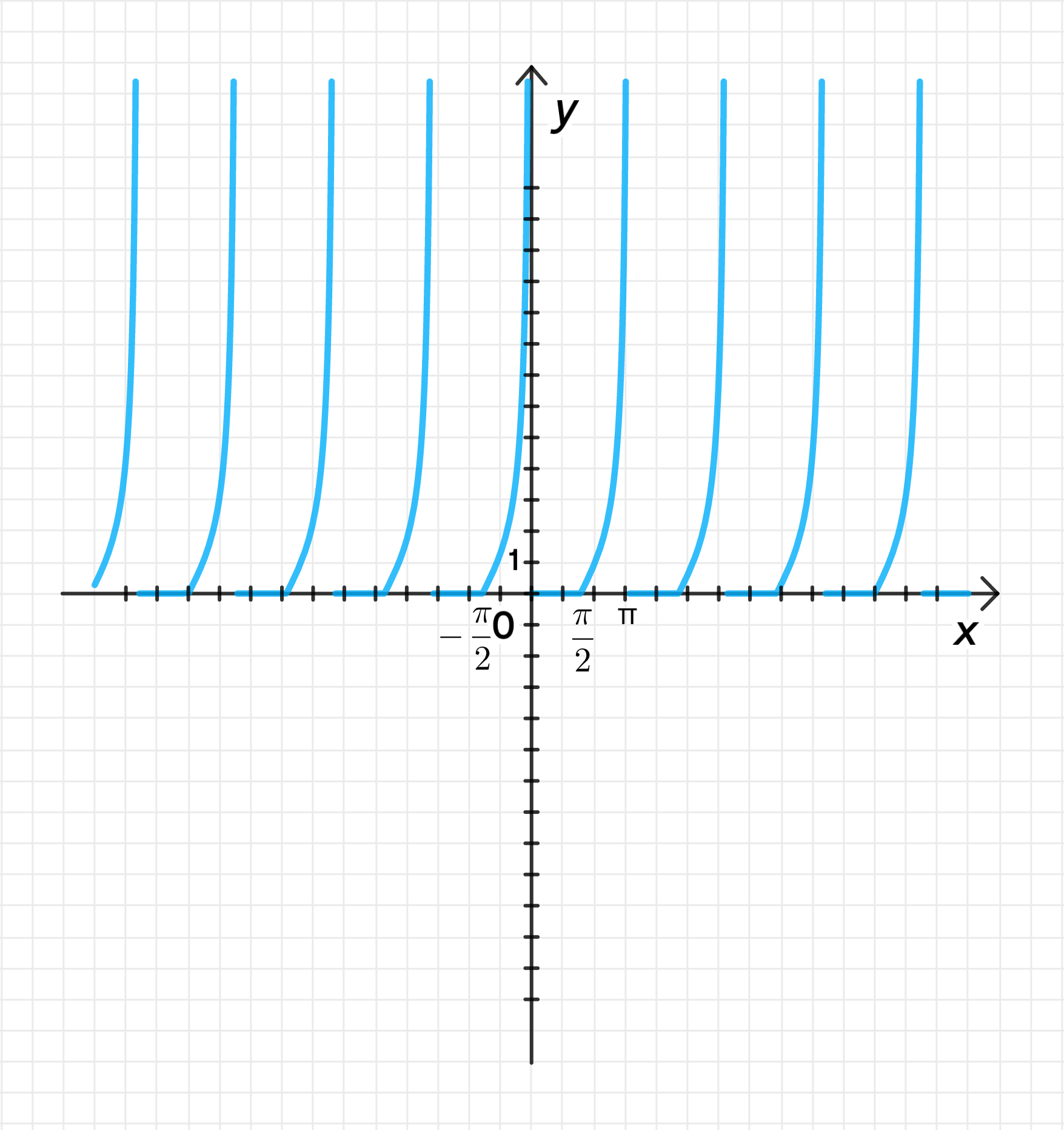
График функции:

а) $y = \operatorname{tg} x + |\operatorname{tg} x|$

1) Когда $\operatorname{tg} x \geq 0$:

• Если $\operatorname{tg} x \geq 0$, то $|\operatorname{tg} x| = \operatorname{tg} x$, так как модуль не изменяет положительные значения.
• Таким образом, в этом случае:

  $$y = \operatorname{tg} x + \operatorname{tg} x = 2 \operatorname{tg} x.$$

  Это означает, что функция удваивает значения тангенса, когда $\operatorname{tg} x$ положителен.

2) Когда $\operatorname{tg} x < 0$:

• Если $\operatorname{tg} x < 0$, то $|\operatorname{tg} x| = -\operatorname{tg} x$, так как модуль преобразует отрицательные значения в положительные.
• Таким образом, в этом случае:

  $$y = \operatorname{tg} x + (-\operatorname{tg} x) = 0.$$

  Это означает, что для отрицательных значений тангенса функция всегда принимает значение 0.

3) Область определения:

• Функция $y = \operatorname{tg} x$ имеет асимптоты в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
• Поскольку модуль не изменяет место разрыва функции, область определения не меняется.
• Таким образом, область определения функции:

  $$x \neq \frac{\pi}{2} + \pi n.$$

4) График функции:

• График функции будет следующим:
  • Для значений $\operatorname{tg} x \geq 0$ график будет удвоенным графиком стандартной тангенсоиды.
  • Для значений $\operatorname{tg} x < 0$ график будет представлять собой ось $y = 0$, так как $y = 0$ на этих промежутках.
  • График будет прерываться в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.

б) $y = |\operatorname{ctg} x| — \operatorname{ctg} x$

1) Когда $\operatorname{ctg} x \geq 0$:

• Если $\operatorname{ctg} x \geq 0$, то $|\operatorname{ctg} x| = \operatorname{ctg} x$, так как модуль не изменяет положительные значения.
• В этом случае:

  $$y = \operatorname{ctg} x — \operatorname{ctg} x = 0.$$

  Это означает, что на этих промежутках функция всегда будет равна нулю.

2) Когда $\operatorname{ctg} x < 0$:

• Если $\operatorname{ctg} x < 0$, то $|\operatorname{ctg} x| = -\operatorname{ctg} x$, так как модуль делает отрицательные значения положительными.
• Таким образом, на этих промежутках:

  $$y = -\operatorname{ctg} x — \operatorname{ctg} x = -2 \operatorname{ctg} x.$$

  Это означает, что функция будет отрицательной и удвоенной для значений $\operatorname{ctg} x$ ниже нуля.

3) Область определения:

• Функция $y = \operatorname{ctg} x$ имеет асимптоты в точках $x = n\pi$, где $n \in \mathbb{Z}$.
• Модуль и вычитание $\operatorname{ctg} x$ не изменяют места разрыва функции.
• Таким образом, область определения функции:

  $$x \neq \pi n.$$

4) График функции:

• График функции:
  • Для значений $\operatorname{ctg} x \geq 0$ график будет равен 0.
  • Для значений $\operatorname{ctg} x < 0$ график будет удвоенным отрицательным графиком котангенса.
  • График будет прерываться в точках $x = n\pi$, где $n \in \mathbb{Z}$.