ГДЗ по Алгебре 10 Класс Номер 20.23 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) у = tgx|ctgх|;

б) у = |tgх|ctgx

а) $y = \operatorname{tg} x \cdot |\operatorname{ctg} x|$;

Если $\operatorname{ctg} x \geq 0$, тогда:

$$y = \operatorname{tg} x \cdot \operatorname{ctg} x = 1;$$

Если $\operatorname{ctg} x < 0$, тогда:

$$y = \operatorname{tg} x \cdot (-\operatorname{ctg} x) = -1;$$

Область определения:

$$x_1 \neq \frac{\pi}{2} + \pi n;$$ $$x_2 \neq \pi n;$$

График функции:

б) $y = |\operatorname{tg} x| \cdot \operatorname{ctg} x$;

Если $\operatorname{tg} x \geq 0$, тогда:

$$y = \operatorname{tg} x \cdot \operatorname{ctg} x = 1;$$

Если $\operatorname{tg} x < 0$, тогда:

$$y = -\operatorname{tg} x \cdot \operatorname{ctg} x = -1;$$

Область определения:

$$x_1 \neq \frac{\pi}{2} + \pi n;$$ $$x_2 \neq \pi n;$$

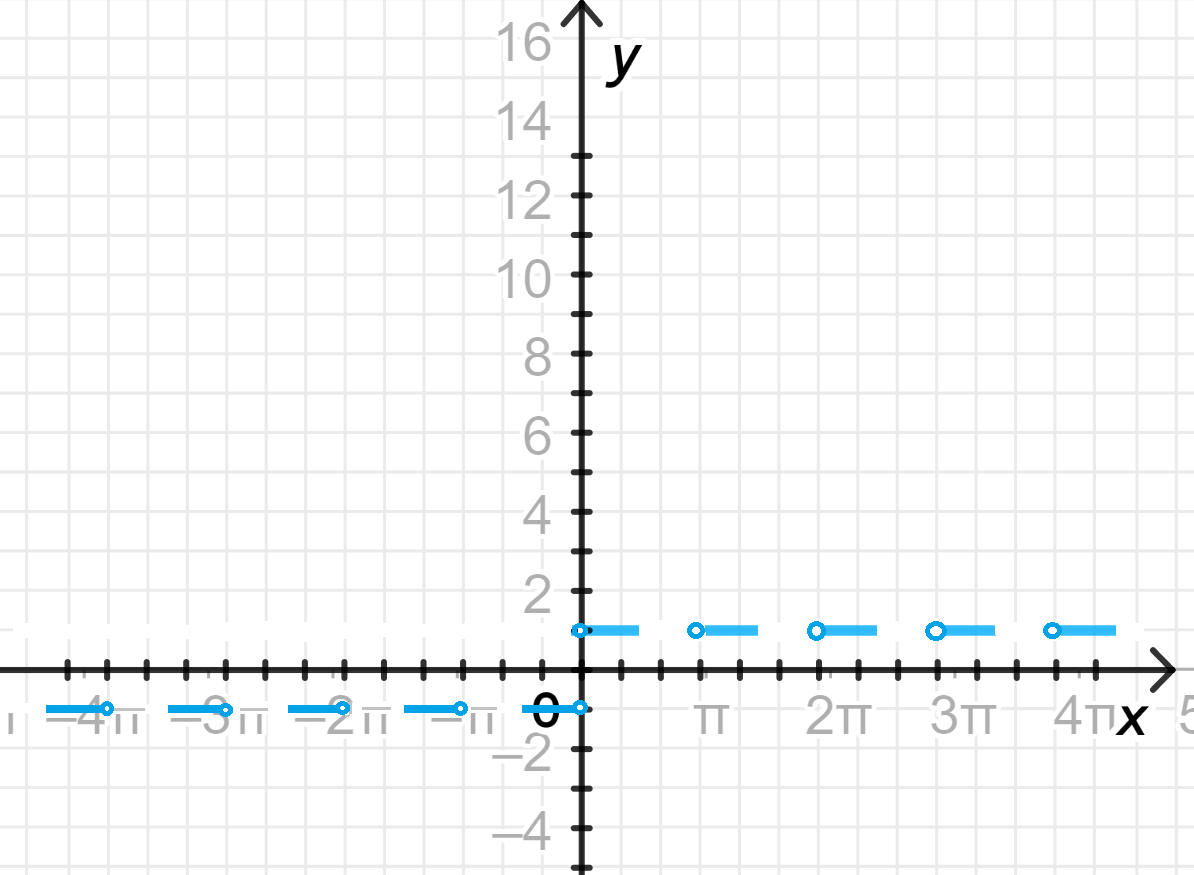
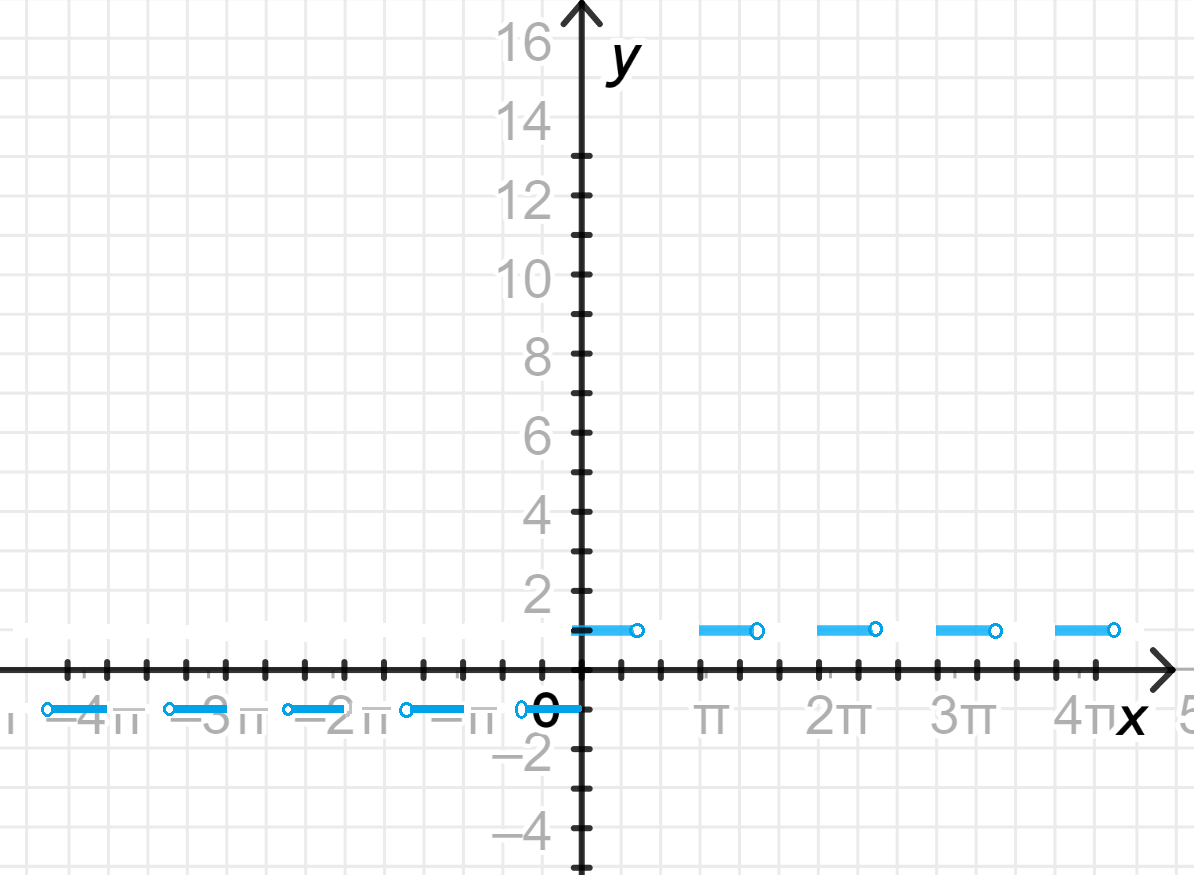
График функции:

а) $y = \operatorname{tg} x \cdot |\operatorname{ctg} x|$

1) Когда $\operatorname{ctg} x \geq 0$:

• Если $\operatorname{ctg} x \geq 0$, то $|\operatorname{ctg} x| = \operatorname{ctg} x$, так как модуль не изменяет положительные значения.
• Тогда функция $y$ принимает вид:

  $$y = \operatorname{tg} x \cdot \operatorname{ctg} x.$$

• С использованием основной тригонометрической идентичности $\operatorname{tg} x \cdot \operatorname{ctg} x = 1$, получаем:

  $$y = 1.$$

  Таким образом, если $\operatorname{ctg} x \geq 0$, функция всегда равна 1.

2) Когда $\operatorname{ctg} x < 0$:

• Если $\operatorname{ctg} x < 0$, то $|\operatorname{ctg} x| = -\operatorname{ctg} x$, так как модуль превращает отрицательные значения в положительные.
• Тогда функция $y$ принимает вид:

  $$y = \operatorname{tg} x \cdot (-\operatorname{ctg} x) = -1.$$

  Таким образом, если $\operatorname{ctg} x < 0$, функция всегда равна -1.

3) Область определения:

• Функция $\operatorname{tg} x$ имеет асимптоты в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
• Функция $\operatorname{ctg} x$ имеет асимптоты в точках $x = \pi n$, где $n \in \mathbb{Z}$.
• Таким образом, область определения функции $y = \operatorname{tg} x \cdot |\operatorname{ctg} x|$ — это все значения $x$, кроме тех, где $\operatorname{tg} x$ и $\operatorname{ctg} x$ имеют асимптоты:

  $$x_1 \neq \frac{\pi}{2} + \pi n, \quad x_2 \neq \pi n.$$

4) График функции:

• Для $\operatorname{ctg} x \geq 0$, функция всегда равна 1.
• Для $\operatorname{ctg} x < 0$, функция всегда равна -1.
• График функции будет постоянным на промежутках между асимптотами:
  • На интервалах, где $\operatorname{ctg} x \geq 0$, график будет равен 1.
  • На интервалах, где $\operatorname{ctg} x < 0$, график будет равен -1.

б) $y = |\operatorname{tg} x| \cdot \operatorname{ctg} x$

1) Когда $\operatorname{tg} x \geq 0$:

• Если $\operatorname{tg} x \geq 0$, то $|\operatorname{tg} x| = \operatorname{tg} x$, так как модуль не изменяет положительные значения.
• Тогда функция $y$ принимает вид:

  $$y = \operatorname{tg} x \cdot \operatorname{ctg} x.$$

• С использованием основной тригонометрической идентичности $\operatorname{tg} x \cdot \operatorname{ctg} x = 1$, получаем:

  $$y = 1.$$

  Таким образом, если $\operatorname{tg} x \geq 0$, функция всегда равна 1.

2) Когда $\operatorname{tg} x < 0$:

• Если $\operatorname{tg} x < 0$, то $|\operatorname{tg} x| = -\operatorname{tg} x$, так как модуль превращает отрицательные значения в положительные.
• Тогда функция $y$ принимает вид:

  $$y = -\operatorname{tg} x \cdot \operatorname{ctg} x = -1.$$

  Таким образом, если $\operatorname{tg} x < 0$, функция всегда равна -1.

3) Область определения:

• Функция $\operatorname{tg} x$ имеет асимптоты в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
• Функция $\operatorname{ctg} x$ имеет асимптоты в точках $x = \pi n$, где $n \in \mathbb{Z}$.
• Таким образом, область определения функции $y = |\operatorname{tg} x| \cdot \operatorname{ctg} x$ — это все значения $x$, кроме тех, где $\operatorname{tg} x$ и $\operatorname{ctg} x$ имеют асимптоты:

  $$x_1 \neq \frac{\pi}{2} + \pi n, \quad x_2 \neq \pi n.$$

4) График функции:

• Для $\operatorname{tg} x \geq 0$, функция всегда равна 1.
• Для $\operatorname{tg} x < 0$, функция всегда равна -1.
• График функции будет постоянным на промежутках между асимптотами:
  • На интервалах, где $\operatorname{tg} x \geq 0$, график будет равен 1.
  • На интервалах, где $\operatorname{tg} x < 0$, график будет равен -1.