ГДЗ по Алгебре 10 Класс Номер 20.24 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x + |x|$;

б) $y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x}$

а) $y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x + |x|$;

Если $x \geq 0$, тогда:
$y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x + x = 2 + x;$

Если $x < 0$, тогда:
$y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x — x = 2 — x;$

Область определения:
$x_1 \neq \frac{\pi}{2} + \pi n;$
$x_2 \neq \pi n;$

График функции:

б) $y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x}$;

Область определения:
$x_1 \neq \frac{\pi}{2} + \pi n;$
$x_2 \neq \pi n;$
$x \geq 0;$

Если $x \geq 0$, тогда:
$y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x} = 1 + \sqrt{x};$

График функции:

а) $y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x + |x|$

1) Когда $x \geq 0$:

• Функция $y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x + |x|$ для $x \geq 0$ примет вид:

  $$y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x + x.$$

• Теперь рассмотрим произведение $\operatorname{tg} x \cdot \operatorname{ctg} x$. Из основной тригонометрической идентичности:

  $$\operatorname{tg} x \cdot \operatorname{ctg} x = 1.$$

• Подставим это в исходное выражение:

  $$y = 2 \cdot 1 + x = 2 + x.$$

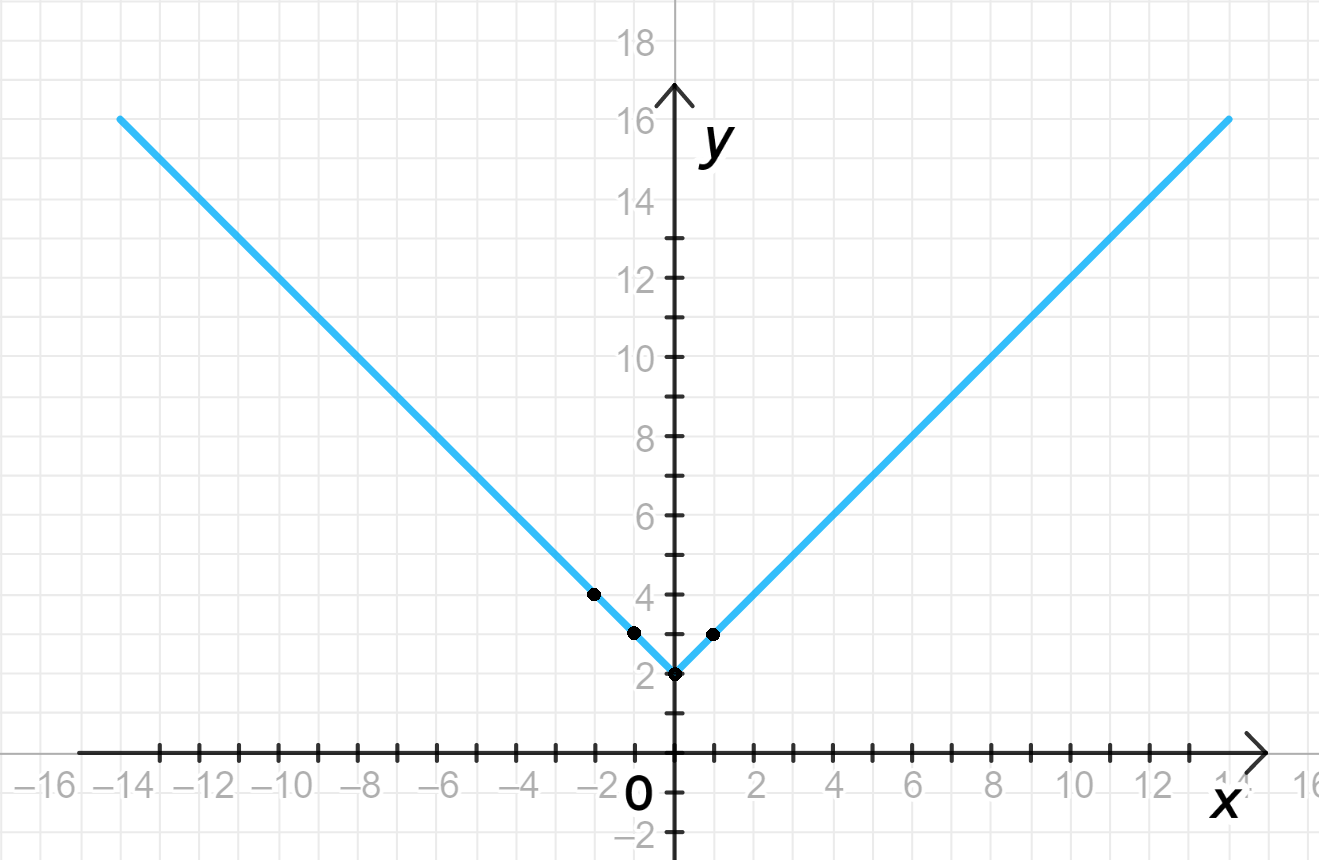
• Таким образом, для $x \geq 0$, функция является линейной и имеет вид $y = 2 + x$. Это функция с углом наклона 1, которая возрастает от точки $(0, 2)$.

2) Когда $x < 0$:

• Для $x < 0$, функция примет вид:

  $$y = 2 \operatorname{tg} x \cdot \operatorname{ctg} x — x.$$

• Аналогично, используя идентичность $\operatorname{tg} x \cdot \operatorname{ctg} x = 1$, получаем:

  $$y = 2 \cdot 1 — x = 2 — x.$$

• Для $x < 0$, функция также линейна, но с углом наклона -1, что означает, что она убывает на интервале $x < 0$ с началом в точке $(0, 2)$.

3) Область определения:

• Функции $\operatorname{tg} x$ и $\operatorname{ctg} x$ имеют асимптоты:
  • $\operatorname{tg} x$ имеет асимптоты в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
  • $\operatorname{ctg} x$ имеет асимптоты в точках $x = \pi n$, где $n \in \mathbb{Z}$.
• Таким образом, область определения функции будет:

  $$x_1 \neq \frac{\pi}{2} + \pi n, \quad x_2 \neq \pi n.$$

4) График функции:

• График функции $y = 2 + x$ для $x \geq 0$ будет линейным с углом наклона 1, проходящим через точку $(0, 2)$.
• График функции $y = 2 — x$ для $x < 0$ будет линейным с углом наклона -1, также проходящим через точку $(0, 2)$.
• Функция будет прервана в точках $x = \frac{\pi}{2} + \pi n$ и $x = \pi n$, где $n \in \mathbb{Z}$.

б) $y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x}$

1) Область определения:

• Как и в предыдущем примере, функции $\operatorname{tg} x$ и $\operatorname{ctg} x$ имеют асимптоты:
  • $\operatorname{tg} x$ имеет асимптоты в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
  • $\operatorname{ctg} x$ имеет асимптоты в точках $x = \pi n$, где $n \in \mathbb{Z}$.
• Однако добавляется функция $\sqrt{x}$, которая определена только для $x \geq 0$.
• Таким образом, область определения функции будет:

  $$x_1 \neq \frac{\pi}{2} + \pi n, \quad x_2 \neq \pi n, \quad x \geq 0.$$

2) Когда $x \geq 0$:

• Для $x \geq 0$, функция примет вид:

  $$y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x}.$$

• С использованием тригонометрической идентичности $\operatorname{tg} x \cdot \operatorname{ctg} x = 1$, получаем:

  $$y = 1 + \sqrt{x}.$$

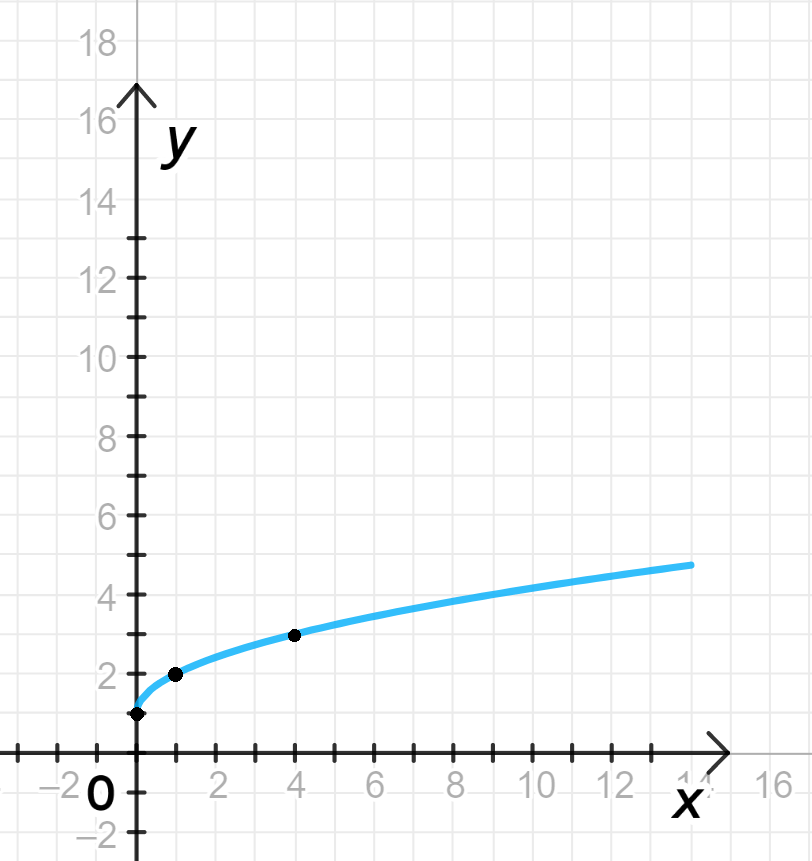
• Это выражение описывает функцию, которая увеличивается с увеличением $x$, начиная от 1 при $x = 0$ и постепенно увеличиваясь. Функция $\sqrt{x}$ имеет характерное замедленное увеличение.

3) График функции:

• График функции $y = 1 + \sqrt{x}$ будет представлять собой кривую, начинающуюся в точке $(0, 1)$ и постепенно увеличивающуюся по мере роста $x$.
• На графике будут асимптоты в точках $x = \frac{\pi}{2} + \pi n$ и $x = \pi n$, где $n \in \mathbb{Z}$.
• Функция будет определена только для $x \geq 0$, и график будет прерываться в этих точках.