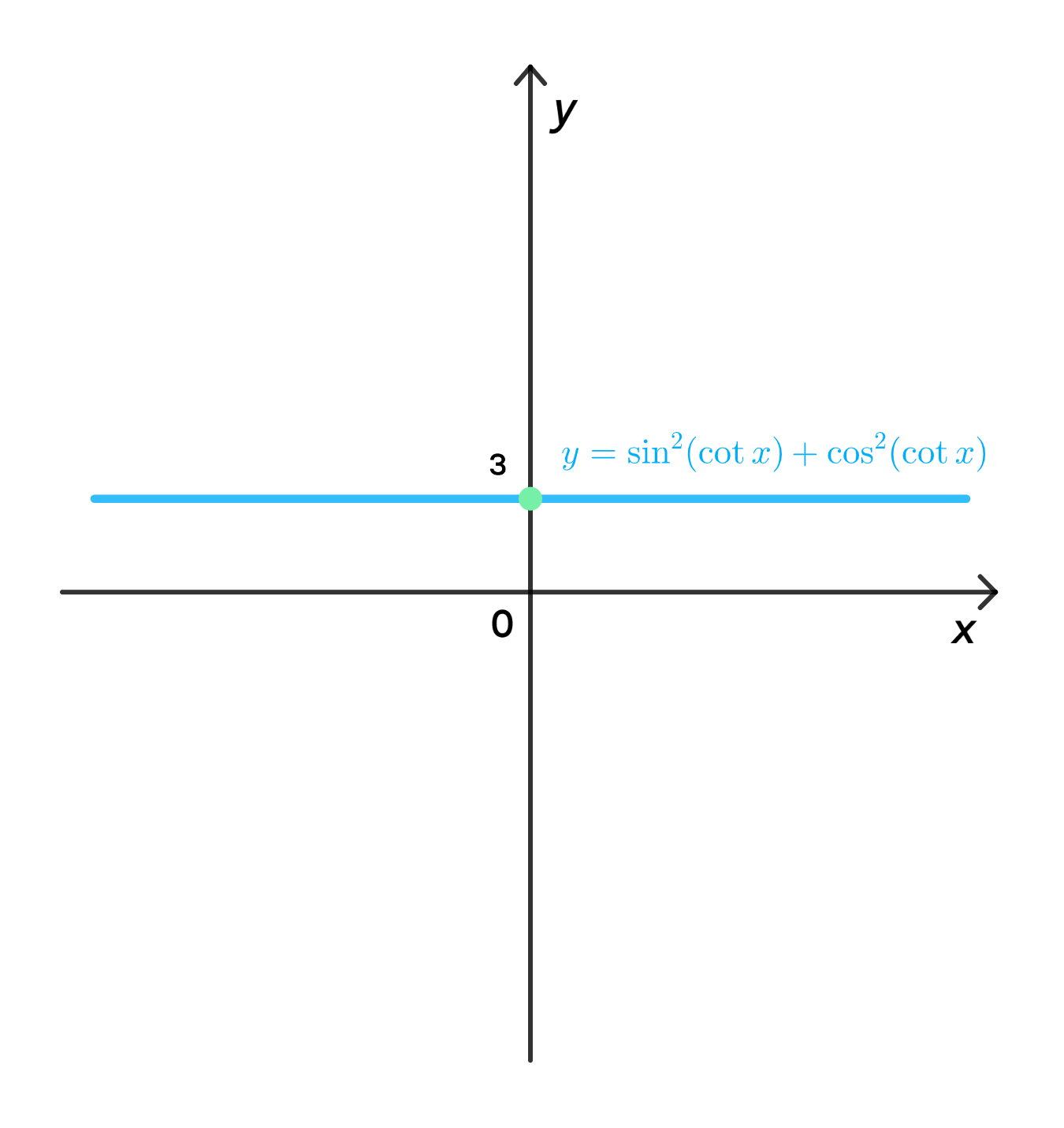ГДЗ по Алгебре 10 Класс Номер 20.25 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

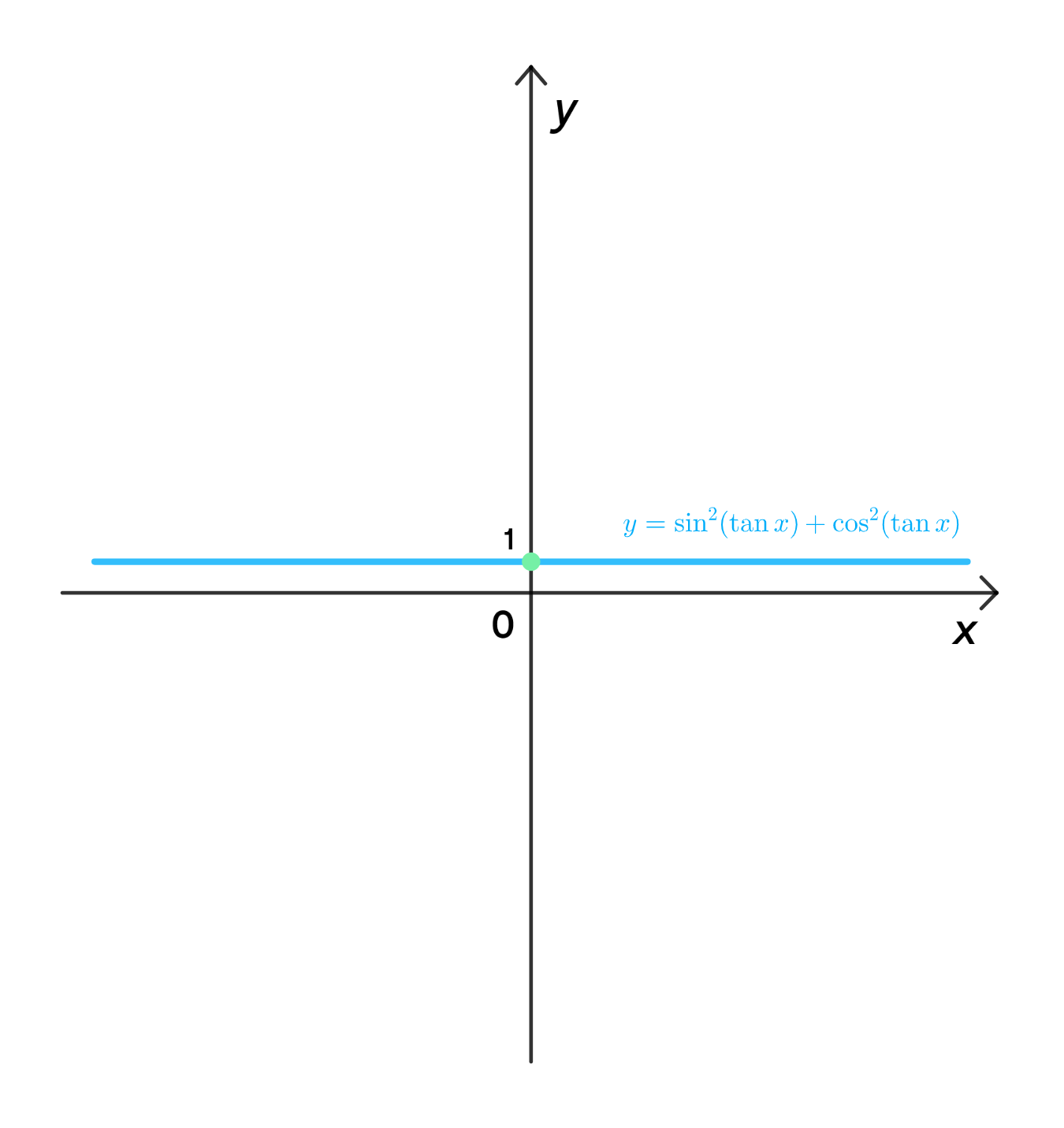
а) у = sin²(tgx) + cos²(tgx);

б) у = 3cos²(ctgx) + 3sin²(ctgx).

а) $y = \sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x) = 1$;

Область определения функции:
$x \neq \frac{\pi}{2} + \pi n;$

График функции:

б) $y = 3 \cos^2(\operatorname{ctg} x) + 3 \sin^2(\operatorname{ctg} x) = 3$;

Область определения функции:
$x \neq \pi n;$

График функции:

а) $y = \sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x) = 1$

1) Рассмотрим тригонометрическую идентичность

• Функция $y = \sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x)$ является выражением для стандартной тригонометрической идентичности:

  $$\sin^2 \theta + \cos^2 \theta = 1.$$

• В нашем случае $\theta = \operatorname{tg} x$, поэтому эта идентичность справедлива для всех значений $x$, где $\operatorname{tg} x$ существует.
• Таким образом, выражение $\sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x)$ всегда равно 1, вне зависимости от значения $x$.

2) Область определения функции

• Функция $\operatorname{tg} x$ имеет асимптоты в точках $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
• Поскольку $\sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x)$ всегда равно 1, это выражение определено на всех значениях $x$, кроме точек, где $\operatorname{tg} x$ не существует, то есть на точках, где $x = \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$.
• Таким образом, область определения функции:

  $$x \neq \frac{\pi}{2} + \pi n.$$

3) График функции

• График функции $y = 1$ будет горизонтальной прямой, так как $y$ всегда равно 1 для любых значений $x$, на которых функция определена.
• График будет прерываться в точках $x = \frac{\pi}{2} + \pi n$, где функция $\operatorname{tg} x$ имеет асимптоты. В этих точках график будет разрываться, так как на этих точках тангенс не существует.

б) $y = 3 \cos^2(\operatorname{ctg} x) + 3 \sin^2(\operatorname{ctg} x) = 3$

1) Рассмотрим тригонометрическую идентичность

• Подобно предыдущему примеру, выражение $3 \cos^2(\operatorname{ctg} x) + 3 \sin^2(\operatorname{ctg} x)$ также является стандартной тригонометрической идентичностью:

  $$\cos^2 \theta + \sin^2 \theta = 1.$$

• В нашем случае $\theta = \operatorname{ctg} x$, поэтому это выражение сводится к:

  $$3 \cdot (\cos^2(\operatorname{ctg} x) + \sin^2(\operatorname{ctg} x)) = 3 \cdot 1 = 3.$$

• Таким образом, выражение $3 \cos^2(\operatorname{ctg} x) + 3 \sin^2(\operatorname{ctg} x)$ всегда равно 3, независимо от значения $x$, где функция $\operatorname{ctg} x$ определена.

2) Область определения функции

• Функция $\operatorname{ctg} x$ имеет асимптоты в точках $x = \pi n$, где $n \in \mathbb{Z}$, поскольку котангенс не существует в этих точках.
• Таким образом, область определения функции:

  $$x \neq \pi n, \quad n \in \mathbb{Z}.$$

3) График функции

• График функции $y = 3$ будет горизонтальной прямой, так как $y$ всегда равно 3 для всех значений $x$, на которых функция определена.
• График будет прерываться в точках $x = \pi n$, где функция $\operatorname{ctg} x$ имеет асимптоты. В этих точках график будет разрываться, так как в этих точках котангенс не существует.