ГДЗ по Алгебре 10 Класс Номер 20.7 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \operatorname{tg}\left(x + \frac{\pi}{2}\right);$

б) $y = \operatorname{tg} x + 1;$

в) $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right);$

г) $y=\mathrm{tg}x-2$$$$$

а) $y = \operatorname{tg}\left(x + \frac{\pi}{2}\right);$

Главная ветвь тангенсоиды имеет центр в точке $\left(-\frac{\pi}{2}; 0\right)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} — \frac{\pi}{2} < x < \frac{\pi}{2} — \frac{\pi}{2};$$ $$-\pi < x < 0;$$

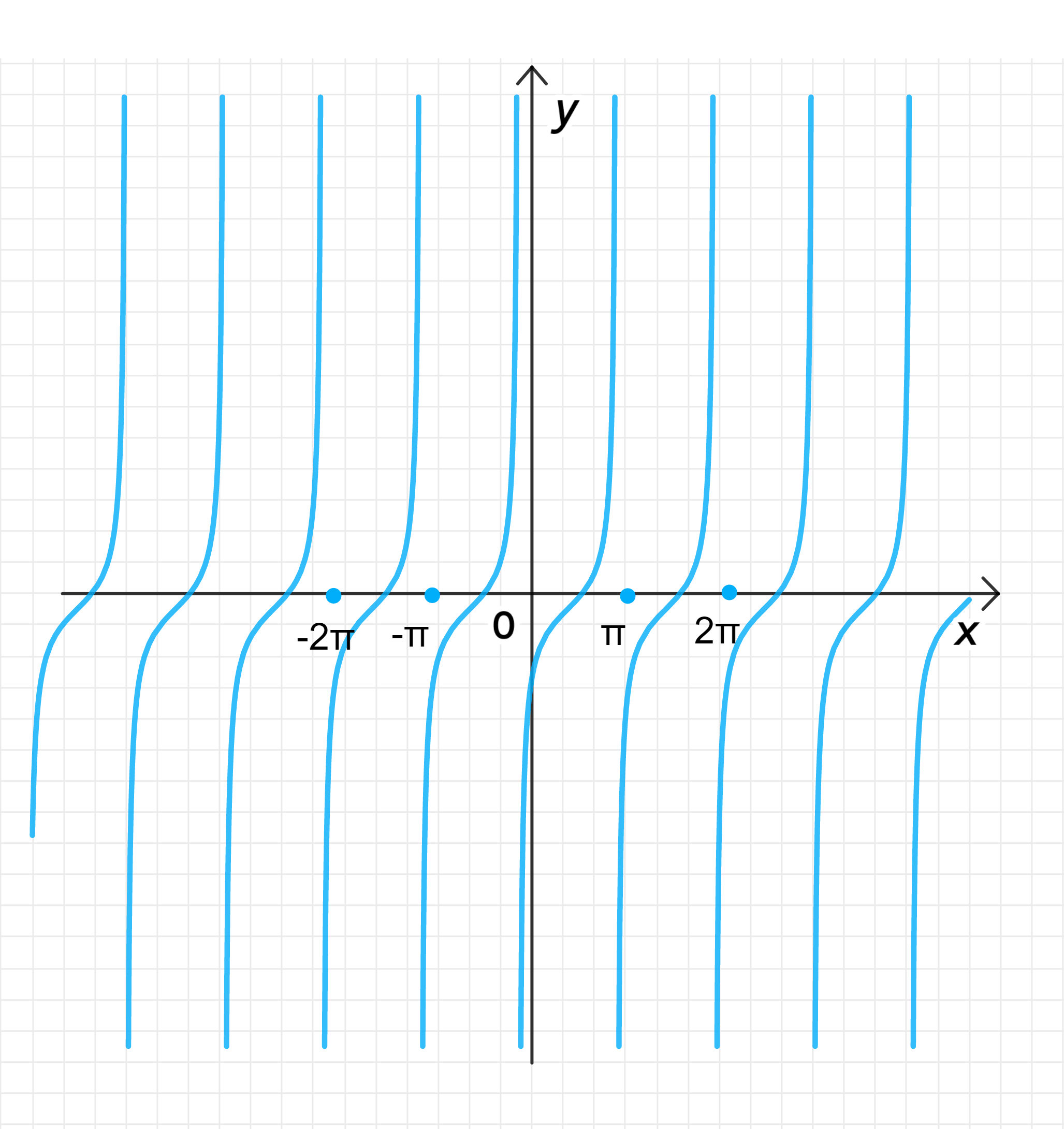
График функции:

б) $y = \operatorname{tg} x + 1;$

Главная ветвь тангенсоиды имеет центр в точке $(0; 1)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} < x < \frac{\pi}{2};$$

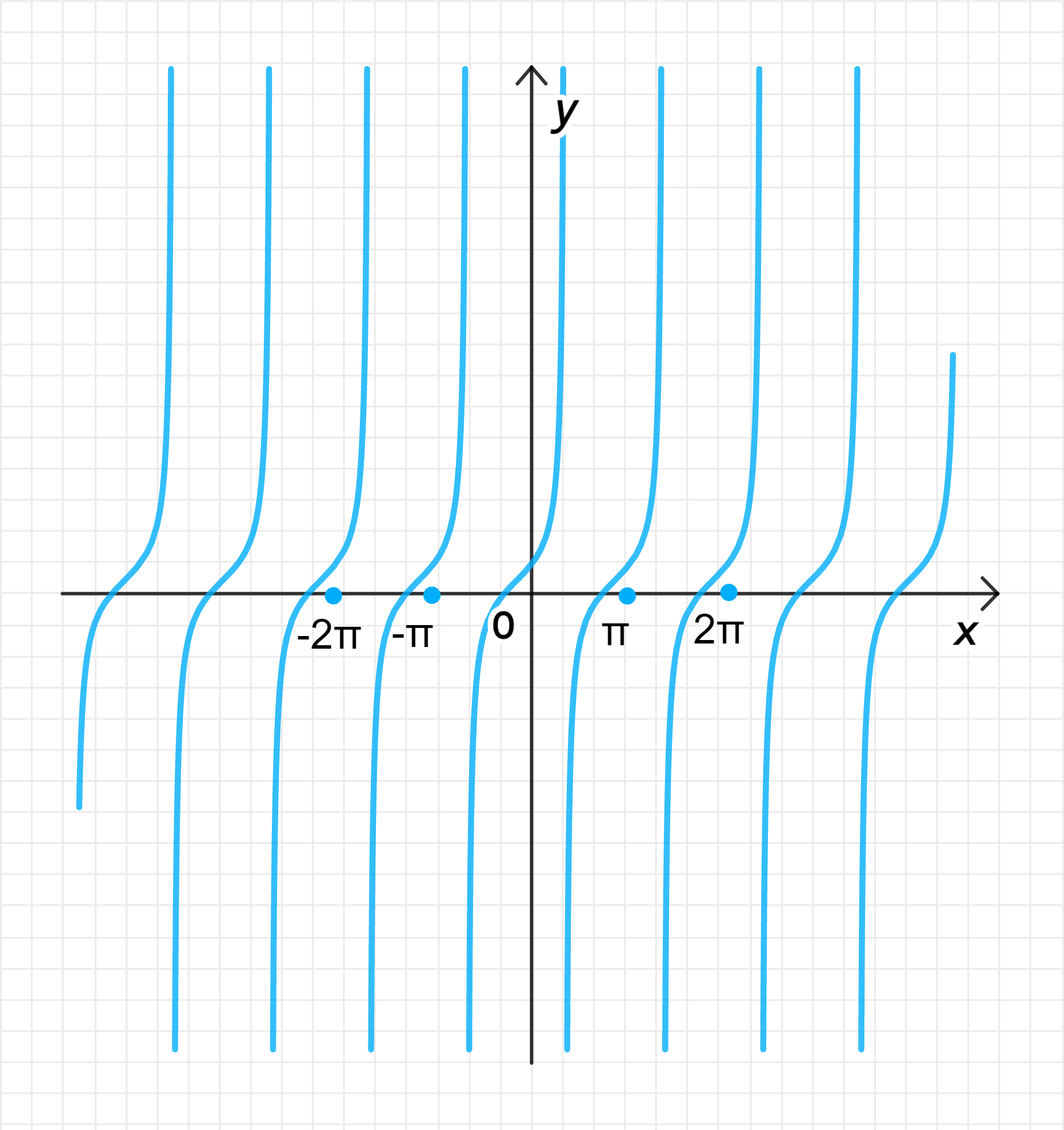
График функции:

в) $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right);$

Главная ветвь тангенсоиды имеет центр в точке $\left(\frac{\pi}{4}, 0\right)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} + \frac{\pi}{4} < x < \frac{\pi}{2} + \frac{\pi}{4};$$ $$-\frac{\pi}{4} < x < \frac{3\pi}{4};$$

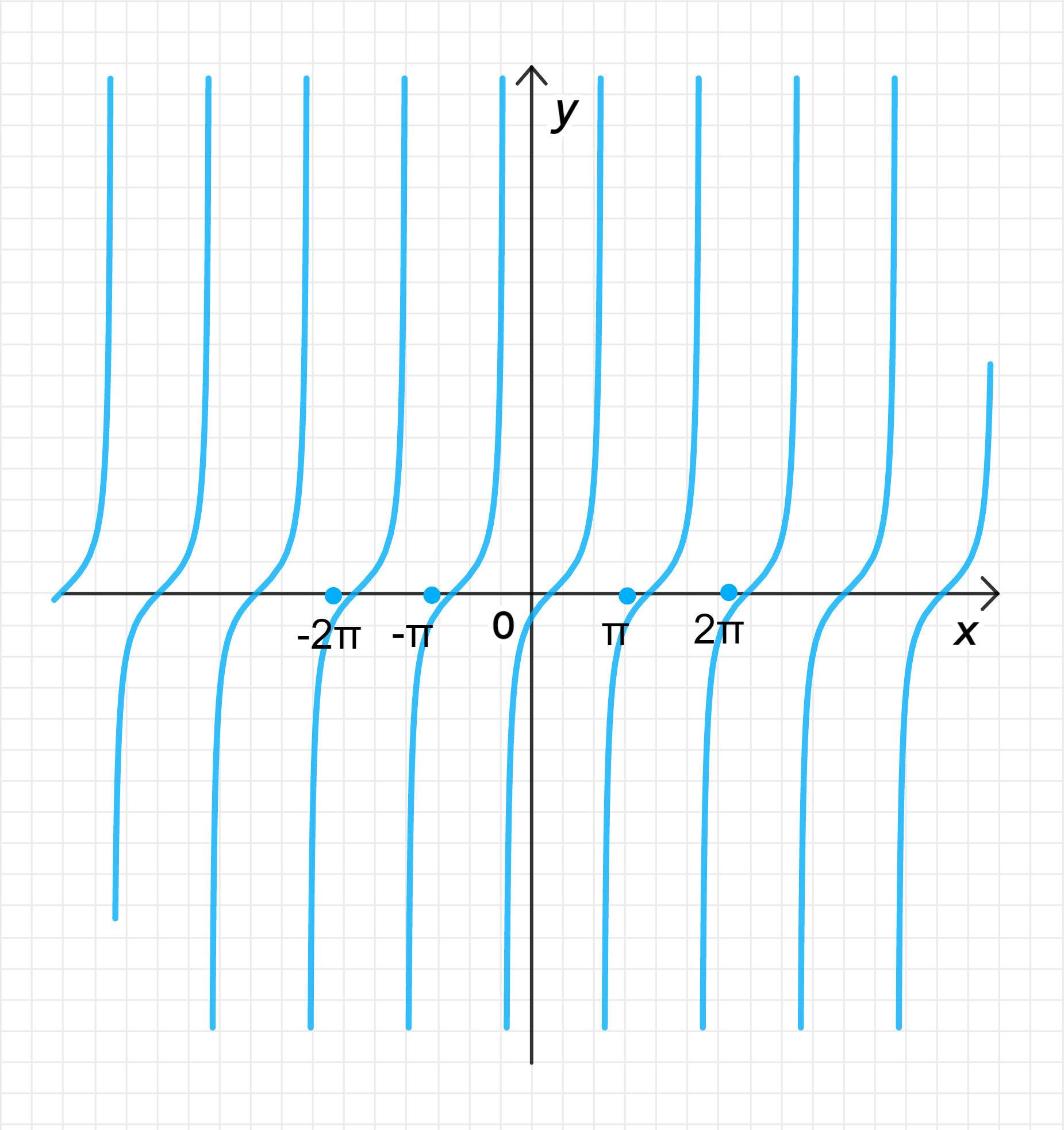
График функции:

г) $y = \operatorname{tg} x — 2;$

Главная ветвь тангенсоиды имеет центр в точке $(0; -2)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} < x < \frac{\pi}{2};$$

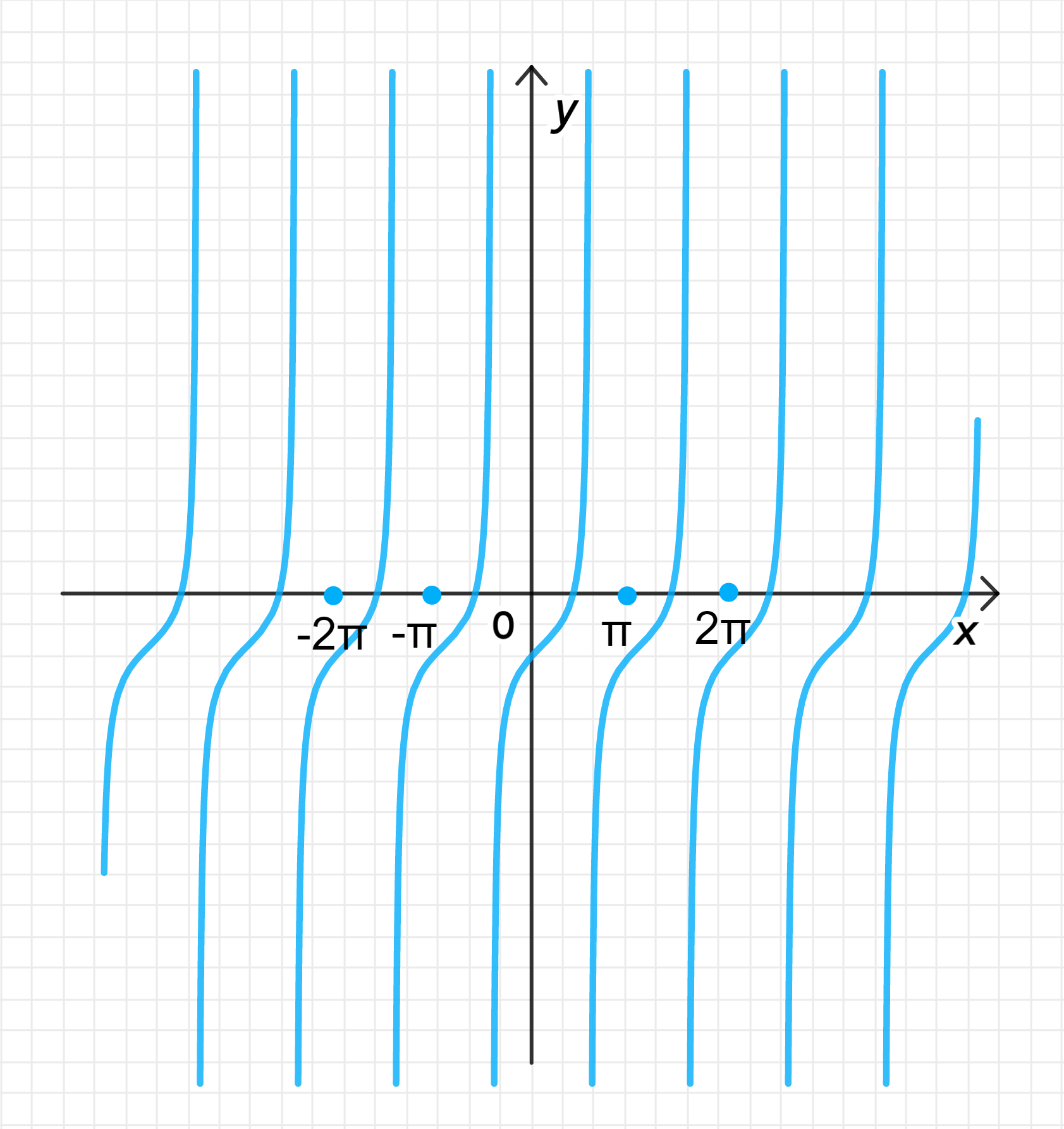
График функции:

Стартовая база: функция $y = \operatorname{tg}(x)$

Перед тем как начать разбирать каждый пример, вспомним ключевые свойства функции $y = \operatorname{tg}(x)$:

• Область определения: $x \ne \frac{\pi}{2} + \pi n$, где $n \in \mathbb{Z}$
• Период: $\pi$
• Центр симметрии (главной ветви): $(0, 0)$
• Главная ветвь: участок графика между двумя вертикальными асимптотами $x = -\frac{\pi}{2}$ и $x = \frac{\pi}{2}$
• Форма графика: непрерывная возрастающая кривая, проходящая через центр симметрии
• Асимптоты: вертикальные прямые, к которым график приближается, но не пересекает

Теперь рассмотрим каждый случай.

а) $y = \operatorname{tg}\left(x + \frac{\pi}{2}\right)$

Шаг 1: Влияние аргумента

Форма:

$$y = \operatorname{tg}(x + a)$$

означает горизонтальный сдвиг графика на $-a$.
В нашем случае $a = \frac{\pi}{2}$, следовательно:

• График $y = \operatorname{tg}(x)$ сдвигается влево на $\frac{\pi}{2}$

Шаг 2: Центр главной ветви

У функции $y = \operatorname{tg}(x)$, центр главной ветви — это точка $(0, 0)$.
После сдвига на $\frac{\pi}{2}$ влево, новый центр:

$$x = 0 — \frac{\pi}{2} = -\frac{\pi}{2} \quad \Rightarrow \quad \text{центр: } \left( -\frac{\pi}{2}, 0 \right)$$

Шаг 3: Интервал главной ветви

Главная ветвь исходной функции находится в интервале:

$$x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$$

Сдвигаем весь интервал влево на $\frac{\pi}{2}$:

$$x \in \left( -\frac{\pi}{2} — \frac{\pi}{2}, \frac{\pi}{2} — \frac{\pi}{2} \right) = \left( -\pi, 0 \right)$$

б) $y = \operatorname{tg}(x) + 1$

Шаг 1: Влияние на график

Форма:

$$y = \operatorname{tg}(x) + b$$

означает вертикальный сдвиг графика на $b$ вверх, если $b > 0$.

Здесь $b = 1$, значит график поднимается на одну единицу по оси $y$.

Шаг 2: Центр главной ветви

У функции $y = \operatorname{tg}(x)$ центр главной ветви:

$$(0, 0) \Rightarrow (0, 0 + 1) = (0, 1)$$

Шаг 3: Интервал главной ветви

Так как аргумент остался $x$, никаких сдвигов по оси $x$ не было.
Значит, интервал остался без изменений:

$$x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$$

в) $y = \operatorname{tg}\left(x — \frac{\pi}{4} \right)$

Шаг 1: Влияние аргумента

Аналогично первому примеру, форма:

$$y = \operatorname{tg}(x — a) \Rightarrow \text{сдвиг вправо на } a$$

Здесь $a = \frac{\pi}{4}$

Шаг 2: Центр главной ветви

Центр $(0, 0)$ сдвигается вправо на $\frac{\pi}{4}$:

$$(0 + \frac{\pi}{4}, 0) = \left( \frac{\pi}{4}, 0 \right)$$

Шаг 3: Интервал главной ветви

Сдвигаем интервал $\left(-\frac{\pi}{2}, \frac{\pi}{2} \right)$ вправо на $\frac{\pi}{4}$:

$$x \in \left( -\frac{\pi}{2} + \frac{\pi}{4}, \frac{\pi}{2} + \frac{\pi}{4} \right) = \left( -\frac{\pi}{4}, \frac{3\pi}{4} \right)$$$x \in \left( -\frac{\pi}{4}, \frac{3\pi}{4} \right)$

г) $y = \operatorname{tg}(x) — 2$

Шаг 1: Влияние на график

Здесь используется форма:

$$y = \operatorname{tg}(x) + b, \quad b = -2 \Rightarrow \text{сдвиг вниз на 2 единицы}$$

Шаг 2: Центр главной ветви

Центр $(0, 0) \rightarrow (0, -2)$

Шаг 3: Интервал главной ветви

Нет изменений аргумента $x$, следовательно:

$$x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$$

$x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$