ГДЗ по Алгебре 10 Класс Номер 20.8 Профильный Уровень Мордкович — Подробные Ответы

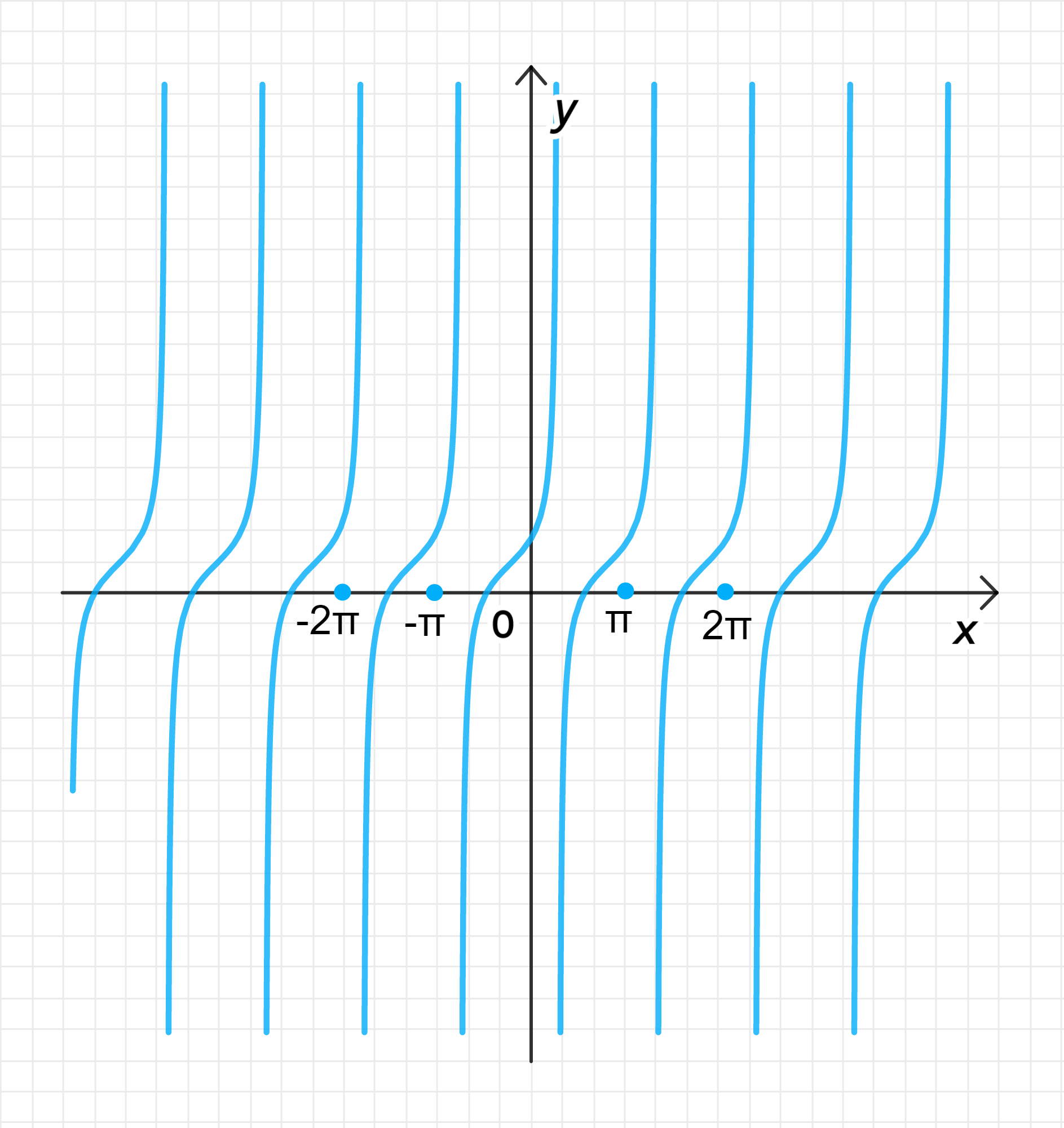
а) $y = \operatorname{tg}\left(x + \frac{\pi}{6}\right) + 1$;

Главная ветвь тангенсоиды имеет центр в точке $\left(-\frac{\pi}{6}; 1\right)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} — \frac{\pi}{6} < x < \frac{\pi}{2} — \frac{\pi}{6};$$ $$-\frac{2\pi}{3} < x < \frac{\pi}{3};$$

График функции:

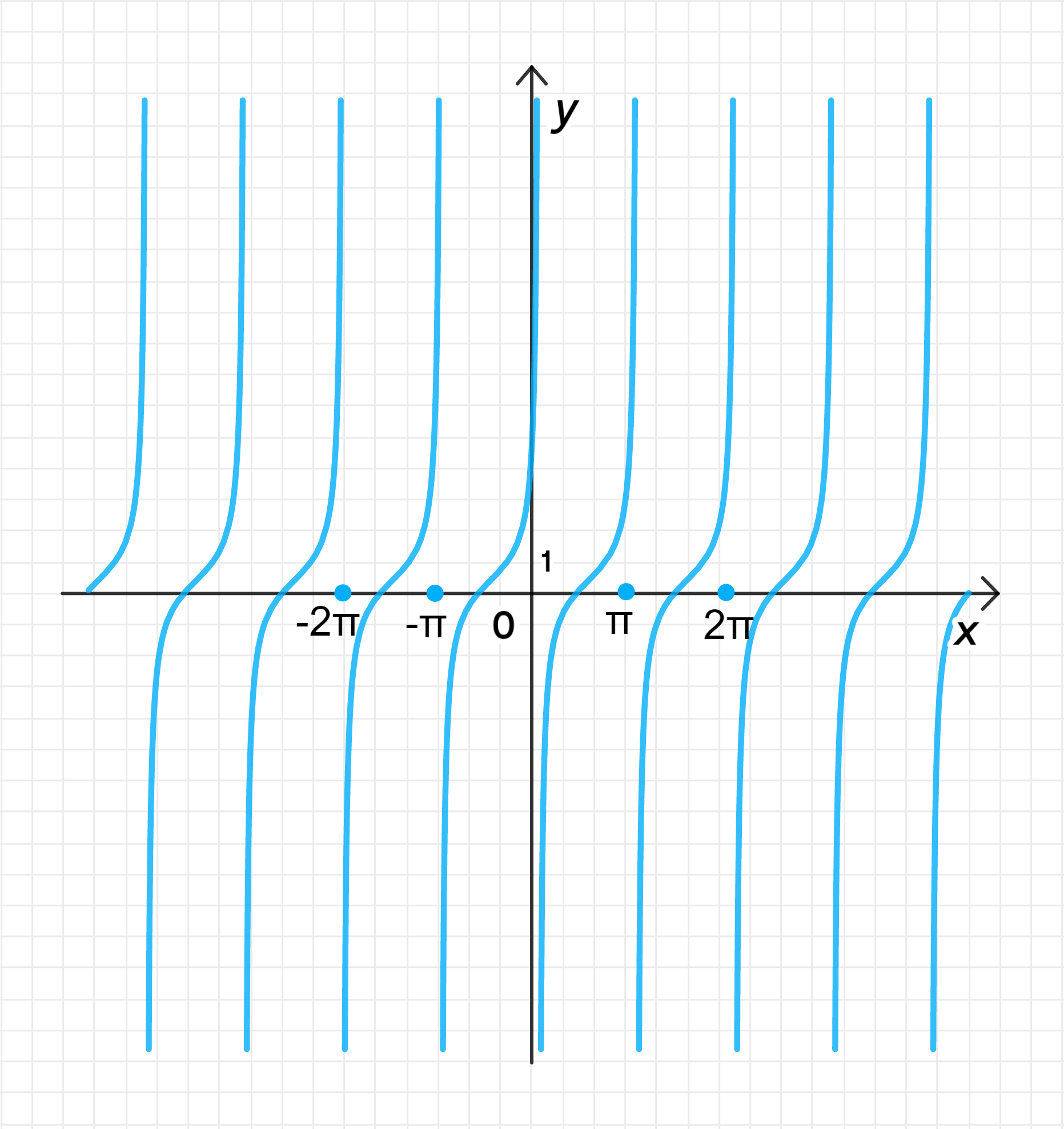
б) $y = \operatorname{tg}\left(x — \frac{2\pi}{3}\right) + \frac{1}{2}$;

Главная ветвь тангенсоиды имеет центр в точке $\left(\frac{2\pi}{3}; \frac{1}{2}\right)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} + \frac{2\pi}{3} < x < \frac{\pi}{2} + \frac{2\pi}{3};$$ $$\frac{\pi}{6} < x < \frac{7\pi}{6};$$

График функции:

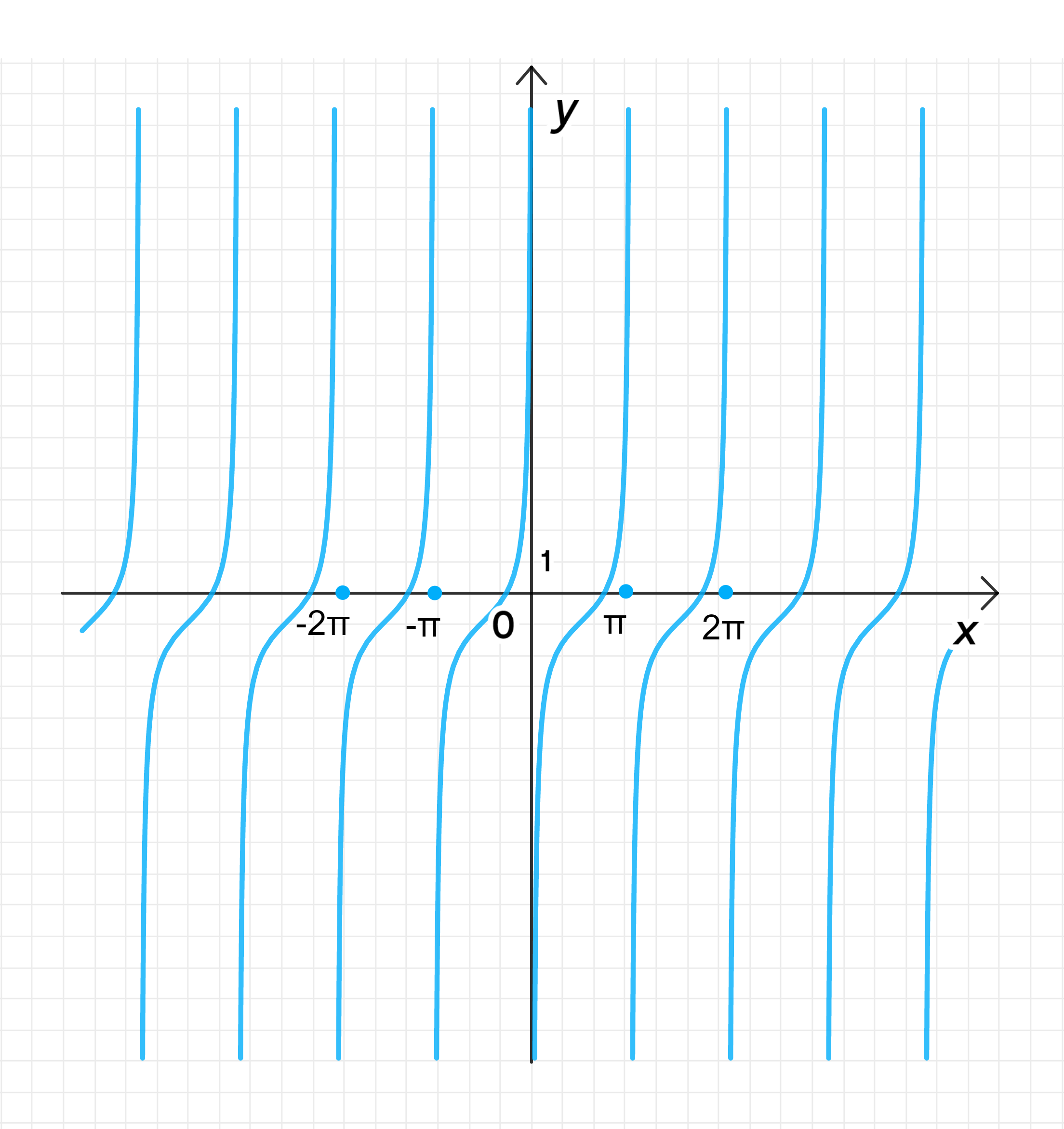
в) $y = \operatorname{tg}\left(x — \frac{\pi}{2}\right) — 1$;

Главная ветвь тангенсоиды имеет центр в точке $\left(\frac{\pi}{2}; -1\right)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} + \frac{\pi}{2} < x < \frac{\pi}{2} + \frac{\pi}{2};$$ $$0 < x < \pi;$$

График функции:

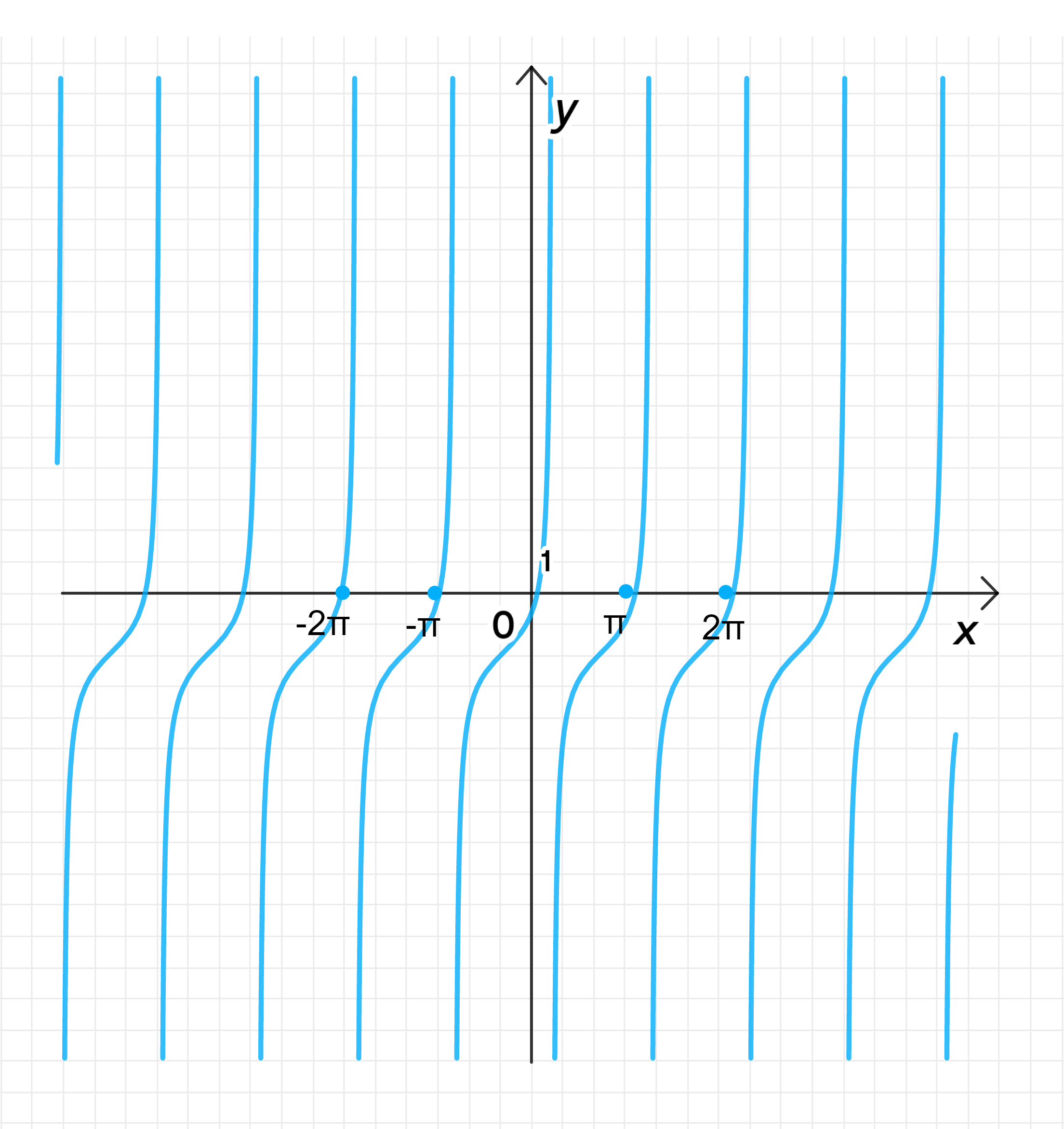
г) $y = \operatorname{tg}\left(x + \frac{\pi}{3}\right) — 2$;

Главная ветвь тангенсоиды имеет центр в точке $\left(-\frac{\pi}{3}; -2\right)$;

Ветвь лежит на интервале:

$$-\frac{\pi}{2} — \frac{\pi}{3} < x < \frac{\pi}{2} — \frac{\pi}{3};$$ $$-\frac{5\pi}{6} < x < \frac{\pi}{6};$$

График функции:

а) $y = \operatorname{tg}\left(x + \frac{\pi}{6}\right) + 1$

Шаг 1: Общий вид функции

Функция имеет вид:

$$y = \operatorname{tg}(x + a) + b$$

где:

• $a = \frac{\pi}{6}$ — сдвиг по оси x (влево);
• $b = 1$ — сдвиг по оси y (вверх).

Шаг 2: Центр главной ветви

Центр главной ветви тангенсоиды — это точка, в которой аргумент тангенса равен нулю:

$$x + \frac{\pi}{6} = 0 \Rightarrow x = -\frac{\pi}{6}$$

Теперь прибавим вертикальный сдвиг:

$$y = \operatorname{tg}(0) + 1 = 0 + 1 = 1$$

Центр: $\left( -\frac{\pi}{6}; 1 \right)$

Шаг 3: Интервал главной ветви

Основной интервал тангенсоиды без сдвига:

$$-\frac{\pi}{2} < x < \frac{\pi}{2}$$

Теперь заменим $x$ на $x + \frac{\pi}{6}$:

$$-\frac{\pi}{2} < x + \frac{\pi}{6} < \frac{\pi}{2}$$

Вычитаем $\frac{\pi}{6}$ из всех частей неравенства:

$$-\frac{\pi}{2} — \frac{\pi}{6} < x < \frac{\pi}{2} — \frac{\pi}{6}$$

Приводим к общему знаменателю:

$$-\frac{2\pi}{3} < x < \frac{\pi}{3}$$

Шаг 4: График

б) $y = \operatorname{tg}\left(x — \frac{2\pi}{3}\right) + \frac{1}{2}$

Шаг 1: Общий вид

Форма та же: $y = \operatorname{tg}(x — a) + b$

• Горизонтальный сдвиг вправо на $\frac{2\pi}{3}$;
• Вертикальный сдвиг вверх на $\frac{1}{2}$.

Шаг 2: Центр главной ветви

$$x — \frac{2\pi}{3} = 0 \Rightarrow x = \frac{2\pi}{3}$$ $$y = \operatorname{tg}(0) + \frac{1}{2} = 0 + \frac{1}{2} = \frac{1}{2}$$

Центр: $\left( \frac{2\pi}{3}; \frac{1}{2} \right)$

Шаг 3: Интервал

Начнем с:

$$-\frac{\pi}{2} < x — \frac{2\pi}{3} < \frac{\pi}{2}$$

Прибавим $\frac{2\pi}{3}$ к каждой части:

$$-\frac{\pi}{2} + \frac{2\pi}{3} < x < \frac{\pi}{2} + \frac{2\pi}{3}$$

Приводим к общему знаменателю:

$$\frac{-3\pi + 4\pi}{6} = \frac{\pi}{6}, \quad \frac{3\pi + 4\pi}{6} = \frac{7\pi}{6}$$ $$\frac{\pi}{6} < x < \frac{7\pi}{6}$$

Шаг 4: График

в) $y = \operatorname{tg}\left(x — \frac{\pi}{2}\right) — 1$

Шаг 1: Вид

Функция: $y = \operatorname{tg}(x — a) + b$

• Горизонтальный сдвиг вправо на $\frac{\pi}{2}$;
• Вертикальный сдвиг вниз на 1.

Шаг 2: Центр

$$x — \frac{\pi}{2} = 0 \Rightarrow x = \frac{\pi}{2}$$ $$y = \operatorname{tg}(0) — 1 = 0 — 1 = -1$$

Центр: $\left( \frac{\pi}{2}; -1 \right)$

Шаг 3: Интервал

$$-\frac{\pi}{2} < x — \frac{\pi}{2} < \frac{\pi}{2}$$

Прибавим $\frac{\pi}{2}$:

$$0 < x < \pi$$

Шаг 4: График

г) $y = \operatorname{tg}\left(x + \frac{\pi}{3}\right) — 2$

Шаг 1: Форма

$y = \operatorname{tg}(x + a) + b$

• Сдвиг влево на $\frac{\pi}{3}$;
• Сдвиг вниз на 2.

Шаг 2: Центр

$$x + \frac{\pi}{3} = 0 \Rightarrow x = -\frac{\pi}{3}$$ $$y = \operatorname{tg}(0) — 2 = -2$$

Центр: $\left( -\frac{\pi}{3}; -2 \right)$

Шаг 3: Интервал

$$-\frac{\pi}{2} < x + \frac{\pi}{3} < \frac{\pi}{2}$$

Вычтем $\frac{\pi}{3}$:

$$-\frac{\pi}{2} — \frac{\pi}{3} < x < \frac{\pi}{2} — \frac{\pi}{3}$$ $$-\frac{3\pi + 2\pi}{6} = -\frac{5\pi}{6}, \quad \frac{3\pi — 2\pi}{6} = \frac{\pi}{6}$$ $$-\frac{5\pi}{6} < x < \frac{\pi}{6}$$

Шаг 4: График